Conseil :
Tu peux utiliser l'espace en bas ou à côté de chaque exercice pour mettre tes réponses
Exercice 1
Soit un segment [AB] et I son milieu.
1. Comment sont disposés les points A, I et B.
2. Compare les longueurs AI et IB.
3. Quelle est l'image de I par la translation qui transforme A en I ?
Exercice 2
1. Trace deux droites (D) et (D') parallèles puis marque deux points A et B sur (D) et un point C sur (D').
2. Construis le point C' tel que ABC'C soit un parallélogramme
3. Quelle translation transforme C en C'?
Exercice 3
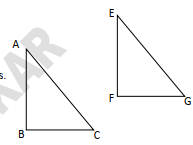
Dans la figure ci-contre, ABC et EFG sont deux triangles rectangles de mêmes dimensions, (AB) et (EF) sont parallèles.
Quelle est l'image de chacun des points E, F et G par la translation qui transforme G en C ?
Exercice 4
Répond par vrai ou faux à chacune des affirmations ci-dessous :
Soit un vecteur \(\overrightarrow{\rm EF}\) et O un point du plan.
1. Si \(\overrightarrow{\rm OE} = \overrightarrow{\rm FE}\) alors O est le milieu du segment [EF].
2. Si \(\overrightarrow{\rm EO} = \overrightarrow{\rm OF}\) alors O est le milieu du segment [EF].
3. Si \(\overrightarrow{\rm EO} = \overrightarrow{\rm FO}\) alors O est le milieu du segment [EF].
4. Si \(\overrightarrow{\rm OE} = \overrightarrow{\rm OF}\) alors O est le milieu du segment [EF].
Exercice 5
\(\overrightarrow{\rm U}\) est un vecteur donné et E un point du plan.
1. Construis les points N et M tel que\( \overrightarrow{\rm U}= \overrightarrow{\rm EN}\) et \(\overrightarrow{\rm EN}= \overrightarrow{\rm NM}\)
2. Justifie que N est le milieu du segment [EM]
Exercice 6
Soit E, F et G trois points non alignés du plan
1. Construis les points M et N tel que\( \overrightarrow{\rm EM}= \overrightarrow{\rm FG}\) et \(\overrightarrow{\rm EN}= \overrightarrow{\rm GF}\)
2. Justifie que E est le milieu du segment [NM]
Exercice 7
Recopie puis complète les phrases ci-dessous.
1. Si trois points sont alignés alors leurs images par une translation ............
2. L'image d'un segment par une translation est un segment.....................
3. L'image d'une droite par une translation est une droite..................
4. L'image d'un cercle par une translation est un cercle de.................. et ...............
5. L'image d'un angle par une translation est un ......................
Exercice 8
ABC est un triangle rectangle en A tel que AB = 5 cm et AC = 4 cm. Soit I le milieu de [BC]
1. Construis les points B' C'et I' images respectives des points B, C et I par la translation qui transforme A en C.
2. Quelle est la longueur du segment [B'C'] ? Justifie.
3. Quelle est la position des trois points A', B' et C' ? Justifie.
4. Quelle est la mesure de l'angle \(\widehat{B'CC'}\) ? Justifie
Exercice 9
Soit le cercle C(O,3 cm).
1. Marque un point M sur le cercle et un point N à l'extérieur du cercle.
2. Construis les points O' et M' images respectives des points O et M par la translation qui transforme M en N.
3. Construis le cercle (C') de centre O' et de rayon O'M'.
4. Montre que (C') est l'image de (C) par la translation qui transforme M en N.
Exercice 10
Répond par vrai ou faux à chacune des affirmations ci-dessous.
1. Si ABCD est un parallélogramme alors \( \overrightarrow{\rm AB}= \overrightarrow{\rm CD}\)
2. Si ABCD est un parallélogramme alors \( \overrightarrow{\rm AD}= \overrightarrow{\rm BC}\)
3. Si ABCD est un parallélogramme alors \( \overrightarrow{\rm AC}= \overrightarrow{\rm BD}\)
4. Si ABCD est un parallélogramme alors \( \overrightarrow{\rm DA}= \overrightarrow{\rm BC}\)
5. Si ABCD est un parallélogramme alors \( \overrightarrow{\rm CD}= \overrightarrow{\rm BA}\)
Exercice 11
1. Construis un triangle EFG, puis les points H, A, B tel que :
H pied de la hauteur issue de E ;
A l'image de E par la translation de vecteur \(\overrightarrow{\rm HF}\) ;
B l'image de E par la translation de vecteur \( \overrightarrow{\rm HG}\) ;
2. Donne la nature des quadrilatères BEHG et HFAE. Justifie
Exercice 12
1. Construis un cercle C (O ; 3 cm).
2. Marque les points I, J et K sur (C) tels que les points I et J soient diamétralement opposés.
3. Construis le point A l'image de K par la translation de vecteur \(\overrightarrow{\rm JI}\)
4. Quelle est la nature du quadrilatère AIJK ?Justifie
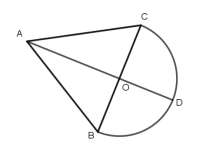
Exercice 13
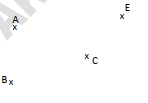
Reproduis la figure ci- contre puis construis:
Le point B' image de B par la translation qui transforme A en C;
Le point C' image de C par la translation qui transforme E en A
Exercice 14
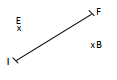
Reproduis la figure ci- contre puis construis l'image du segment [IF] par la translation qui transforme E en B.
Exercice 15
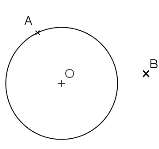
Reproduis la figure ci- contre puis construis l'image du cercle (C) de centre O et de rayon 3 cm par la translation qui transforme B en D.
Exercice 16
Reproduis la figure ci- contre puis construis l'image (D') de la droite (D) par la translation qui transforme A en B.
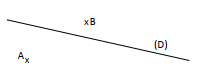
Exercice 17
Reproduis la figure ci- contre puis construis l'image A'B'C' du triangle ABC par la translation qui transforme A en E
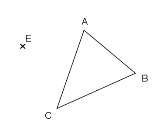
Exercice 18
Dans la figure (F) ci-contre, ABC est un triangle équilatéral et O est le centre du demi-cercle de diamètre [BC].
1. Reproduis la figure (F)
2. Construis l'image (F') de (F) par la translation de vecteur \( \overrightarrow{\rm DA}.\)
3. Justifie que A', O' et D'image de A, O et D par cette translation de vecteur \(\overrightarrow{\rm DA}\) sont align
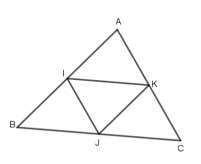
Exercice 19
Dans la figure ci-contre ABC est un triangle et I, J et K les milieux respectifs des segments [AB], [BC] et [CA].
1. Reproduis la figure.
2. Ecris tous les vecteurs qui sont égaux au vecteur \(\overrightarrow{\rm AI}\)
3. Ecris tous les vecteurs qui sont égaux au vecteur \(\overrightarrow{\rm IK}\)
Exercice 20
Pour chacun des énoncés ci-dessous, trois réponses a, b et c sont données dont une seule est juste.
Écris le numéro de l'énoncé et la réponse choisie
N° | Énoncé | a | b | c |
|---|---|---|---|---|
1 | Si ABCD est un parallélogramme alors | \(\overrightarrow{\rm AB}= \)\(\overrightarrow{\rm CD}\) | \(\overrightarrow{\rm BC}= \)\(\overrightarrow{\rm AD}\) | \(\overrightarrow{\rm AC}= \)\(\overrightarrow{\rm BD}\) |
2 | Si le point M est l'image de B par la translation de vecteur alors \(\overrightarrow{\rm AB}\) alors | A est milieu de [MB] | B est milieu de [AM] | M est milieu de [AB] |
3 | Si F est milieu de [EG] alors | \(\overrightarrow{\rm EF}= \)\(\overrightarrow{\rm GF}\) | \(\overrightarrow{\rm EF}= \)\(\overrightarrow{\rm FG}\) | \(\overrightarrow{\rm EG}= \)\(\overrightarrow{\rm GF}\) |
Exercice 21
Soit ABCD un parallélogramme et E un point du plan.
1. Construis le point F tel que \(\overrightarrow{\rm EF} =\overrightarrow{\rm AB}\)
2. Démontre que EFCD est un parallélogramme
Exercice 22
1. Trace un triangle ABC.
2. Construis le point F tel que BCFA soit un parallélogramme.
3. Construis le point H de façon que A soit le milieu de [HB].
4. Démontre que AHFC est un parallélogramme.
Exercice 23
Soit un carré ABCD de centre O et de côté 4 cm. Soit t la translation de vecteur \(\overrightarrow{\rm BO}\)
1. Fais la figure et construis les points E, F, G et H images respectives des points A, B, C et H par t.
2. Démontre que EFGH est carré.
Exercice 24
Soit A, F, G trois points d'une droite (D) et E un point n'appartenant pas à (D).
1. Construis les points M, N images respectives des points F et G par la translation de vecteur \(\overrightarrow{\rm AE}\)
2. Démontre que les points E, M et N sont alignés
Exercice 25
Soit ABC est un triangle rectangle en A et E et F deux points distincts.
1) Construis l'image A'B'C' du triangle ABC par la translation de vecteur \(\overrightarrow{\rm EF}\)
2) Quelle est la nature du triangle A'B'C' ? Justifie.