Conseil :
Tu peux utiliser l'espace en bas ou à côté de chaque exercice pour mettre tes réponses
Exercice 1
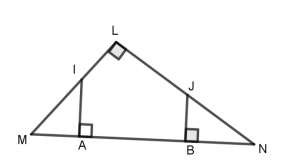
On considère la figure ci-contre. Réponds par vrai ou faux à chacune des affirmations suivantes :
1.I est le projeté orthogonal de A sur (LM).
2.B est le projeté orthogonal de A sur (BJ).
3.L est le projeté orthogonal de M sur (LN).
4. L est le projeté orthogonal de N sur (LM).
5. A est le projeté orthogonal de N sur (IA)
Exercice 2
Dans un triangle ABC, on appelle A' le pied de la hauteur issue de A.
Recopie puis complète la phrase ci-dessous.
Le point ......... est le projeté .......... du point ........... sur............. .
Exercice 3
Trace une droite (D) et marque des points A, B , C n'appartenant pas à (D) et un point E appartenant à (D).
Construis les points A', B', C' et E' projetés orthogonaux respectifs de A, B , C et E sur (D).
Exercice 4
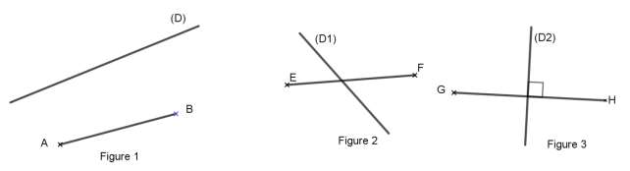
Pour chacune des figures ci-dessous, une droite et un segment sont donnés.
Reproduis chaque figure et construis le projeté orthogonal du segment sur la droite.
Exercice 5
Soit ABC un triangle rectangle en A.
1. a. Quel est le projeté orthogonal de B sur (BC) ?
b. Quel est le projeté orthogonal de C sur (AB) ?
2.a. Marque le point H, projeté orthogonal de A sur (BC).
b. Que représente [AH] pour le triangle ABC ?
3. a. Quel est le projeté orthogonal de [AC] sur (BC) ?
b. Quel est le projeté orthogonal de [AB] sur (BC) ?
Exercice 6
1. Trace un triangle MNP, place A milieu de [MN], puis le point C, pied de la hauteur issue de N.
2. Construis le projeté orthogonal B de A sur (MP).
3. Démontre que B est le milieu de [MC].
Exercice 7
1. Trace un parallélogramme ABCD de centre O.
2. Construis les points E et F, projetés orthogonaux respectifs de A et C sur (BD).
G et H, projetés orthogonaux respectifs de B et D sur (AC).
Quelle est la nature du quadrilatère EGFH ? Justifie.
Exercice 8
Soit ENS un triangle isocèle en E ; I est le milieu du segment [EN], K milieu de [NS] et J le projeté orthogonal de I sur la droite (NS).
Démontre que : NJ=\(\frac 1 4\) NS.
Exercice 9
Le plan est muni d'un repère orthonormal (O, I, J).
1. Place les points A (-2 ; 1) ; B (2 ; 3) ; C (2 ; 0) et D (-2 ; -2).
2. Calcule les coordonnées de E milieu [AC] et F milieu de [DB].
3. Quelle est la nature du quadrilatère ABCD ? Justifie.
Exercice 10
Dans chacun des cas ci-dessous, calcule les coordonnées de R milieu du segment [AB].
1- A (-3 ; 0) et B (5 ; 2) ;
2- A (-2 ; 2) et B (4 ; 0) ;
3- A (\(\frac2 3\) ; -2) et B (3 ; \( \frac 3 2\) )
4- A (− \(\frac 1 2\) ; \(\frac 2 3\) ) et B (\(\frac 1 3\) ;−\(\frac 1 2\) )
Exercice 11
Dans le plan muni d'un repère orthonormal (O; I; J) on donne les points A (-2 ; 4) B (7 ; 2) C (5 ; -7) et D (-4 ; -5).
1. Calcule AB² ; BC² ; CD² ; AD² et BD²
2. Montre que le triangle ABD est rectangle en A.
3. Quelle est la nature du quadrilatère ABCD ?
Exercice 12
Le plan est muni d'un repère orthonormal (O; I; J). On donne A (-2 ; 4) ; B (-2 ; - 4) ; C (2 ; 0).
1. Place les points A ; B et C.
2. Calcule les distances : AB2 ; AC2 et BC2, en déduis la nature du triangle ABC ?
3. Calcule les coordonnées de E centre du cercle (C ) circonscrit à ABC.
Exercice 13
Le plan est muni d'un repère orthonormé (O; I; J). On donne
1. Place les points A (0 ; -1) ; B (3 ; 1); C (1; 4) et M (2; \(\frac 5 2\) ).
2. Démontre que M est le milieu de [BC].
3. Montre que ABC est un triangle rectangle et isocèle en B.
4. Démontre que : BM²=\( \frac 1 4\) A²B2.
5. Détermine les coordonnées du point I centre du cercle circonscrit au triangle ABC.
Exercice 14
Le plan est muni d'un repère orthonormal (O, I, J). on donne les points V (-3 ; 3), A (3 ; 5) et S(5 ;-1)
1. Détermine la nature du triangle VAS.
2. Soit B le milieu de [VS] et E le symétrique de A par rapport à B.
a. Calcule les coordonnées de B et E.
b. Démontre que le quadrilatère VASE est un carré.