Conseil :
Tu peux utiliser l'espace en bas ou à côté de chaque exercice pour mettre tes réponses
Exercice 1
1. Trace le cercle(C) de centre O et de rayon 4cm puis marque 4 points A, B, C et D du cercle.
2. Cite un angle au centre qui intercepte l'arc \(\overset{\displaystyle\frown}{AB}\)
3. Cite deux angles au centre et l'arc intercepté par chacun d'eux
Exercice 2
Soit (C) un cercle de centre O et de rayon R. A et B deux points de (C).
Dans chacun des cas ci-dessous calcule la longueur de l'arc \(\overset{\displaystyle\frown}{AB}\)
1. R=3 cm , \(\widehat{𝐴𝑂𝐵}\) = 60°.
2. R=3 cm , \(\widehat{𝐴𝑂𝐵}\) = 45°.
3. R=4,5 cm , \(\widehat{𝐴𝑂𝐵}\) = 90°
Exercice 3
1. Construis un triangle ABC isocèle en A tel que \( \widehat{𝐵𝐴𝐶}\) = 50°.
2. Marque deux points E et F puis construis leurs images respectives E', F' par la rotation de centre A qui transforme B en C.
Exercice 4
ABCD est un losange de centre J tel que \(\widehat{𝐷𝐴𝐵}\) = 30°.
1. Fais une figure
2. Quelle est l'image de D par la rotation de centre A de sens celui des aiguilles d'une montre et d'angle 30° ?
Exercice 5
1. Trace le segment [AO] de longueur 3 cm.
2. Construis le point M image de A dans la rotation de centre O et d'angle 90°.(sens direct).
3. Construis le point I, image de M dans la rotation dans le sens direct de centre O et d'angle \(\widehat{AOM}\)
4. Construis le point E image de I dans la même rotation.
5. Dans la rotation de centre O et d'angle 90° dans le sens contraire des aiguilles d'une montre, quelle est l'image du point I.
6. Donne la nature du quadrilatère AMIE
Exercice 6
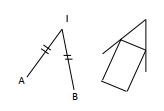
I, A, B sont des points du plan.
Construis la figure ci-contre par la rotation de centre I qui transforme A en B.
Exercice 7
[Ox), [Oy) et [Oz) sont trois demi-droites. A un point situé sur [Ox), B et D sur [Oy) et C sur [Oz),
avec OC = OD = 5 cm et OA = OB = 4 cm ; \(\widehat{xOz}\) = \(\widehat{zOy}\) = 40°.
1. Fais une figure.
2. Démontre que AD = BC en utilisant une rotation à préciser.
Exercice 8
Soit ABCD est un carré de centre I, M et N les milieux respectifs de [AB] et [AD].
1. Fais une figure.
2. Justifie que M est l'image de N dans la rotation de centre I qui transforme A en B.
3. Justifie que ONM est un triangle isocèle.
4. Compare en justifiant:
a. CN et DM.
b. \(\widehat{AIN}\) et \(\widehat{BIM}\)
c. Les aires des triangles BDM et CAN.
d. Les aires des triangles AIN et BIM.
5. Détermine l'aire du quadrilatère AMIN.
Exercice 9
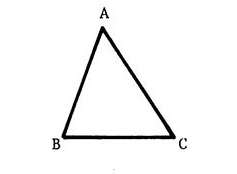
Reproduis le triangle ABC ci-contre.
1. Construis extérieurement à ce triangle
2. les carrés ABDE et ACFG .
3. Démontre que EC = BG et que (EC) est perpendiculaire à (BG).
4. Démontrer que les droites (EC) et (DB) sont perpendiculaires.
5. Comparer les distances EC et DB.
Exercice 10
Le quadrilatère A'B'C'D' est l'image de ABCD par la rotation de centre O et d'angle 60°.
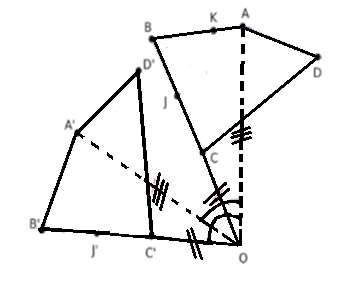
1. Compare en justifiant les aires et les périmètres de ces deux quadrilatères
2. Le point J est le milieu du segment [BC] , son image J' par cette rotation est –elle le milieu du segment [B'C'] ?.Justifie ta réponse.
3. L'angle \(\widehat{𝐴𝐵′𝐶′}\) étant l'image de l'angle \(\widehat{𝐴𝐵𝐶}\) par cette rotation, compare leurs mesures. Justifie ta réponse.
Exercice 11
Construis un triangle AOB isocèle en O tel que AOB ̂ = 45°. Dans la rotation de centre O et d'angle \(\widehat{AOB}\) dans le sens contraire des aiguilles d'une montre, construis :
1. Le point C image de B,
2. Le point D image de C,
3. Le point E image de D,
4. Le point F image de E.
5. Quelle est l'image du point F.
6. Précise la nature du polygone ABCDEF.
Exercice 12
1. Construis un carré CABE de centre I.
2. Par la rotation de centre I et d'angle 45° dans le sens direct, construis M, N, R et S images respectives des points C, A, B, et E.
3. Trace le polygone CMANBRES puis donne sa nature ?
4. Indique le centre et le rayon du cercle circonscrit au polygone CMANBRES.
5. Trace ce cercle circonscrit à ce polygone.
Exercice 13
ABC est un triangle équilatéral de côté 3cm. Le cercle (C ) circonscrit au triangle a pour centre I. Par la rotation de centre I et d'angle 60° dans le sens contraire des aiguilles d'une montre, A a pour image D, B a pour image E et C a pour image F.
1. Construis le triangle ABC puis trace le cercle (C ) .
2. Justifie que les points D, E et F appartiennent au cercle.
3. Donne la nature du polygone ADBECF.
4. Indique le centre et le rayon du cercle inscrit au polygone ADBECF
Exercice 14
1. Construis un triangle IEF isocèle en I dont les angles à la base mesurent 75°.
2. Dans la rotation de sens indirect de centre I qui transforme E en F, construis le point G image de F, le point H image de G, le point R image de H.
3. Quelle est l'image de R ? Précise la nature du polygone EFGHR.
4. Explique comment obtenir le cercle inscrit à ce polygone.