RADIOACTIVITE⚓
II/ LOI DE CONSERVATION DE SODDY⚓
LOI DE CONSERVATION DE SODDY
Une réaction nucléaire est caractérisée par équation symbolisée par des réactifs qui disparaissent, à gauche, et des produits qui apparaissent, à droite, séparés par une flèche indiquant le sens de la transformation.
Au cours d'une réaction nucléaire il y a des grandeurs qui se conservent :
le nombre de masse se conserve : la somme des nombres de masse des réactifs est égale à la sommes des nombres de masse des produits ;
le nombre de charge se conserve : la somme des nombres de charge des réactifs est égale à la sommes des nombres de charge des produits ;
la quantité de mouvement se conserve : la somme des quantités de mouvement des réactifs est égale à la sommes des quantités de mouvement des produits.
1. RADIOACTIVITÉ ALPHA⚓
RADIOACTIVITÉ ALPHA
Au cours d'une radioactivité alpha, il y a une émission d'un noyau d'hélium par un noyau père. la réaction de cette transformation est :
\(_Z^AX\) \(\longrightarrow\) _\(_{Z-2}^{A-4}X \) + \(_2^4He\)
au cours d'une radioactivité alpha le noyau fils a deux protons de moins et quatre nucléons de moins que le noyau père
exemple
le polonium 210 alpha émetteur \(\alpha\). Écrivons l'équation bilan de la désintégration.
\(_{84}^{210}Po\) \(\longrightarrow\) _\(_{82}^{206}Pb \) + \(_2^4He\)
2. RADIOACTIVITÉ beta moins⚓
RADIOACTIVITÉ beta moins
Au cours d'une radioactivité \(\beta^-\), il y a une émission d'un électron \(_{-1}^0e^-\) par un noyau père. La réaction de cette transformation est :
\(_Z^AX\) \(\longrightarrow\) _\(_{Z+1}^{A}X \) + \(_{-1}^0e^-\)
Au cours d'une radioactivité \beta^- le noyau fils a un protons de plus et le meme nombre de nucléons que le noyau père.
exemple
le cobalt 53 est \(\beta^-\). Écrivons l'équation bilan de la désintégration.
\(_{27}^{53}Co\) \(\longrightarrow\) _\(_{28}^{53}Pb \) + \(_{-1}^0e^-\)
3. RADIOACTIVITÉ bêta plus⚓
RADIOACTIVITÉ bêta plus
Au cours d'une radioactivité \(\beta^+\), il y a une émission d'un positon \(_{-1}^0e^+\) par un noyau père. La réaction de cette transformation est :
\(_Z^AX\) \(\longrightarrow\) _\(_{Z-1}^{A}X \) + \(_{-1}^0e^+\)
Au cours d'une radioactivité \(\beta^+\) le noyau fils a un proton de moins et le même nombre de nucléons que le noyau père.
exemple
le phosphore 30 est \(\beta^+\). Écrivons l'équation bilan de la désintégration.
\(_{15}^{30}P\) \(\longrightarrow\) _\(_{14}^{30}Si \) + \(_{-1}^0e^+\)
Equation différentielle d'ordre 1 : Loi de décroissance radioactive⚓
Exemple : Loi de décroissance radioactive
Décroissance exponentielle du nombre de noyaux radioactifs :
Soit \(n(t)\), le nombre de noyaux présents dans un échantillon d'isotopes radioactifs à une date \(t\).
La vitesse de désintégrations nucléaires spontanées dans le temps est proportionnelle au nombre de noyaux \(n(t)\).
Cela se représente par l'équation différentielle suivante :
\(\dfrac{{\rm d}n(t)}{{\rm d}t}=-\lambda\, n(t)\).
Le membre de gauche représente une dérivée par rapport au temps de la fonction \(n\) ; on peut la noter \(n'\) ce qui nous ramène à l'équation \(n'=-\lambda\, n\) (qui est une équation du type \(y'=a\, y\)).
Pour résoudre une telle équation on peut procéder comme suit :
\(y'=a\,y\) ce qui se réécrit \(\dfrac{y'}y=a\). En intégrant de part et d'autre on a \(\displaystyle\int_{t_0}^t\dfrac{y'}y\,{\rm d}s=\displaystyle\int_{t_0}^ta\,{\rm d}s\). Pour simplifier l'écriture nous nous plaçons dans le cas \(y>0\) pour ne pas avoir à écrire tout le temps \(|y|\) (justifié ici par le fait que \(n>0\)).
On obtient donc \(\ln (y)-\ln(y(t_0)) = a(t-t_0)\), soit \(\ln(y)=a\cdot t +\ln(y(t_0))-a\cdot t_0\).
En passant à l'exponentielle (afin de déterminer \(y\)), on obtient \(y=y_0\cdot {\rm e}^{a\cdot t}\) où \(y_0={\rm e}^{\ln(y(t_0))-a\cdot t_0}\).
La solution de cette équation différentielle est la loi de décroissance radioactive. D'après ci-dessus, en substituant \(y\) par \(n\), on a
\({\color{white}.}\qquad\qquad\qquad n(t)=n_0\cdot{\rm e}^{-\lambda t}\).
\(n_0\) est le nombre de noyaux présents dans l'échantillon d'isotopes radioactifs à l'instant \(t=0\) (instant initial).
Temps de désintégration radioactive :
C'est la durée \(t\) nécessaire pour qu'il reste une quantité \(N\) de noyaux radioactifs. Il est obtenu comme suit :
\(N(t)=N=n_0\cdot{\rm e}^{-\lambda t}\) il vient \({\rm e}^{-\lambda t}=\dfrac N{n_0}\). Par suite on a
\(t=-\dfrac 1\lambda \ln(N/n_0)\).
Cas particulier : Le temps de demi-vie radioactive :
D'après ci-dessus, le temps de demi-vie radioactive est donnée par
\(t=\dfrac 1\lambda \ln(2)\).
4. RADIOACTIVITÉ GAMMA⚓
RADIOACTIVITÉ GAMMA
La radioactivité gamma \(_0^0\gamma\) correspond à une émission de photons ; c'est-à-dire de la lumière. La radioactivité \(\gamma\) accompagne les autres radioactivité. le noyau fils issu de la désintégration est dans un état excité. En se existant, le noyau fils émet un photon \(\gamma\).
l'équation de la desintégration \(\gamma\) est
\(_Z^AX^*\)\(l\longrightarrow \) \(_Z^AX\) + \(\gamma\)
III/ ÉTUDE ÉNERGÉTIQUE DE LA RADIOACTIVITÉ⚓
ÉTUDE ÉNERGÉTIQUE DE LA RADIOACTIVITÉ
Les transformations nucléaires sont très énergétiques.
1. Énergie de liaison par nucléon⚓
1.1 DÉFAUT DE MASSE⚓
Le défaut de masse \(\delta\)m représente la différence entre la masse des nucléons pris isolément et la masse du noyau. Le défaut de msse s'exprime en unité de masse atomique u. 1u = 931,5 Mev/C²=1,66.10^{-27} kg.
\(\delta\)m = Z mp + N mn - mnoyau
1.2 ÉNERGIE DE LIAISON⚓
L'énergie de liaison El représente l'énergie qui lie les nucléons entre eux.
El=\(\delta\)m . c²
1.3 ÉNERGIE DE LIAISON PAR NUCLÉON EA⚓
L'énergie de liaison par nucléon EA représente le rapport entre l'énergie de liaison et le nombre de masse \(E_A=\frac{El}{A}\). Elle s'exprime en Mev/nucléon. Cette grandeur est un indicateur de la stabilité d'un noyau. Plus l'énergie de liaison par nucléon est grande, plus le noyau est stable.
2. ÉNERGIE LIBÉRÉE PAR UNE RÉACTION⚓
2. ÉNERGIE LIBÉRÉE PAR UNE RÉACTION
D’après le principe d'équivalence masse-énergie, la perte de masse est équivalente à l'énergie l'énergie libérée par la réaction nucléaire.
Elib=\(Δm\)*c² où \(Δm\) représente la perte de masse et c la célérité de la lumière.
IV/ LOI DE DÉCROISSANCE RADIOACTIVE⚓
1. Énoncé⚓
Quantification de la radioactivité
1. Énoncé
le nombre de particules radioactives diminue toujours au cours du temps. la vitesse de disparition des particules est proportionnelle au nombre de particules radioactives :
\(-\frac {dN}{dt}=λN\)
la solution de cette équation différentielle est :
\(N=N_0e^-{λt} \) où
\(N_0\) représente le nombre de particules initial
N est le nombre de particules restant
\(λ\) est la constante radioactive
cette relation est aussi vérifiée par la masse de la substance radioactive
\(m(t)=m_0e^-{λt}\)
m est la masse restante
m0 est la masse restante
cette relation permet de déterminer l'age t de l'échantillon
\(\frac{ln\frac{N}{N_0}}{λ}\)
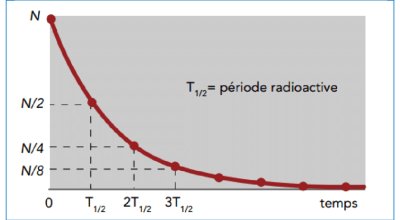
2. PÉRIODE RADIOACTIVE⚓
V/ACTIVITÉ A⚓
ACTIVITÉ A
l’activité radioactive est le nombre de désintégration par seconde. Elle s'exprime en becquerel (Bq) ; \(A=-\frac{dN}{dt}\).
Ainsi on obtient A=λ N.
l'activité est proportionnelle au nombre de particules radioactives. or N=n \(N_a\)
n est l nombre de mol
\(N_a\) est le nombre d'Avogadro \(N_a\)=6,02.\(10^{23}\)
VI/ APPLICATIONS DE LA RADIOACTIVITÉ⚓
APPLICATIONS DE LA RADIOACTIVITÉ
Utilisation des rayonnements peut être positive et négative
applications utiles
- Médecine : imagerie, radio, scanner, scintigraphie, radiothérapie, stérilisation des matériels et des instruments, exemple : Détection de tumeurs cancéreuses, Étude du fonctionnement du cerveau.
-Science : La datation, exemple : l'âge des roches (La demi-vie (T1/2) )
-Alimentation : stérilisation et conservation -Agriculture : traceurs
-Environnement : marquage
-Énergie : production d'électricité
applications négatives
-Essais nucléaires et bombes
-Déchets
-Accidents
Exercices sur la radioactivité⚓
Applications⚓
Application 1 : Stabilité des noyaux
Question⚓
L'énergie de liaison du nucléide\(\ _{92}^{238}U\) est \(E_{L1}=1802 MeV\); celle du nucléide \(\ _{58}^{142}Ce\) est \(E_{L2}=1199,9 MeV\).
Lequel de ces deux nucléides est plus stables ? Justifier.
Solution⚓
Pour comparer la stabilité des noyaux on utilise l'énergie de liaison par nucléon. Un nucléide est d'autant plus stable que son énergie de liaison par nucléon est élevée.
\(\frac{E_{L1}}{A_1}=\frac{1802}{238}=7,57 MeV/nucléon\)
\(\frac{E_{L2}}{A_2}=\frac{1199,9}{142}=8,45 MeV/nucléon\)
\(\frac{E_{L1}}{A_1}<\frac{E_{L2}}{A_2}\): le césium 142 (\(\ _{58}^{142}Ce)\) est plus stable que l'uranium 238.
Application 2 : Réaction nucléaire - Énergie libérée
Question⚓
On donne la réaction \(^{210}_{84}Po\rightarrow\ ^4He +\ _{82}Pb\).
1. Compléter l'équation nucléaire.
2. Calculer en MeV puis en joule l'énergie libérée au cours de cette réaction.
On donne les masses de certains noyaux : \(m_1 = m(Po)= 210,0857 u\); \(m_2=m(He)=4,00387 u\); \(m_3=m(Pb)=206,03854 u\); \(1 u=931,5 MeV/c^2\)
Solution⚓
1.Équation nucléaire
Pour compléter l'équation nous appliquons les lois de conservation du nombre de masse et du nombre de charge.
\(210 =4+x \Longrightarrow x = 206\); \(84=y+82 \Longrightarrow y=2\)
\(\ ^{210}_{84}Po \rightarrow \ ^4_2He + \ ^{206}_{82}Pb\)
2. Énergie libérée au cours de cette réaction nucléaire
\(E=\Delta m c^2 = (m_1 -(m_2 +m_3))c^2\)
En MeV : \(E = (210,0857 - (4,00387 + 206,03854)\times 931,5 =40,3 MeV\)
En joule : \(E =40,3\times 1,6.10^{-13}= 6,45.10^{-12} j\)
Application 3 : Nombre de noyaux désintégrés et activité d'une source radioactive
Question⚓
L'azote \(\ ^{13}_7N\) est radioactif émetteur \(\beta^+\). Il se désintègre pour donner le carbone
\(\ ^{A}_{Z}C\). Sa période ou demi-vie vaut T = 10 min.
1. Écrire l'équation de la désintégration.
2. Un échantillon d'azote contenait initialement 16000 noyaux.
2.1 calculer le nombre de noyaux désintégrés à la date t = 30 min.
2.2 Calculer l'activité de la source radioactive à cette date.
Solution⚓
1. Équation de la désintégration
\(\ ^{13}_7N \rightarrow \ ^0_{+1}e + \ ^{A}_{Z}C\)
Les lois de conservation du nombre de masse et du nombre de charge \(\Longrightarrow\) A = 13 et Z = 6
soit donc \(\color{blue}\ ^{13}_7N \rightarrow \ ^0_{+1}e + \ ^{13}_{6}C\)
2.1 Nombre noyaux désintégrés
soient : \(N_0\) le nombre initial de noyaux d'azote, N le nombre de noyaux d'azote restants et x le nombre de noyaux d'azote désintégrés.
Loi de décroissance radioactive : \(N=N_0e^{\lambda t}=\frac{N_0}{2^n}\)
Ici, t = 3T \(\Longrightarrow\) n = 3 et \(N = \frac{N_0}{2^3} = \frac{16000}{8} =2000 noyaux\)
Loi de conservation de la quantité de matière : \(x = N_0 - N = 16000-2000 = 14000 noyaux\)
2.2 Activité de la source radioactive
Par définition \(A = \lambda N = \frac{ln2}{T}\times N = \frac{ln2}{600}\times 2000 = 2,31 Bq\)
Application 4 : Âge de la lune.
Question⚓
L'isotope potassium \(\ ^{40}_{19}K\) pour donner de l'argon \(\ ^{40}_{18}Ar\). La période du potassium est \(T=1,5.10^9\)ans.
1. Écrire l'équation de désintégration.
2. Calculer la constante radioactive \(\lambda\).
3. Pour déterminer l'âge de la lune, on procède à l'analyse de cailloux rapportés de cet astre.
L'analyse d'un échantillon montre que celui-ci renferme \(8,2.10^{-4} cm^3\) d'argon 40 (emprisonné dans le caillou) et \(1,66.10^{-6}\) g de potassium 40.
Trouver l'âge des cailloux.
On suppose que lors de sa formation le caillou ne renfermait que du potassium. Les volumes sont mesurés dans les C.N.T.P.
Solution⚓
1. Équation de désintégration
\(\ ^{40}_{19}K \rightarrow \ ^{40}_{18}Ar + \ ^a_zX\)
Lois de conservation : \(40=40+a \rightarrow a=0\) et \(19=18+z \rightarrow z=1\) soit donc \(X=\ ^0_{+1}e\)
\(\color{blue}\ ^{40}_{19}K \rightarrow \ ^{40}_{18}Ar + \ ^0_{+1}e\)
2. Constante radioactive \(\lambda\)
\(\color{blue}\lambda=\frac{ln2}{T}=\frac{ln2}{1,5.10^9}=462.10^{-12} an^{-1}\)
3. Âge de la lune.
soient
\(n=\frac{m_K}{M_K}=\frac{1,66.10^{-6}}{40}=4,15.10^{-8} mol\) le nombre de mol de potassium présent.
\(x=\frac{V}{V_M}=\frac{8,2.10^{-7}}{22,4}=3,661.10^{-8} mol\) le nombre de mol d'argon présent mais aussi le nombre de mol de potassium désintégré.
\(n_0=n+x=4,15.10^{-8} +3,661.10^{-8}=7,811.10^{-8} mol\) le nombre mol initial de potassium.
Loi de décroissance radioactive : \(n=n_0e^{-\lambda t}\) \(\Longrightarrow\)\(-\lambda t=ln\frac{n}{n_0}\) soit donc \(\color{blue}{t=-\frac{1}{\lambda}\times ln\frac{n}{n_0}=-\frac{1}{462.10^{-12}}\times ln\frac{4,15.10^{-8}}{7,811.10^{-8}}=1,37.10^9 ans}\)