Définition : Maximum, minimum d'une fonction
On dit qu'une fonction \(f\) définie en \( a\) admet un maximum (respectivement un minimum) en ce point, s'il existe un intervalle \(I\) contenant \(a\) tel que : \(\forall x\in I \quad f(x)\leq f(a)\) (respectivement \(f(x)\geq f(a)\)). \(f(a)\) est le maximum (respectivement le minimum) de la fonction sur \( I\).
\(f\) admet un extremum sur un intervalle, s'il admet un maximum ou un minimum sur cet intervalle.
Exemple :
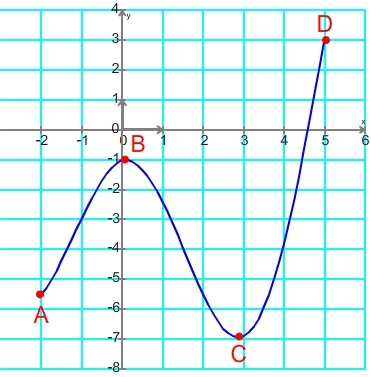
La fonction présente un minimum en -2 (abscisse de A), un minimum en 3 (abscisse de C), un maximum en 0 ( abscisse de B), un maximum en 5 ( abscisse de D).
Méthode : Extremum d'une fonction dérivable
Soit \(f\) une fonction dérivable sur un intervalle \(I\) contenant un point \(a\). \(f\) admet un extrémum au point \(a\), si et seulement si sa dérivée \(f'\) s’annule au point \( a\) en changeant de signe.
Exemple :
Point d'inflexion⚓
Définition :
Soit \(f\) une fonction définie sur un intervalle \(I\) contenant un point \(a\). On dit que admet \(f\) admet un point d'inflexion en \(a\), si sa courbe représentative change de concavité au point d'abscisse \( a\).
Exemple :
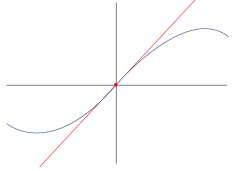
La courbe change de concavité à l'origine
Exemple : Reconnaître un point d'inflexion
Méthode : Recherche de point d'inflexion
Soit \(f\) une fonction deux fois dérivable sur un intervalle \(I\) contenant un point \(a\). \(f\) admet un point d'inflexion en \(a\), si et seulement si sa dérivée seconde \(f''\) s’annule au point \( a\) en changeant de signe.