Testez-vous en mathématiques pour préparer votre première année à l'université !
Questions de connaissance
?Question
Énoncé
On considère une série statistique à 13 éléments décrite par la courbe de ses fréquences cumulées croissantes :
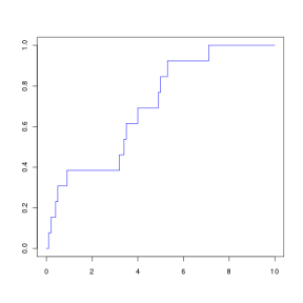
Lequel des dessins suivants peut correspondre à son diagramme en boîte ?
Correction
Explication Générale
Notons \(\textstyle{x_1\leq x_2\leq\cdots\leq x_{13}}\) les 13 éléments de la série rangés par ordre croissant. Le minimum de la série est \(\textstyle{x_1}\) , le premier quartile est \(\textstyle{x_4}\) , la médiane est \(\textstyle{x_7}\) , le troisième quartile est \(\textstyle{x_{10}}\) et le maximum est \(\textstyle{x_{13}}\)
D'après le graphe des fréquences cumulées, \(\textstyle{x_1}\) est proche de \(\textstyle{0}\) , \(\textstyle{x_4}\) est inférieur à 1, \(\textstyle{x_7}\) est entre 3 et 4, \(\textstyle{x_{10}}\) est proche de 5 et \(\textstyle{x_{13}}\)
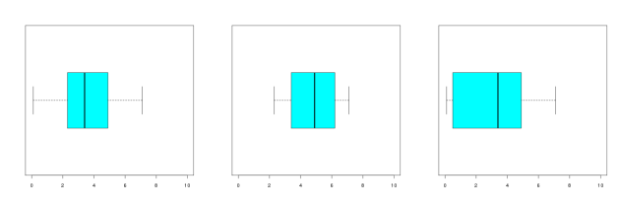
Le minimum de la série associée au dessin du milieu est supérieur à 2 ; ce ne peut donc être la bonne réponse.
Le premier quartile de la série associée au dessin de gauche est supérieur à 2 ; ce ne peut donc être la bonne réponse.
Le dessin de droite correspond à la série initiale.
?Question
Énoncé
On considère une série statistique à 13 éléments décrite par sa courbe des fréquences cumulées croissantes :
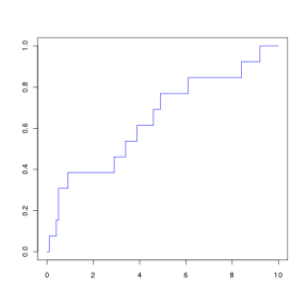
Lequel des dessins suivants peut correspondre à son diagramme en boîte ?
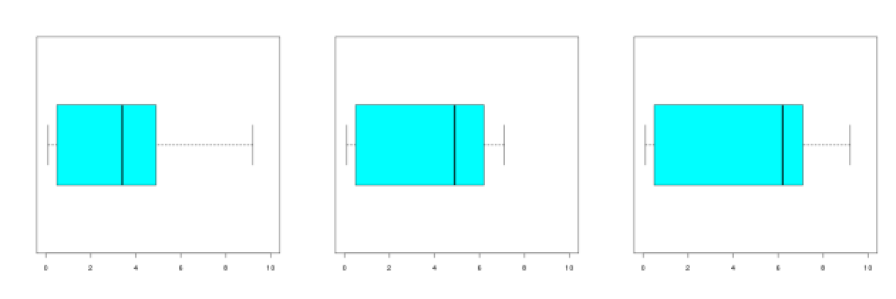
Correction
Explication Générale
Notons \(\textstyle{x_1\leq x_2\leq\cdots\leq x_{13}}\) les 13 éléments de la série rangés par ordre croissant. Le minimum de la série est \(\textstyle{x_1}\) , le premier quartile est \(\textstyle{x_4}\) , la médiane est \(\textstyle{x_7}\) , le troisième quartile est \(\textstyle{x_{10}}\) et le maximum est \(\textstyle{x_{13}}\)
D'après le graphe des fréquences cumulées, \(\textstyle{x_1}\) est proche de \(\textstyle{0}\) , \(\textstyle{x_4}\) est inférieur à 1, \(\textstyle{x_7}\) est entre 3 et 4, \(\textstyle{x_{10}}\) est proche de 5 et \(\textstyle{x_{13}}\)
Le maximum de la série associée au dessin du milieu est proche de 7 ; ce ne peut donc être la bonne réponse.
La médiane de la série associée au dessin de droite est proche de 6 ; ce ne peut donc être la bonne réponse.
Le dessin de gauche correspond à la série initiale.
?Question
Énoncé
On considère une série statistique à 13 éléments décrite par sa courbe des fréquences cumulées croissantes :
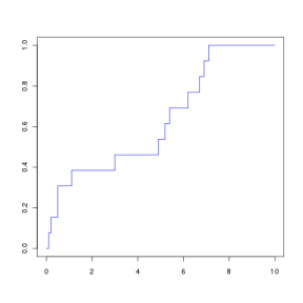
Lequel des dessins suivants peut correspondre à son histogramme (en fréquence) ?
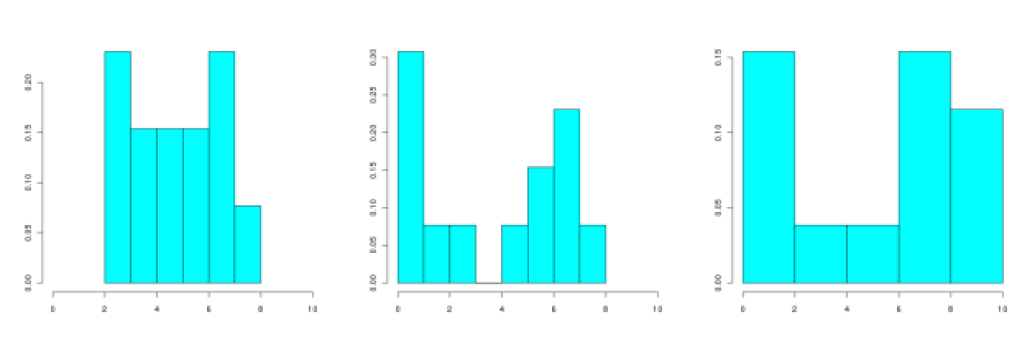
Correction
Explication Générale
D'après le graphe des fréquences cumulées, le minimum est proche de \(\textstyle{0}\)
Le minimum de la série associée au dessin de gauche est supérieur à 2 ; ce ne peut donc être la bonne réponse.
Le maximum de la série associée au dessin de droite est supérieur à 8 ; ce ne peut donc être la bonne réponse.
Le dessin du milieu correspond à la série initiale.
?Question
Énoncé
On considère une série statistique à 13 éléments décrite par sa courbe des fréquences cumulées croissantes :
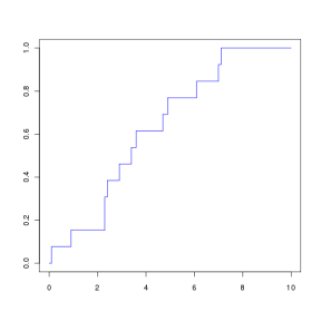
Lequel des graphiques suivant peut correspondre à son histogramme (en fréquence) ?
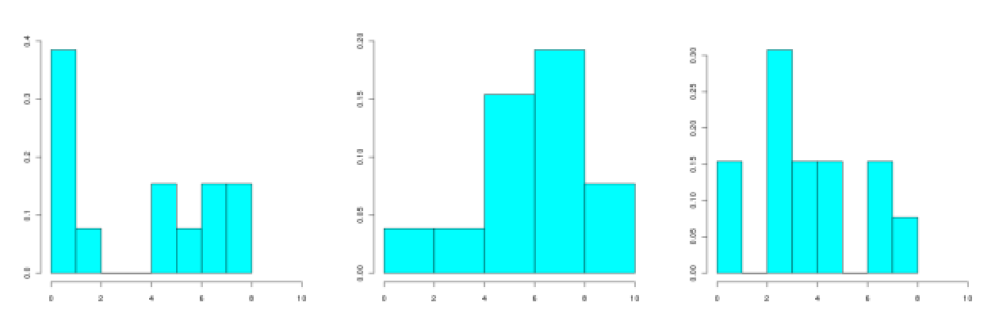
Correction
Explication Générale
D'après le graphe des fréquences cumulées, le minimum de la série est proche de \(\textstyle{0}\)
Le maximum de la série associée au dessin du milieu est supérieur à 8 ; ce ne peut donc être la bonne réponse.
Il n'y a aucun élément entre 2 et 4 dans la série associée au diagramme de gauche ; ce ne peut donc être la bonne réponse.
Le dessin de droite correspond à la série initiale.
?Question
Énoncé
On considère une série statistique à 13 éléments décrite par son histogramme (en fréquence) :
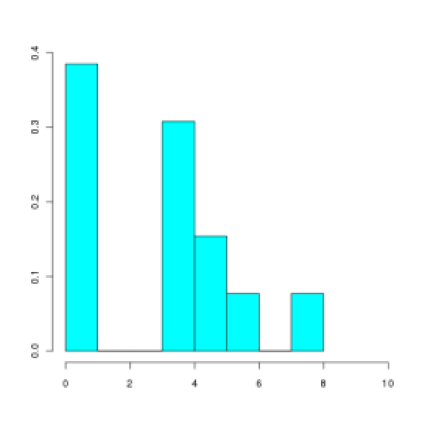
Lequel des graphiques suivant peut correspondre à sa courbe des fréquences cumulées croissantes ?
Correction
Explication Générale
D'après l'histogramme, le minimum de la série est entre 0 et 1, le maximum entre 7 et 8, et il n'y a pas d'élément entre 1 et 3, ni entre 6 et 7.
Le minimum de la série associée au dessin du milieu est supérieur à 2 ; ce ne peut donc être la bonne réponse.
La maximum de la série associée au dessin de gauche est proche de 9 ; ce ne peut donc être la bonne réponse.
Le dessin de droite correspond à la série initiale.
?Question
Énoncé
On considère une série statistique à 13 éléments décrite par son histogramme (en fréquence) :
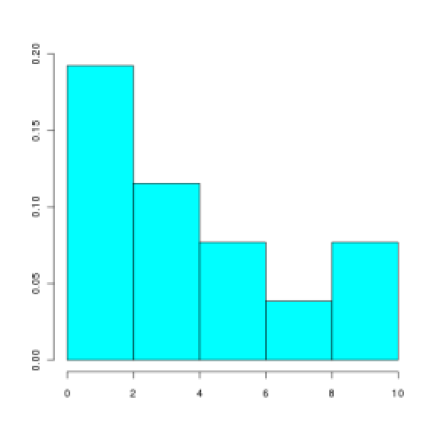
Lequel des graphiques suivant peut correspondre à sa courbe des fréquences cumulées croissantes ?
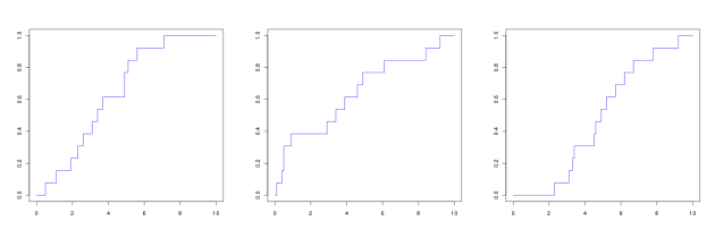
Correction
Explication Générale
D'après l'histogramme, le minimum de la série est entre 0 et 2 et le maximum entre 8 et 10.
Le maximum de la série associée au dessin du gauche est inférieur à 8 ; ce ne peut donc être la bonne réponse.
Le minimum de la série associée au dessin de droite est supérieur à 2 ; ce ne peut donc être la bonne réponse.
Le dessin du milieu correspond à la série initiale.
?Question
Énoncé
On considère la série statistique à 13 éléments suivante :
\(\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline6.2&4.9&6.6&7.1&6.2&9.2&3.0&5.7&9.1&0.1&7.3&4.9&4.7\\\hline\end{array}\)
Lequel des graphiques suivant peut correspondre à son histogramme (en fréquence) ?
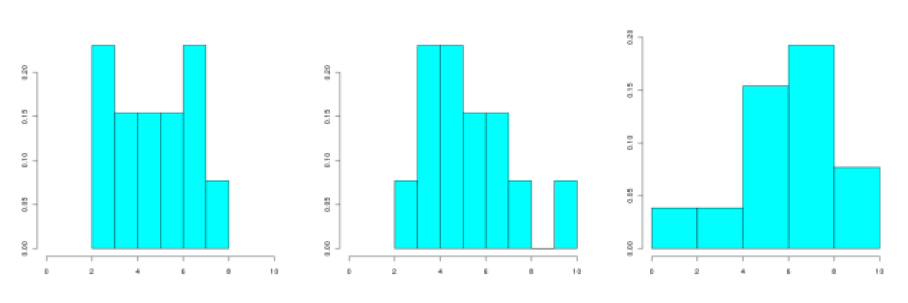
Correction
Explication Générale
Au vu des données, le minimum de la série est égal à \(\textstyle{0.1}\)
Le minimum de la série associée au dessin du gauche est supérieur à 2 ; ce ne peut donc être la bonne réponse.
Il en est de même pour la série associée au dessin du milieu.
Le dessin de droite correspond à la série initiale.
?Question
Énoncé
Trois élèves \(\textstyle{x, y}\) et \(\textstyle{z}\) attendent dans la file d'attente de la cantine. On considère les événements \(\textstyle{A=}\) « \(\textstyle{y}\) attend derrière \(\textstyle{x}\) » et \(\textstyle{B=}\) « \(\textstyle{z}\) attend derrière \(\textstyle{x}\) » . On suppose qu'il y a équiprobabilité sur l'ordre des arrivées des élèves dans la file d'attente. Les événements \(\textstyle{A}\) et \(\textstyle{B}\) sont-ils indépendants ?
Correction
Explication Générale
Il y a \(\textstyle{3 !=6}\) ordres possibles dans la file d'attente. L'événement \(\textstyle{A\cap B}\) est égal à \(\textstyle{\{z\leq y\leq x, y\leq z\leq x\}}\) de probabilité \(\textstyle{\frac{2}{6}= \frac{1}{3}}\) . L'événement \(\textstyle{A}\) est égal à \(\textstyle{\{y\leq x\leq z, y\leq z\leq x, z\leq y\leq x\}}\) de probabilité \(\textstyle{\frac{3}{6}=\frac{1}{2}}\) . De même, \(\textstyle{\mathbb{P}(B)=\frac{1}{2}}\) . Ainsi \(\textstyle{\mathbb{P}(A\cap B)\neq \mathbb{P}(A)\mathbb{P}(B)}\)
?Question
Énoncé
La densité d'une variable uniforme sur l'intervalle \(\textstyle{[-1, 3]}\) vaut :
Correction
Explication Générale
L'expression de la densité de probabilité pour une variable qui suit une loi uniforme sur un intervalle \([a,b]\) est \(f(x) =\frac {1}{(b-a)}\) si \(x\) appartient à \([a,b]\)
?Question
Énoncé
Soit \(\textstyle{X}\) une variable normale centrée réduite. Alors la variance de la variable \(\textstyle{Y=2X+5}\) est strictement plus grande que la variance de la variable \(\textstyle{Z=2X+3}\)
Correction
Explication Générale
\(\textstyle{Y}\) et \(\textstyle{Z}\)
?Question
Énoncé
La fonction exponentielle \(x \mapsto \exp(x)\) vérifie
Correction
Explication Générale
Voici deux ressources pour revoir quelques notions essentielles :
?Question
Énoncé
La fonction \(f:x \mapsto \frac{\ln(x)}{x}\)
Correction
Explication Générale
Voici deux ressources pour revoir quelques notions :
?Question
Énoncé
La fonction dérivée de \(\ln |u(x)|\)
Correction
Explication Générale
Pour commencer, on peut bien sûr considérer le cas où la fonction \(u\) a des valeurs positives, ce qui permet d'éliminer certaines réponses... On passe ensuite, prudemment, au cas où \(u\) prend des valeurs négatives (\(|u|=-u\))
?Question
Énoncé
Le nombre complexe \(e^{i\frac{\pi}{2}}\) est égal à :
Correction
Explication Générale
Si on ne connaît pas d'emblée la réponse, il vaut mieux repasser par la forme trigonométrique : \(e^{i\frac{\pi}{2}}=\cos(\frac{\pi}{2})+i\sin(\frac{\pi}{2})\)
?Question
Énoncé
Le nombre complexe \(e^{2i\pi}\) est égal à :
Correction
Explication Générale
Si on ne connaît pas d'emblée la réponse, il vaut mieux repasser par la forme trigonométrique : \(e^{2i\pi}=\cos(2\pi)+i\sin(2\pi)\)
?Question
Énoncé
Le nombre complexe \(e^{i\pi}\) est égal à :
Correction
Explication Générale
Si on ne connaît pas d'emblée la réponse, il vaut mieux repasser par la forme trigonométrique : \(e^{i\pi}=\cos(\pi)+i\sin(\pi)\)
?Question
Énoncé
Calculer le module du nombre complexe \(x + \imath y\), x et y étant tout deux des réels
Correction
Explication Générale
Il faut connaître la définition du module \(|z|=\sqrt{z\overline{z}}\)
?Question
Énoncé
Pour tout nombre complexe \(z\),
Correction
?Fonction croissante/décroissante (1)
Énoncé
Quels arguments sont valides pour justifier que la fonction \(x \mapsto \sin(x)\) n'est pas une fonction croissante sur \(\mathbb{R} ?\)
Correction
Explication Générale
Une fonction \(f\) est croissante si \(x \le y\) implique \(f(x) \le f(y)\). Donc une fonction n'est pas croissante si on peut trouver \(x \le y\) mais avec \(f(x) > f(y).\) Le seul argument valable est donc \(\frac{3\pi}{4} < \pi\) avec \(\sin(\frac{3\pi}{4}) > \sin(\pi)\).
Pour aller plus loin :
cours : Limites et fonctions continues
vidéo : Continuité en un point
vidéo : Fonctions monotones
vidéo : La bijection
exercices : Fonctions continues
?Fonction croissante/décroissante (3)
Énoncé
Quelles sont les assertions vraies ?
Correction
Explication Générale
La fonction \(x \mapsto \frac{1}{x}\) est décroissante sur \(]0,+\infty[\) et \(]-\infty,0[\) mais pas sur \(\mathbb{R}^*\).
Pour aller plus loin :
cours : Limites et fonctions continues
video : Fonctions monotones
video : Fonctions périodiques
?Fonctions - continuité en un point (1)
Énoncé
Quelles fonctions sont continues en \(x=0\) ?
Correction
Explication Générale
La fonction inverse n'est pas définie à l'origine ! La fonction partie entière n'est pas continue à l'origine.
Pour aller plus loin :
cours : Limites et fonctions continues
video : Continuité en un point
exercices : Fonctions continues
?Fonctions - continuité sur un intervalle (2)
Énoncé
Quelles sont les propriétés vraies ?
Correction
Explication Générale
Le quotient de deux fonctions continues est une fonction continue, uniquement aux points où le dénominateur ne s'annule pas.
Pour aller plus loin :
cours : Limites et fonctions continues
video : Notion sur les fonctions
exercices : Fonctions continues
?Fonction bijective (2)
Énoncé
Soit \(f : [a,b] \to [c,d]\) continue avec \(a < b\), \(c < d\), \(f(a)=c\), \(f(b)=d\). Quelles propriétés impliquent \(f\) bijective ?
Correction
Explication Générale
Comme \(f(a)=c\), \(f(b)=d\), alors par le théorème des valeurs intermédiaires, toute valeur entre \(c\) et \(d\) est atteinte, autrement dit \(f\) est surjective. Si en plus \(f\) est injective (ce qui est le cas si \(f\) strictement croissante) alors \(f\) sera bijective.
Pour aller plus loin :
cours : Limites et fonctions continues
video : La bijection
exercices : Fonctions continues
?Fonctions réelles - dérivée en un point (4)
Énoncé
Soit \(f(x)=\left\{\begin{array}{cl}\displaystyle x+x^2\sin \frac{1}{x}&\mbox{si }x\neq 0\\ \\ 0&\mbox{si }x=0.\end{array}\right.\) Quelles sont les bonnes réponses ?
Correction
Explication Générale
On a \(\lim_{x\to 0}\frac{f(x)-f(0)}{x-0}=\lim_{x\to 0}\left(1+x\sin \frac{1}{x}\right)=1.\) Donc, \(f\) est dérivable en \(0\) et \(f'(0)=1\).
Pour aller plus loin :
cours : Dérivée d'une fonction
video : Définition de la dérivée
video : Calculs
exercices : Fonctions dérivables
?Polynômes -polynôme dérivé
Énoncé
Soit \(P(X) = \sum_{k=0}^n a_k X^k\), les \(a_i\) sont des réels ou des complexes.
On associe le polynôme dérivé : \(P'(X) = \sum_{k=1}^n ka_k X^{k-1}\). Quelles sont les affirmations vraies ?
Correction
Explication Générale
Le polynôme dérivé s'obtient comme si on dérivait la fonction \(X \mapsto P(X)\).
Pour aller plus loin :
cours : Polynômes
?Limites des fonctions réelles - limite en l'infini d'une fraction rationnelle (1)
Énoncé
Soit \(f(x)= \frac{x^2+2x+1}{x^2-x-1}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
La limite en l'infini d'une fraction rationnelle est la limite de la fraction de ses monômes de plus haut degré.
Pour aller plus loin :
exercices : Limites de fonctions
?Limites des fonctions réelles - limite en un point
Énoncé
Soit \(a\in \mathbf{R}\), \(I\) un intervalle contenant \(a\) et \(f\) une fonction définie sur \(I \setminus\{a\}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Voir la définition d'une limite finie ou infinie en un point \(a\in\mathbf{R}\) : \(\lim_{x\to a} f(x)=l\) si et seulement si \(\forall \epsilon > 0, \exists \alpha > 0, \forall x \in I\setminus\{a\}, |x-a| < \alpha \Rightarrow |f(x)-l| < \epsilon\) \(\lim_{x\to a} f(x)=-\infty\) si et seulement si \(\forall A < 0, \exists \alpha > 0, \forall x \in I\setminus\{a\}, |x-a| < \alpha \Rightarrow f(x) < A\)
Pour aller plus loin :
?Limites des fonctions réelles - limite en l'infini
Énoncé
Soit \(f\) une fonction définie sur \(\mathbf{R}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Voir la définition d'une limite en \(+\infty\) ou \(-\infty\) vers une valeur finie ou infinie : \(\lim_{x\to +\infty} f(x)=l \, (l\in \mathbf{R})\) si et seulement si \(\forall \epsilon > 0, \exists A > 0, \forall x \in \mathbf{R}, x\ge A \Rightarrow |f(x)-l|\le \epsilon\) \(\lim_{x\to -\infty} f(x)=+\infty\) si et seulement si \( \forall A > 0, \exists B < 0, \forall x \in \mathbf{R}, x\le B \Rightarrow f(x)\ge A\)
Pour aller plus loin :
?Limites des fonctions réelles - fonction sinus
Énoncé
Soit \(f(x)= \sin x\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Toute fonction périodique non constante n'admet pas de limite en l'infini.
Pour aller plus loin :
video : La fonction sinus
?Nombres complexes - module/argument
Énoncé
Soit \(\theta \in \mathbf{R}\). \(e^{i\theta}\in \mathbf{R}\) si et seulement si :
Correction
Explication Générale
\(e^{i\theta}= \cos \theta + i \sin \theta \) et \(\sin \theta = 0 \) si et seulement si \(\theta =k\pi\), \(k \in \mathbf{Z}\).
Pour aller plus loin :
video : Module d'un nombre complexe
video : Notation exponentielle
video : Argument d'un nombre complexe
?Nombres complexes - trigonométrie
Énoncé
Soit \(\theta\) un réel. Quelles sont les assertions vraies ?
Correction
Explication Générale
On peut appliquer les formules d'Euler ou de Moivre, ou utiliser la formule d'addition du cosinus.
Pour aller plus loin :
?Nombres complexes - trigonométrie
Énoncé
Soit \(\theta\) un réel. Quelles sont les assertions vraies ?
Correction
Explication Générale
On peut appliquer la formule de Moivre, ou utiliser les formules d'addition du cosinus et du sinus et procéder par identification.
Pour aller plus loin :
?Divisibilité
Énoncé
L'énoncé suivant est-il correct ?
Soient \(a,b\) et \(c\) des entiers, avec \(b\) et \(c\) premiers entre eux. On suppose que \(a\) divise le produit \(bc\).
Alors \(a\) divise \(b\) ou \(a\) divise \(c\).
Correction
Explication Générale
Par exemple, si l'on prend \(a=6,\) \(b=2\) et \(c=3\). Les nombres entiers \(2\) et \(3\) sont premiers entre eux, \(6\) divise \(3\times 2\), néanmoins \(6\) ne divise pas \(2\) ni \(3\).
?Divisibilité
Énoncé
L'énoncé suivant est-il correct ?
Soient \(a,b\) des entiers, et \(p\) un nombre premier. On suppose que \(p\) divise le produit \(ab\).
Alors \(p\) divise \(a\) ou \(p\) divise \(b\).
Correction
Explication Générale
C'est l'énoncé du lemme de Gauss.
Pour aller plus loin : http://uel.unisciel.fr/mathematiques/arithmetique/arithmetique_ch03/co/apprendre_ch3_04.html
?Congruences
Énoncé
A quel entier est congru \(25\) modulo \(4\) ?
Correction
Explication Générale
On a : \(25 = 6 \times 4 +1\), donc : \(25 \equiv 1 \; [4]\).
?Fonctions usuelles
Énoncé
La fonction exponentielle vérifie l'équation fonctionnelle :
Correction
Explication Générale
Pour un rappel sur les propriétés usuelles de la fonction exponentielle, voir :
http://ressources.unisciel.fr/ramses/517-18-exponentielles_log/co/fa501_2_4.html
?Limite d'une suite
Énoncé
La suite \((u_n)_{n \in \mathbb N}\) converge vers le nombre réel \(\ell\) si :
Correction
Explication Générale
C'est la définition d'une suite convergente vers la limite \(\ell\).
Pour aller plus loin : http://ressources.unisciel.fr/ramses/517-521-suites/co/fa101_4.html
?Suites bornées
Énoncé
Soit \((u_n)\) une suite de nombres réels positifs. L'affirmation suivante est-elle vraie :
``Si \((u_n)\) n'est pas bornée, alors \(u_n\xrightarrow[n \to +\infty]{} +\infty\). "
Correction
Explication Générale
Par exemple, la suite de terme général :
\(u_n=\begin{cases}0 & \text { si $n$ est pair} \cr n & \text{ si $n$ est impair}\end{cases}\)
n'est pas bornée, mais ne tend pas vers \(+\infty\).
?Suites adjacentes
Énoncé
Soient \((u_n), (v_n)\) deux suites de réels telles que l'on ait :
\(\forall n \in \mathbf N,\, u_n \leq v_n \quad \text{ et } \quad v_n-u_n \xrightarrow[n \to +\infty]{}0\).
Que peut-on en déduire?
Correction
Explication Générale
Par exemple, pour les suites \(u_n=v_n=n\), aucune des affirmations n'est vraies. Dans le théorème des suites adjacentes, il y a des hypothèses de monotonie importantes.
?Dérivée-Fonction puissance
Énoncé
Soit la fonction \(f\) définie sur \([0;8]\) par \(f(x)=(4- x^{\frac{2}{3}} )^{\frac{3}{2}}\).
Cocher les affirmations vraies.
Correction
Explication Générale
On utilise la propriété relative à la dérivée d'une fonction puissance
?Dérivée-Fonction puissance
Énoncé
Soit la fonction \(h\) définie par \(h(x) = e^x 2^{x+1}\)
Cocher les affirmations vraies.
Correction
?Transformation
Énoncé
Coche la ou les bonne(s) réponse(s)
Correction
?Divisibilité
Énoncé
Soit l'entier naturel \(N = 5^6\,n + 1 + 2^3\,n + 1\) où \(n\) est un entier naturel.
Correction
?Divisibilité
Énoncé
Le nombre \(1785^{2012}\)
Correction
?Divisibilité
Énoncé
Si \(n\) est un entier pair, alors \(7^{n+ 1}\) est divisible par 8.
Correction
?Divisibilité
Énoncé
Soit \(x \in \mathbb{Z}\), si \(x^2 \equiv -1 \pmod{5}\), alors
Correction
?Divisibilité
Énoncé
Coche la ou les bonne(s) réponse(s)
Correction
?Equations dans Z
Énoncé
Combien y-a -t-il de couples \((x,y)\) d'entiers relatifs solutions de l'équation :\( x^2-y^2 = 10\) ?
Correction
?Equations dans Z
Énoncé
Le couple \((3 ; -1)\) est solution particulière de l'équation : \(12x + 35y = 1.\)
On a :
Correction
?Equations dans Z
Énoncé
Laquelle des propositions suivantes est exacte?
Correction
?Equations dans Z
Énoncé
L'équation \(6x – 8y = 1\) dans \(\mathbb{Z}^2\) admet :
Correction
?Equations dans Z
Énoncé
L'équation \(37x + 23y = 1\) dans \(\mathbb{Z}^2\) admet :
Correction
?Equations dans Z
Énoncé
L'équation \(1665x + 1035y = 45\) dans \(\mathbb{Z}^2\) admet :
Correction
?Equations dans Z
Énoncé
Cochez les bonnes réponses
Correction
?Equations dans Z
Énoncé
L'équation \(12x + 7y = 2\) dans \(\mathbb{Z}^2\) admet :
Correction
?Equations dans Z
Énoncé
L'équation \(3x + 5y = 4\pmod{7}\) dans \(\mathbb{Z}\) admet :
Correction
?Divisibilité - nombres premiers
Énoncé
Cochez les bonnes réponses
Correction
Explication Générale
Un nombre entier premier n'est pas premier avec tous les entiers qu'il divise.
?Divisibilité - nombres premiers
Énoncé
Cochez les bonnes réponses
Correction
Explication Générale
Un nombre entier premier n'est pas premier avec tous les entiers qu'il divise.
?Divisibilité - nombres premiers
Énoncé
Cochez les bonnes réponses
Correction
Explication Générale
L'ensemble des nombres premiers est infini.
?Divisibilité - nombres premiers
Énoncé
Cochez les bonnes réponses
Correction
Explication Générale
Deux nombres sont premiers entre eux si leur pgcd vaut 1
?Divisibilité - nombres premiers
Énoncé
Cochez les bonnes réponses
Correction
Explication Générale
Deux nombres sont premiers entre eux si leur pgcd vaut 1
?Divisibilité - nombres premiers
Énoncé
Cochez les bonnes réponses
Correction
?Divisibilité - nombres premiers
Énoncé
Cochez les bonnes réponses
Correction
?Divisibilité - nombres premiers
Énoncé
Cochez les bonnes réponses
Correction
?Divisibilité - nombres premiers
Énoncé
Cochez les bonnes réponses
Correction
?Divisibilité - nombres premiers
Énoncé
Cochez les bonnes réponses
Correction
?Intégrale de produit de fonctions
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(D=\int_2^0(x-2)^2e^x~dx\)
Correction
?Intégrale de produit de fonctions
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(E=\int_0^\pi e^t\sin t~dt\)
Correction
?Intégrale de produit de fonctions
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(F=\int_0^{\frac{\pi}{3}}x\frac{\sin x}{\cos^3(x)}~dx\)
Correction
?Intégrale de produit de fonctions
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(G=\int_0^{\frac{\pi}{2}}\sin^2(x)\cos^5(x)~dx\)
Correction
?Intégrale de produit de fonctions
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(G=\int_0^{\frac{\pi}{2}}\sin(x)\cos^3(x)~dx\)
Correction
?Intégrale de produit de fonctions
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(G=\int_0^{\frac{\pi}{2}}\sin(x)\cos(x)~dx\)
Correction
?Intégrale de produit de fonctions
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(G=\int_1^e\ln x~dx\)
Correction
?Intégration par parties
Énoncé
\((D)\) est l'ensemble des points \(M(x , y)\) du plan tels que : \(\left \{\begin{array}{rcl} 1 \leq x \leq e \\ 0 \leq y \leq \frac{1}{x} \end{array}\right.\). L'unité graphique est \(3\) cm. L'aire de \((D)\) en \(cm^2\) est :
Correction
?Intégrales et aires
Énoncé
\((D)\) est l'ensemble des points \(M(x , y)\) du plan tels que : \(\left \{\begin{array}{rcl} 1 \leq x \leq e \\ 0 \leq y \leq \frac{1}{x} \end{array}\right.\). L'aire de \((D)\) en unités d'aires est :
Correction
?Intégrales et aires
Énoncé
\((D)\) est l'ensemble des points \(M(x , y)\) du plan tels que : \(\left \{\begin{array}{rcl} 1 \leq x \leq e \\ 0 \leq y \leq \frac{1}{x}ln(x) \end{array}\right.\). L'unité graphique est 3 \(cm\). L'aire de \((D)\) en unités d'aire est :
Correction
?Intégrales et aires
Énoncé
\((D)\) est l'ensemble des points \(M(x , y)\) du plan tels que : \(\left \{\begin{array}{rcl} -2 \leq x \leq 0 \\ 0 \leq y \leq x^3+2x^2+2x+4 \end{array}\right.\). L'aire de \((D)\) en unités d'aire est :
Correction
?Intégrales et aires
Énoncé
Considérons les fonctions \(f\) et \(g\) définies sur \([1 ;5]\) par : \(f(x)=x^2+\frac{4}{x^2}\) et \(g(x)=x^2\). \((C_f)\) et \((C_g)\) les courbes respectives de \(f\) et \(g\) dans un repère orthonormal du plan. L'unité graphique est 1 \(cm\). L'aire en \(cm^2\) comprise entre \((C_f)\) et \((C_g)\) sur \([1 ;5]\) est :
Correction
?Intégrales et aires
Énoncé
Considérons la fonction \(f\) définie sur \([-3 ;-2]\) par : \(f(x)=\frac{x^2-7x+10}{2(1-x)}\) et \((C_f)\) sa courbe représentative dans un repère orthonormal du plan. L'unité graphique est 2 \(cm\). L'aire en \(cm^2\) comprise entre \((C_f)\), l'axe des abscisses et les droites d'équations : \(x=-3\) et \(x=-2\) est :
Correction
?Intégrales et aires
Énoncé
Considérons la fonction \(f\) définie sur \([0 ;+\infty[\) par : \(f(x)=\frac{x^2}{2}(lnx-\frac{3}{2})\) si \(x >0\) et \(f(0)=0\). \((C_f)\) sa courbe dans un repère orthonormal du plan. L'unité graphique est \(2~cm\). L'aire en \(cm^2\) comprise entre \((C_f)\), l'axe des abscisses et les droites d'équations \(x=\alpha\), \(\alpha >0\) et \(x=e\) est :
Correction
?Intégrales et aires
Énoncé
Considérons la fonction \(f\) définie sur \([0 ;+\infty[\) par \(f(x)=\frac{x^2}{2}(lnx-\frac{3}{2})\) si \(x>0\) et \(f(0)=0\). \((C_f)\) sa courbe dans un repère orthonormal du plan. L'unité graphique est \(2\) \(cm\). L'aire en \(cm^2\) comprise entre \((C_f)\), l'axe des abscisses et les droites d'équations \(x=0\) et \(x=e\) est :
Correction
?Intégrales de fonctions puissances
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(A=\int_1^2x^6~dx\)
Correction
?Intégrales de fonctions puissances
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(A=\int_0^{\frac{\pi}{6}}\sin^3 (2x)~dx\)
Correction
?Intégrales et moyenne
Énoncé
Soit la fonction f définie sur \([0 ; \pi]\) par : \(f(x) = sin^2(x)\) . La valeur moyenne de f sur \([0 ; \pi]\) est :
Correction
?Intégrales et moyenne
Énoncé
Soit la fonction \(f\) définie sur \([1 ; 4]\) par : \(f(x) = x^2 - 1\). La valeur moyenne de\( f\) sur \([1 ; 4\)] est :
Correction
?Intégrales et moyenne
Énoncé
Soit la fonction \(f\) définie sur \([0 ; \pi]\) par : \(f(x) = x - sinx\). La valeur moyenne de \(f\) sur \([0 ; \pi]\) est :
Correction
?Intégrales et moyenne
Énoncé
Soit la fonction f définie sur \([0 ; \frac{\pi}{2}]\) par : \(f(x) = sin^2 (x) cos^5(x)\). La valeur moyenne de\( f\) sur \([0 ; \frac{\pi}{2}]\) est :
Correction
?Intégrales et moyenne
Énoncé
Soit la fonction \(f\) définie sur \([0 ;1]\) par :\( f(x) = x^2 e^x\). La valeur moyenne de \(f\) sur \([0 ; 1]\) est :
Correction
?Intégrales et moyenne
Énoncé
Soit la fonction \(f\) définie sur \([0 ; \pi]\) par : \(f(x) = e^x sinx\). La valeur moyenne de \(f\) sur \([0 ; \pi]\) est :
Correction
?Intégrales simples
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(C=\int_0^{\frac{\pi}{3}}\cos (x)\sin^4{(x)} dx\)
Correction
?Intégration par parties
Énoncé
Soit \(\int_0^1x^2e^x ~dx\). Coche la bonne réponse
Correction
?Intégration par parties
Énoncé
Soit \(\int_{-1}^0(2x+1)e^{-x}~ dx\). Coche la bonne réponse.
Correction
?Produit mixte
Énoncé
Le produit mixte est antisymétrique
Correction
?Produit mixte
Énoncé
Le réel\(\| (\overrightarrow{AB} \wedge \overrightarrow{AC}) \cdot \overrightarrow{AD}\| \) est le volume du parallélépipède \(ABCDEFGH\)
Correction
?Produit mixte
Énoncé
Le réel \(\|\overrightarrow{AB} \wedge \overrightarrow{AC} \|\) est l'aire du triangle ABC
Correction
?Produit vectoriel
Énoncé
Si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont deux vecteurs non nuls alors (\(\overrightarrow{u}\), \(\overrightarrow{v}\), \(\overrightarrow{u}\)∧\(\overrightarrow{v}\)) est une base directe de l'espace des vecteurs
Correction
?Produit vectoriel
Énoncé
Si \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont deux vecteurs non nuls orthogonaux alors (\(\overrightarrow{u}\), \(\overrightarrow{v}\), \(\overrightarrow{u}\)∧\(\overrightarrow{v}\)) est une base orthonormale directe de l'espace des vecteurs.
Correction
?Produit vectoriel
Énoncé
Le produit vectoriel est commutatif
Correction
?Produit vectoriel
Énoncé
Soient \(A, B, C\) trois points non alignés. Le vecteur\( \overrightarrow{AB}\) \(\wedge\) \(\overrightarrow{AC}\) est un vecteur directeur du plan\( (ABC)\)
Correction
?TRANSFORMATIONS ELEMENTAIRES DE L'ESPACE
Énoncé
Soit \((P)\) un plan de l'espace et \(S_P\) la réflexion de plan \((P)\) .
Soit \(A\) et \(B\) deux points de l'espace.
B= \(S_P (A)\) si et seulement si\( (P)\) est le plan médiateur de\( [AB]\)
Correction
?TRANSFORMATIONS ELEMENTAIRES DE L'ESPACE
Énoncé
Soit \((P)\) un plan de l'espace et \(S_P\) la réflexion de plan \((P)\) .
Pour tout point \(M\) de l'espace, \(S_P (M)=M \iff P\) est invariant par \(S_P\).
Correction
?TRANSFORMATIONS ELEMENTAIRES DE L'ESPACE
Énoncé
Soit \((P)\) un plan de l'espace et \(S_P\) la réflexion de plan\( (P)\) .
Si \(B= S_P (A)\) . alors \(\overrightarrow{AB}\) est un vecteur normal de \((P).\)
Correction
?TRANSFORMATIONS ELEMENTAIRES DE L'ESPACE
Énoncé
Soit \((P)\) un plan de l'espace et \(S_P\) la réflexion de plan\( (P)\) .
Si \(B= S_P (A)\) . alors, si B=\( S_P (A)\) . alors \(\overrightarrow{AB}\) est un vecteur directeur de \((P)\).
Correction
?TRANSFORMATIONS ELEMENTAIRES DE L'ESPACE
Énoncé
5. Soit \((P)\) un plan de l'espace et \(S_P\) la réflexion de plan \((P)\) .
\((S_P)^{-1}= S_P\) où \((S_P)^{-1}\) est la transformation réciproque de la transformation \(S_P\)
Correction
?TRANSFORMATIONS ELEMENTAIRES DE L'ESPACE
Énoncé
Soit \((P)\) et \((P')\) deux plans de l'espace,\( S_P\) et \(S_{P'}\) les réflexions de plan respectifs \((P)\) et \((P')\).
Si les plans \((P)\) et \((P'\)) sont parallèles alors la composée \(S_{P'} \circ S_P\) est une translation de vecteur normal aux plans\( (P)\) et\( (P')\)
Correction
?TRANSFORMATIONS ELEMENTAIRES DE L'ESPACE
Énoncé
Soit \((P)\) et \((P')\) deux plans de l'espace,\( S_P\) et \(S_{P'}\) les réflexions de plan respectifs \((P)\) et \((P')\).
Si les plans \((P)\) et \((P'\)) sont sécants suivant une droite \((\Delta)\) alors la composée \(S_{P'} \circ S_P\) est une rotation autour de \((\Delta)\)
Correction
?TRANSFORMATIONS ELEMENTAIRES DE L'ESPACE
Énoncé
Soit \((P)\) et \((P')\) deux plans de l'espace,\( S_P\) et \(S_{P'}\) les réflexions de plan respectifs \((P)\) et \((P')\). \((S_{P'} \circ S_{P})^{-1}=(S_{P'})^{-1} \circ (S_{P})^{-1}\)
Correction
?TRANSFORMATIONS ELEMENTAIRES DE L'ESPACE
Énoncé
Soit \(h\) l'homothétie de centre\( A(0 ;1 ;-1)\) et de rapport \(-4\), \(t\) la translation de vecteur\( \overrightarrow{u}(-2 ;1 ;1).\)
Correction
?TRANSFORMATIONS ELEMENTAIRES DE L'ESPACE
Énoncé
Soit \(h\) l'homothétie de centre\( A(0 ;1 ;-1)\) et de rapport \(-4\), \(t\) la translation de vecteur\( \overrightarrow{u}(-2 ;1 ;1).\)
Correction
?TRANSFORMATIONS ELEMENTAIRES DE L'ESPACE
Énoncé
Cpche la ou les bonne(s) réponse(s)
Correction
?TRANSFORMATIONS ELEMENTAIRES DE L'ESPACE
Énoncé
Coche la ou les bonne(s) réponse(s)
Correction
?Calcul barycentrique
Énoncé
On considere un triangle \(ABC\) tel que \(AB = 7\),\( BC = 4\) et \(AC = 5\). \(I\) est le milieu de \([BC]\). L'ensemble des points \(M\) tels que : \(-2 MA^2+ MB^2+ MC^2=-58\) est :
Correction
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit deux vecteurs \( \overrightarrow{v_1}\) et \(\overrightarrow{v_2}\) dans l'espace, de coordonnées respectives \((v_{1,x}, v_{1,y}, v_{1,z})\) et \((v_{2,x}, v_{2,y}, v_{2,z})\).
Comment s'exprime le produit scalaire \(\overrightarrow{v_1}.\overrightarrow{v_2}\) ?
Correction
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On considère deux vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{AC}\) de norme non nulle.
Quelles propositions permettent de compléter de manière juste la phrase suivante "Un produit scalaire entre deux vecteurs \(\overrightarrow{AB}\) et \(\overrightarrow{AC} ...\)" ?
Correction
Explication Générale
Le produit scalaire \(\overrightarrow{u}. \overrightarrow{v} = ||\overrightarrow{u}||. ||\overrightarrow{v} ||. \cos(( \overrightarrow{u}, \overrightarrow{v}))\).
Le résultat est un nombre réel (appelé aussi “scalaire”) qui peut prendre des valeurs positives comme des valeurs négatives ou nulles.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On considère deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) de norme non nulle. On appelle angle \(\alpha\) l'angle non orienté entre les vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\).
Dans quel(s) cas a-t-on le produit scalaire \(\overrightarrow{u}.\overrightarrow{v}\) égal à 0 ?
Correction
Explication Générale
Le produit scalaire \(\overrightarrow{u}.\overrightarrow{v}\) est donné par \(\overrightarrow{u}.\overrightarrow{v} ) = ||\overrightarrow{u}|| ||\overrightarrow{v} || \cos((\overrightarrow{u}, \overrightarrow{v})) \).
Comme \(\overrightarrow{u}\) et \(\overrightarrow{v}\) sont de norme non nulle, le seul cas où le produit scalaire s'annule est le cas où \(\cos((\overrightarrow{u}, \overrightarrow{v})) = 0\), c'est-à-dire le cas où les deux vecteurs sont orthogonaux.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient deux vecteurs \(\overrightarrow{v}\) et \(\overrightarrow{w}\) de coordonnées respectives \(\begin{pmatrix}v_x\\v_y\\v_z\end{pmatrix}\) et \(\begin{pmatrix}w_x\\w_y\\w_z\end{pmatrix}\) dans \(R^3\).
Quelles sont, par définition, les coordonnées du vecteur \(\overrightarrow{u}= \overrightarrow{v} + \overrightarrow{w}\) ?
Correction
Explication Générale
À savoir : Les coordonnées de \(\overrightarrow{u}=\overrightarrow{v}+\overrightarrow{w}\) sont donnés par : \(\begin{pmatrix}v_x + w_x\\v_y+w_y\\v_z + w_z\end{pmatrix}\).
Voir Ressource Unisciel.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient deux vecteurs \(\overrightarrow{v}\) et \(\overrightarrow{w}\) de coordonnées respectives \(\begin{pmatrix}v_x\\v_y\\v_z\end{pmatrix}\) et \(\begin{pmatrix}w_x\\w_y\\w_z\end{pmatrix}\) dans \(\mathbb{R}^3\).
Quelles sont, par définition de la différence de deux vecteurs, les coordonnées du vecteur \(\overrightarrow{u}= \overrightarrow{v} - \overrightarrow{w}\) ?
Correction
Explication Générale
Les coordonnées de \(\overrightarrow{u}=\overrightarrow{v}-\overrightarrow{w}\) sont donnés par : \(\begin{pmatrix}v_x - w_x\\v_y-w_y\\v_z - w_z\end{pmatrix}\).
Voir http://uel.unisciel.fr/physique/outils_nancy/outils_nancy_ch03/co/apprendre_02_01.html.
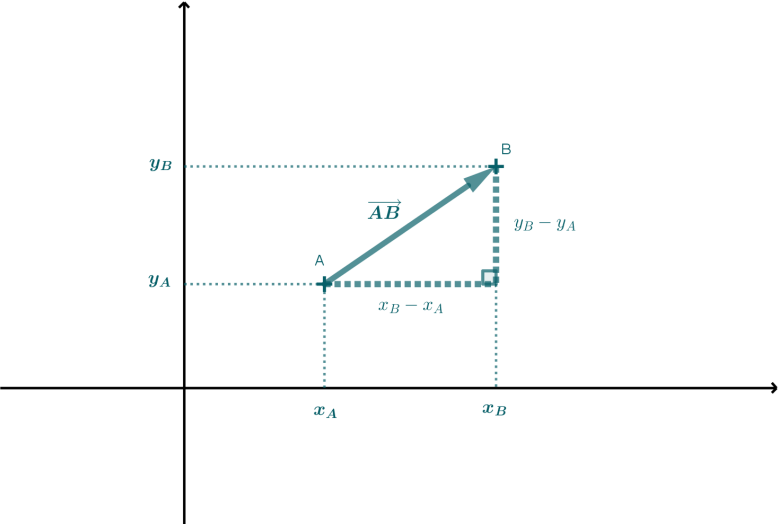
?Représenter une grandeur physique avec un vecteur
Énoncé
Dans un repère orthonormé \((O ;\overrightarrow{i},\overrightarrow{j})\), on donne les points \(A(x_A;y_A)\) et de \(B(x_B;y_B)\).
Donner l'expression de la norme du vecteur \(\overrightarrow{AB}\).
Correction
Explication Générale
La norme d'un vecteur est la longueur de ce vecteur.
D'après le théorème de Pythagore appliqué au triangle rectangle dont l’hypoténuse est le vecteur et les deux autres côtés sont les coordonnées du vecteur, on obtient :
\(|| \overrightarrow{AB}||=\sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}\)
?Isométries du plan
Énoncé
Toute isométrie est une transformation qui conserve les distances.
Correction
?Isometries du plan
Énoncé
Toute isométrie conserve les alignements, les milieux, les intersections.
Correction
?Isométries du plan
Énoncé
Toute transformation est une isométrie
Correction
?Isometries du plan
Énoncé
Toute isométrie conserve le parallélisme et l'orthogonalité.
Correction
?Isométries du plan
Énoncé
Toute isométrie transforme un segment en un segment.
Correction
?Isométries du plan
Énoncé
Toute isométrie conserve le barycentre d'un système de points pondérés.
Correction
?Isométries du plan
Énoncé
Toute isométrie transforme une droite en une droite.
Correction
?Similitudes Planes Directes
Énoncé
Toute similitude de rapport \(k ( k > 0 )\) transforme une droite en une droite.
Correction
?Similitudes Planes Directes
Énoncé
Toute similitude de rapport \(k ( k > 0 )\) multiplie les distances par \(k.\)
Correction
?Similitudes Planes Directes
Énoncé
Toute similitude de rapport \(k ( k > 0 )\) multiplie les aires par\( k\)
Correction
?Similitudes Planes Directes
Énoncé
Toute similitude de rapport k ( k > 0 ) multiplie les aires par k2
Correction
?Similitudes Planes Directes
Énoncé
Toute similitude de rapport \(k ( k > 0 )\) conserve les angles géométriques donc le parallélisme et l'orthogonalité.
Correction
?Similitudes Planes Directes
Énoncé
Toute similitude de rapport \(k ( k > 0 )\) conserve les alignements, les milieux, les intersections.
Correction
?Similitudes Planes Directes
Énoncé
Toute similitude de rapport\( k ( k > 0\) ) transforme un segment en un segment.
Correction
?Similitudes Plaanes Directes
Énoncé
Toute similitude de rapport\( k ( k > 0 )\) conserve le barycentre d'un système de points pondérés.
Correction
?Similitudes Planes Directes
Énoncé
Toute similitude de rapport \(k ( k > 0 )\) transforme un cercle de centre \(O\) et de rayon \(R\) en un cercle de centre l'image de \(O\) par la similitude et de rapport\( k × R\).
Correction
?Similitudes Planes Directes
Énoncé
Toute similitude de rapport \(k ( k > 0\) ) transforme un cercle de centre \(O\) et de rayon \(R\) en un cercle de centre l'image de \(O\) par la similitude et de rapport \(R\).
Correction
?Similitudes Planes Directes
Énoncé
Toute similitude plane directe a une écriture complexe de la forme\( z \to az + b\), où \(a\) et \(b\) sont des complexes tels que \(|a| = k.\)
Correction
?Similitudes Planes Directes
Énoncé
Le plan est rapporté au repère orthonormal direct \((O; \overrightarrow{u}; \overrightarrow{v}),\) on considère l'application\( f\), du plan dans lui –même, qui à tout point \(M\) daffixe \(z\) associe le point\( M'\) d'affixe \(z'\) tel que : \(z' =(1+i\sqrt{3})z - i\sqrt{3}.\)
Coche la bonne réponse
Correction
?Similitudes Planes Directes
Énoncé
Le plan est rapporté au repère orthonormal direct \((O; \overrightarrow{u}; \overrightarrow{v}),\) on considère l'application \(f\), du plan dans lui –même, qui à tout point M d4affixe \(z\) associe le point \(M'\) d'affixe \(z'\) tel que : \(z' =(1+i\sqrt{3} ))z - i\sqrt{3} ).\)
L'image par\( f\) de la droite \((D)\) , d'équation : \(\sqrt{3}x + y = 0\) est :
Correction
?Similitudes Planes Directes
Énoncé
Le plan est rapporté au repère orthonormal direct \((O; \overrightarrow{u}; \overrightarrow{v}),\), on considère l'application \(f\), du plan dans lui –même, qui à tout point \(M\) d'affixe \(z\) associe le point \(M'\) d'affixe \(z'\) tel que : \(z' =(1+i\sqrt{3})z - i\sqrt{3}\).
L'image par \(f\) du cercle\( (C)\) de centre \(O\) et de rayon 2 est :
Coche la bonne réponse
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
\(ABCD\) est un carré direct de centre \(O\).
La transformation f définie par : \(f=S_{(AC)} \circ S_{(AB)}\) est :
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
\(ABCD\) est un carré direct de centre \(O\).
La transformation f définie par : \(f=S_{(DC)} \circ S_{(AB)}\) est :
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
Le plan est rapporté au repère orthonormal \((O; \overrightarrow{i};\overrightarrow{j} )\), on note \(s\) la symétrie orthogonale d'axe la droite\( (D)\) d'équation: \(x + y\sqrt{3} - 2 = 0\) et \(s'\) la symétrie orthogonale d'axe la droite\( (D')\) d'équation: \( x \sqrt{3}- y+ 2 \sqrt{3}= 0\) .
\(s\circ s'\) est :
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
\(ABCD\) est un carré direct de centre \(O\).
La transformation f définie par : \(f=S_{(AB)} \circ S_{(BC)} \circ S_{(CD)} \circ S_{(DA)}\) est :
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
\(ABCD\) est un carré direct de centre\( O\).
La transformation\( f\) définie par :\( f= r_{(C ;-\frac{\pi}{2})} \circ r_{(A ;\frac{\pi}{2})}\)) est :
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
\(ABCD\) est un carré direct de centre\( O\).
La transformation\( f\) définie par :\( f= r_{(A ;\frac{\pi}{2})} \circ r_{(C ;\frac{\pi}{2})}\)) est :
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
\(ABCD\) est un carré de centre \(O\). La transformation \(f\) définie par : \(f=t_{2\overrightarrow{AD}} \circ r_{(A ;-\frac{\pi}{2})}\)
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
ABCD est un carré direct de centre O.
La transformation \(f\) définie par : \(f= s_{(AC)} \circ r_{(A ;\frac{\pi}{2})}\) est :
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
ABCD est un carré direct de centre O.
La transformation f définie par :\( f=S_{(AB)} \circ S_{(CD)} \circ S_{(BC)} \circ S_{(AD)}\) est :
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
Une similitude directe de centre\( I\) et d'angle nulle est une homothétie de centre \(I\)
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
Une similitude directe de rapport \(1\) est une rotation
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
Une symétrie centrale est une similitude directe.
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
Une homothétie de rapport \(– 2\) est une similitude d'angle nul
Correction
?SYMETRIES ORTHOGONALES- ROTATIONS- TRANSLATIONS
Énoncé
Une similitude directe de rapport \(3\) a un seul point invariant
Correction
?Points cocycliques
Énoncé
4 points \(A, B, C\) et \(D\) d'affixes respectifs, \(a b, c\) et \(d\), 2 à 2 distincts sont cocycliques ou alignés si, et seulement si
Correction
?Points cocycliques
Énoncé
4 points \(A, B, C\) et \(D\) distincts et non alignés sont cocycliques ou alignés si, et seulement si :
Correction
?Points cocycliques
Énoncé
Soient \(A\) et \(B\) 2 points distincts, l'ensemble des points \(M\) du plan tells que : \((\overrightarrow{MA},\overrightarrow{MB})=0 \pmod {2\pi}\) est :
Correction
?Applications dans l'ensemble des nombres complexes
Énoncé
On considère le repère \((O,\overrightarrow{u}; \overrightarrow{v})\) du plan complexe. L'application qui à tout point \(M(z)\) associe le point
\(M'( z')\) tel que : \(z'=(1+i)z+4+4i\) est :
Correction
?Applications dans l'ensemble des nombres complexes
Énoncé
On considère le repère \((O,\overrightarrow{u}; \overrightarrow{v})\) du plan complexe. L'application qui à tout point \(M(z)\) associe le point \(M'( z')\) tel que :\( z'= z-3+4i\) est :
Correction
?Applications dans l'ensemble des nombres complexes
Énoncé
On considère le repère \((O,\overrightarrow{u}; \overrightarrow{v})\) du plan complexe. L'application qui à tout point \(M(z)\) associe le point\( M'( z')\) tel que : \(z'=\overline{z}\) est:
Correction
?Applications dans l'ensemble des nombres complexes
Énoncé
On considère le repère \((O,\overrightarrow{u}; \overrightarrow{v}) \)du plan complexe. L'application qui à tout point \(M(z)\) associe le point \(M'( z')\) tel que : \(z'= -iz+i+3i\) est :
Correction
?Applications dans l'ensemble des nombres complexes
Énoncé
On considère le repère \((O,\overrightarrow{u}; \overrightarrow{v}) \) du plan complexe. L'application qui à tout point\( M(z)\) associe le point \(M'( z')\) tel que : \(z'= -2z\) est :
Correction
?Equations du second degré dans l'ensemble des nombres complexes
Énoncé
L'ensemble solution de l'équation \( z^2 = - 5 +12i\) est
Correction
?Equations du second degré dans l'ensemble des nombres complexes
Énoncé
L'ensemble solution de l'équation : \(z^2+ 4 z+5=0\) est :
Correction
?Equations du second degré dans l'ensemble des nombres complexes
Énoncé
L'équation : \(z^2- 2z\)\(cos(\alpha)+1=0\), \( \alpha \in ]0 ; \pi[\) , a pour solutions :
Correction
?Equations du second degré dans l'ensemble des nombres complexes
Énoncé
L'ensemble solution de l'équation \(z^2=-9\) est:
Correction
?Equations du second degré dans l'ensemble des nombres complexes
Énoncé
L'équation : \(z^2=3\) a pour solutions :
Correction
?Evènements indépendants
Énoncé
Soit \( A\) et \(B\) deux événements d'un univers \(\Omega\). Si \(B\) n'est pas l'événement impossible alors \(A\) et \(B\) sont indépendants si :
Correction
?Evènements indépendants
Énoncé
On lance deux pièces de monnaie et on note la face supérieure. Soit \(A\) : « la première donne FACE » et \(B\) ; « les deux pièces donnent le même résultat
» . La probabilité de « \(A\) et \(B\) » est :
Correction
?Evènements indépendants
Énoncé
Une enquête a révèle que dans un village :
\(20%\) des ménages possèdent au moins un mouton.
\(25%\) des ménages possèdent au moins une chèvre et \(10%\) possèdent au moins un mouton et une chèvre.
La probabilité de « \(A\) et \(B\) » est :
Correction
?Evènements indépendants
Énoncé
On lance une pièce de monnaie non truquée et un dé à 6 faces non pipé.
La probabilité que la pièce tombe sur FACE et que le dé tombe sur 2 est :
Correction
?Evènements indépendants
Énoncé
Un sac contient 5 boules rouges et 3 boules noires. On tire au hasard une boule du sac. Si cette boule est noire, on arrête le jeu ; si cette boule est rouge, on la remet dans le sac, on ajoute deux boules rouges et on procède alors à un deuxième tirage.
La probabilité de tirer deux boules rouges est :
Correction
?Variables aléatoires
Énoncé
On considère un dé cubique truqué dont les faces sont numérotées de 1 à 6 et on note \(X\) la variable aléatoire donnée par le numéro de la face du dessus. On suppose que le dé est truqué de sorte que la probabilité d'obtenir une face est proportionnelle au numéro inscrit sur cette face.
\(E(X)\) est égal à :
Correction
?Variables aléatoires
Énoncé
On lance deux dés parfaitement équilibrés. On note \(X\) le plus grand des numéros obtenus. \(P(X=4)\) est égale à :
Correction
?Variables aléatoires
Énoncé
On considère un dé cubique truqué dont les faces sont numérotées de 1 à 6 et on note \(X\) la variable aléatoire donnée par le numéro de la face du dessus. On suppose que le dé est truqué de sorte que la probabilité d'obtenir une face est proportionnelle au numéro inscrit sur cette face.
\(P(X = 3)\) est égal à :
Correction
?Variables aléatoires
Énoncé
On lance deux dés parfaitement équilibrés. On note \(X\) le plus grand des numéros obtenus.
Correction
?Variables aléatoires
Énoncé
On lance deux dés parfaitement équilibrés. On note \(X\) le plus grand des numéros obtenus.
Correction
?Variables aléatoires
Énoncé
On lance deux dés parfaitement équilibrés. On note \(X\) le plus grand des numéros obtenus.
Correction
?Variables aléatoires
Énoncé
Soit \(X\) une variable aléatoire suivant une loi uniforme discrète sur \({0,1,...,k},\) où a\( k \in \mathbb{N}\). On suppose que\( E(X) = 6\).
Correction
?Variables aléatoires
Énoncé
Dix cyclistes, numérotés de 1 à 10, prennent le départ d'une course. Tous arrivent, il n'y a pas d'ex aequo. Le nombre de classements possibles est :
Correction
?Variables aléatoires
Énoncé
A lance 6 fois un dé parfait et gagne s'il obtient au moins une fois 1.
B lance 12 fois un dé parfait et gagne s'il obtient au moins deux fois 1
Répondre par vrai ou faux :
Correction
?Variables aléatoires
Énoncé
On admet que la probabilité pour qu'un individu pris au hasard soit né sous le signe du Capricorne est égale à \(\frac{1}{12}\).
On considère un groupe de six personnes prises au hasard indépendamment les unes des autres et on note \(X\) la variable aléatoire qui comptabilise le nombre d'individus de ce groupe qui sont nés sous le signe du Capricorne.
La probabilité d'avoir 5 individus qui sont nés sous le signe du Capricorne. Est :
Correction
?Variables aléatoires
Énoncé
On admet que la probabilité pour qu'un individu pris au hasard soit né sous le signe du Capricorne est égale à \(\frac{1}{12}\).
On considère un groupe de six personnes prises au hasard indépendamment les unes des autres et on note \(X\) la variable aléatoire qui comptabilise le nombre d'individus de ce groupe qui sont nés sous le signe du Capricorne.
Correction
?Encadrement d'une suite numérique
Énoncé
La suite numérique définie par : \(U_{n+1} = 1 + \frac{1}{U_n}\) et \(U_0 = 2\) pour tout entier naturel \(n\) est :
Correction
?Encadrement d'une suite numérique
Énoncé
Parmi les affirmations suivantes cocher celles qui sont vraies
Correction
?Encadrement d'une suite numérique
Énoncé
Soit la suite\( (U_n)\) définie sur \(\mathbb{N}\) par : \(U_0=1\) et \(U_{n+1}=\sqrt{2+U_n}\)
Correction
Questions nécessitant un changement de langue
?Question
Énoncé
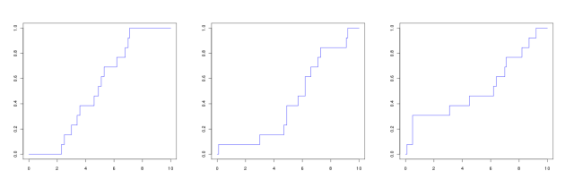
On considère une série statistique à 13 éléments décrite par le diagramme en boîte suivant :
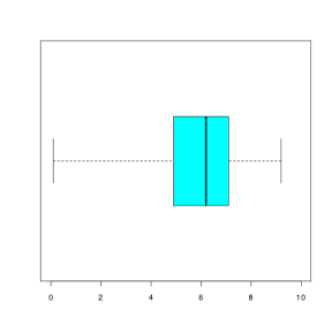
Lequel des graphiques suivants peut correspondre à la courbe de ses fréquences cumulées croissantes ?
Correction
Explication Générale
Notons \(\textstyle{x_1\leq x_2\leq\cdots\leq x_{13}}\) les 13 éléments de la série rangés par ordre croissant. Le minimum de la série est \(\textstyle{x_1}\) , le premier quartile est \(\textstyle{x_4}\) , la médiane est \(\textstyle{x_7}\) , le troisième quartile est \(\textstyle{x_{10}}\) et le maximum est \(\textstyle{x_{13}}\)
D'après le diagramme en boîte, \(\textstyle{x_1}\) est proche de \(\textstyle{0}\) , \(\textstyle{x_4}\) est proche de 5, \(\textstyle{x_7}\) est proche de 6, \(\textstyle{x_{10}}\) est proche de 7 et \(\textstyle{x_{13}}\) est proche de 9.
Le minimum de la série associée au dessin de gauche est supérieur à 2 ; ce ne peut donc être la bonne réponse.
Le premier quartile de la série associée au dessin de droite est proche de 0 ; ce ne peut donc être la bonne réponse.
Le dessin du milieu correspond à la série initiale.
?Question
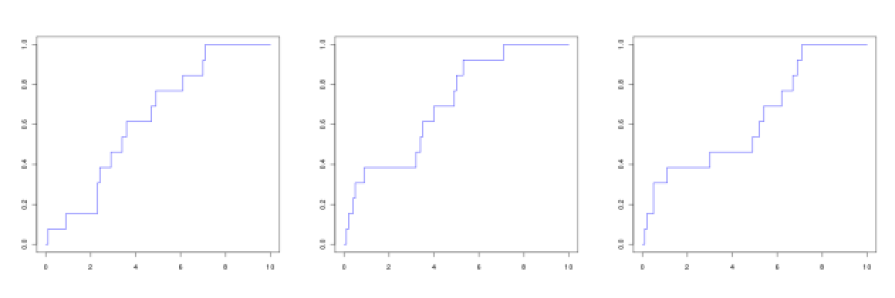
Énoncé
On considère la série statistique à 13 éléments suivante :
\(\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline3.4&2.4&4.9&4.7&7.1&2.9&7.0&0.9&3.6&2.3&6.1&0.1&2.3\\\hline\end{array}\)
Lequel des dessins suivants correspond à sa courbe des fréquences cumulées croissantes ?
Correction
Explication Générale
Les premiers éléments de la série sont \(\textstyle{0.1}\) , \(\textstyle{0.9}\) , \(\textstyle{2.3}\) , \(\textstyle{2.3}\)
Les séries associées aux dessins du milieu et de droite ont 5 éléments inférieurs à 2; elles ne peuvent être la bonne réponse.
Le dessin de gauche correspond à la série initiale.
?Question
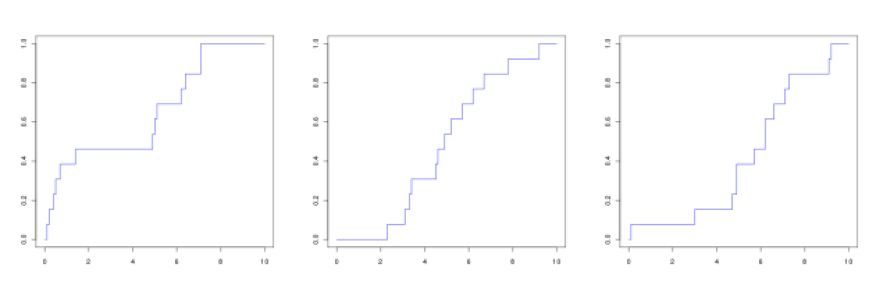
Énoncé
On considère la série statistique à 13 éléments suivante :
\(\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline6.7&3.3&2.3&4.6&6.2&3.4&5.7&5.2&7.8&4.9&3.1&4.5&9.2\\\hline\end{array}\)
Lequel des graphiques suivant peut correspondre à sa courbe des fréquences cumulées croissantes ?
Correction
Explication Générale
Le minimum de la série est \(\textstyle{2.3}\) , le maximum est \(\textstyle{9.2}\)
Le maximum de la série associée au dessin de gauche est inférieur à 8 ; ce ne peut être la bonne réponse.
Le minimum de la série associée au dessin du milieu est proche de 0 ; ce ne peut être la bonne réponse.
Le dessin du milieu correspond à la série initiale.
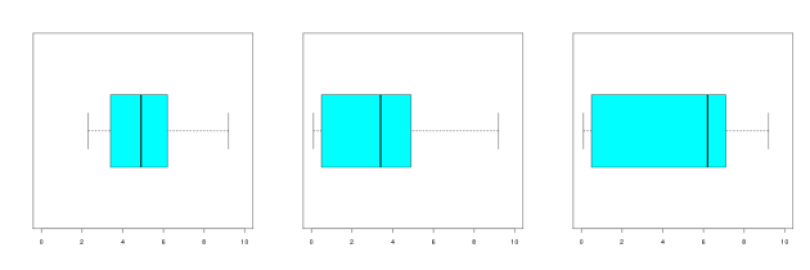
?Question
Énoncé
On considère la série statistique à 13 éléments suivante :
\(\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline0.5&4.5&0.1&8.2&0.5&8.7&3.1&6.4&0.5&6.2&9.2&7.0&7.1\\\hline\end{array}\)
Lequel des graphiques suivant peut correspondre à son diagramme en boîte ?
Correction
Explication Générale
Ordonnons la série :
Le minimum de la série associée au dessin de gauche est supérieur à 2 ; ce ne peut être la bonne réponse.
La médiane de la série associée au dessin de gauche est inférieure à 4 ; ce ne peut être la bonne réponse.
Le dessin de droite correspond à la série initiale.
?Question
Énoncé
Soit un univers muni d'une probabilité \(\textstyle{\mathbb P}\) et \(\textstyle{A}\) et \(\textstyle{B}\) deux événements tels que \(\textstyle{{\mathbb P(A\cap B)=\dfrac13}}\) et \(\textstyle{\mathbb P(A)=\dfrac12}\). Donner la ou les bonnes réponses.
Correction
?Question
Énoncé
Soit un univers muni d'une probabilité \(\textstyle{\mathbb P}\) et \(\textstyle{A}\) et \(\textstyle{B}\) deux événements tels que \(\textstyle{\mathbb P(A)=\dfrac12}\) , \(\textstyle{\mathbb P(B)=\dfrac13}\) et \(\textstyle{\mathbb P(A\cap B)=\dfrac16}\) . Déterminer la ou les bonnes réponses.
Correction
?Question
Énoncé
On lance deux fois un dé non pipé.
Correction
?Question
Énoncé
Si \(\textstyle{A}\) et \(\textstyle{B}\) sont deux événements disjoints alors ils sont toujours indépendants.
Correction
Explication Générale
Deux événements disjoints ne sont indépendants que si l'un deux est de probabilité nulle.
?Question
Énoncé
Le nombre complexe \( \frac{i-2}{1+i}\) est égal à
Correction
Explication Générale
Vous pouvez regarder les ressources suivantes
et en vidéo
Chapitre « Nombres complexes » - Partie 1 définitions et opérations
?Question
Énoncé
On note \(\alpha\) le nombre complexe \(\alpha=-\sqrt{3}+i\). On a
Correction
Explication Générale
Vous pouvez regarder les ressources suivantes
et en vidéo
Nombres réels – Partie 1 : nombres rationnels
Nombres réels – Partie 2 : Propriété des réels
Chapitre « Nombres complexes » - Partie 1 définitions et opérations
Chapitre « Nombres complexes » - Partie 2 : racines carrées, équations du second degré
?Question
Énoncé
La courbe représentative de la fonction \(f:x \mapsto \frac{\ln(x)}{x}\) a l'allure
Correction
Explication Générale
Voici deux ressources pour revoir quelques notions :
?Question
Énoncé
Soit \(f\) une fonction définie sur \(\mathbb{R}\). Que signifie "\(f(x)\) tend vers + l'infini lorsque \(x\) tend vers + l'infini" :
Correction
Explication Générale
Attention, si \(\lim\limits_{x\to+\infty}f(x)=+\infty\), alors \(f\) n'est pas majorée, mais la réciproque est fausse : par exemple, \(x\sin{x}\) n'est pas majorée, mais ne tend pas vers plus l'infini.
Le fait que \(\lim\limits_{x\to+\infty}f(x)=+\infty\) n'implique pas que \(f\) soit strictement croissante, et le fait que \(f\) soit strictement croissante n'implique pas \(\lim\limits_{x\to+\infty}f(x)=+\infty\) : ces deux propriétés n'ont rien à voir.
La réponse 3) est la bonne, c'est la définition de tendre vers plus l'infini quand \(x\) tend vers plus l'infini.
La réponse 4) n'a pas de sens : pour tout \(x\), \(f(x)\) est un réel, donc ne vaut pas \(+\infty\).
Voici une ressource pour revoir quelques notions :
?Question
Énoncé
Soit \(f\) une fonction. La bonne définition de la propriété "La fonction \(f\) est croissante sur l'intervalle \([a,b]\)" est
Correction
Explication Générale
La réponse 1) est fausse car si \(f\) est croissante, alors \(f(a)\leq f(b)\), mais la réciproque est fausse : par exemple, \(\sin(0)\leq \sin(5\pi/2)\), mais \(\sin\) n'est pas croissante sur tout l'intervallle \([0,5\pi/2]\). Cela montre aussi que la définition 4) est fausse. 2) n'est pas assez précis, bien que cela soit vrai que la courbe monte, il faut se mettre d'accord sur le sens de monter, et avoir adopté un système de coordonnées où l'axe \(y\) est orienté vers le haut, bref cela repose sur des sous-entendus et n'est pas une bonne définition. La réponse 3) est la bonne définition.
Voici une ressource pour revoir quelques notions :
?Question
Énoncé
Complétez l'assertion suivante afin de former un théorème.
Soit \(f\) une fonction définie et continue sur un intervalle \([a,b]\) de \(\mathbb{R}\).
Correction
Explication Générale
La proposition 1) est fausse : il se peut très bien que pour un certain \(c\in[a,b]\), \(f(c)\) soit hors de l'intervalle \([f(a),f(b)]\).
La proposition 2) est fausse car on n'est même pas sûr que \(f(y)\) ait un sens : encore faut-il que \(y\) soit compris entre \(a\) et \(b\), ce qui n'a aucune raison d'être vrai.
La proposition 3) est vraie, c'est une formulation du théorème des valeurs intermédiaires.
La proposition 4) est fausse, un contre-exemple classique est la fonction valeur absolue, continue mais pas dérivable en zéro.
Voici une ressource pour revoir quelques notions :
?Question
Énoncé
Une urne contient 5 boules blanches et 5 boules noires indiscernables au toucher. On extrait simultanément 3 boules de celle-ci. La probabilité d'avoir exactement 3 boules blanches vaut :
Correction
Explication Générale
Il s'agit de déterminer d'abord l'univers des possibles : \(\binom{9}{3}\) ici car le tirage est simultané .
Pour approfondir vous pouvez consulter cette ressource Probabilités et statistiques
?Question
Énoncé
Le nombre complexe \(-2e^{-i\frac{\pi}{3}}\) a pour
Correction
Explication Générale
Ne pas oublier que le module est un réel positif ou nul. Donc, pour tout nombre complexe \(z\), \(|z|>0\) et \(e^{i\pi}=-1\)
?Question
Énoncé
Soient A,B et C les trois points d'affixes respectives : \(z_A=1+i\), \(z_B=1-i\) et \(z_C=\sqrt{2}e^{i\frac{\pi}{3}}\) . Ces points sont :
Correction
Explication Générale
Le module d'un nombre complexe z est la distance à l'origine du point d'affixe z.
?Question
Énoncé
Dans un plan complexe muni du repère orthonormé \((O ;\vec u ; \vec v)\), pour tout point \(M\) du plan d'affixe \(z\) non nul, si \(arg(z)\) est une mesure en radian de \((\vec u, \overrightarrow{OM})\), alors :
Correction
?Question
Énoncé
Soit \(A\) le point d'affixe \(2i\) et \(B\) le point d'affixe \(-5\) . L'ensemble de tous les points \(M\) d'affixe \(z\) tel que \(|z − 2i| = |z + 5|\) est :
Correction
?Question
Énoncé
Soit \(f\) une fonction continue sur \(\mathbb R\). Soit \(a<b\) deux réels.
Correction
Explication Générale
L'affirmation "Pour tout \(x\geq b\), on a \(\int_a^x f(t)dt\geq \int_a^b f(t)dt\)" est fausse en général : en effet, en utilisant la relation de Chasles, on a \(\displaystyle\int_{a}^{x}f(t)dt-\int_{b}^{x}f(t)dt=\int_{a}^{x}f(t)dt+\int_{x}^{b}f(t)dt=\int_{a}^{x}f(t)dt\). Or dans l'énoncé rien ne permet de connaître le signe du réel \(\int_{a}^{b}f(t)dt\) (par exemple ce réel sera négatif si la fonction \(f\) est négative sur l'intervalle \([a; b]\)).
L'affirmation "La fonction \(x \mapsto \int_a^x f(t)dt-\int_b^xf(t)dt\) est constante sur \(\mathbb R\)" est vraie : en utilisant la relation de Chasles, on trouve que pour tout \(x\in\mathbb R\) on a \(\displaystyle\int_{a}^{x}f(t)dt-\int_{b}^{x}f(t)dt=\int_{a}^{x}f(t)dt+\int_{x}^{b}f(t)dt=\int_{a}^{b}f(t)dt\) qui est bien une constante indépendante de la variable \(x\).
L'affirmation "La primitive de \(f\) qui s'annule en \(a\) est la fonction \(x\mapsto \int_x^bf(t)dt -\int_a^bf(t)dt\)" est fausse. Par la relation de Chasles, on a \(\displaystyle\int_{x}^{b}f(t)dt-\int_{a}^{b}f(t)dt=\int_{x}^{b}f(t)dt+\int_{b}^{a}f(t)dt=\int_{x}^{a}f(t)dt\). Par le théorème fondamental de l'intégration, si \(F\) est une primitive de \(f\), on a \(\int_{x}^{a}f(t)dt=F(a)-F(x)\). Or la primitive de \(f\) qui s'annule en a est la fonction \(x\mapsto F(x)-F(a)\). Ces deux fonctions sont différentes (elles sont opposées), donc l'affirmation est fausse.
L'affirmation "La fonction \(x\mapsto \int_a^bf(t)dt -\int_x^af(t)dt\) est une primitive de \(f\) est juste : là encore, par la relation de Chasles, on obtient \(\displaystyle\int_{a}^{b}f(t)dt-\int_{x}^{a}f(t)dt=\int_{a}^{b}f(t)dt+\int_{a}^{x}f(t)dt\). Si \(F\) est une primitive de \(f\) sur \(\mathbb R\), on a par le théorème fondamental de l'intégration la formule \(\int_{a}^{x}f(t)dt=F(x)-F(a)\), donc on a finalement \(\displaystyle\int_{a}^{b}f(t)dt-\int_{x}^{a}f(t)dt=F(x)-F(a)+\int_{a}^{b}f(t)dt=F(x)+K\), où \(K=-F(a)+\int_{a}^{b}f(t)dt\) est une constante (indépendante de la variable \(x\)). La fonction \(x\mapsto F(x)+K\) est donc bien une primitive de \(f\).
?Question
Énoncé
Soit \(f\) et \(g\) deux fonctions continues sur \(\mathbb R\), et \(a\), \(b\), \(c\) trois réels.
Correction
Explication Générale
L'affirmation "On a \(3\int_a^bf(t)dt=\int_{3a}^{3b}f(t)dt\) est fausse : en effet, si on note \(F\) une primitive de \(f\), on a \(3\int_{}^{b}f(t)dt=3(F(b)-F(a))\), tandis que \(\int_{3a}^{3b}f(t)dt=F(3b)-F(3a)\) : Ces deux quantités sont en général différentes.
Prenons un contre-exemple, en posant \(f(x)=x,\ a=0\;\mathrm{et}\; b= 1\). Une primitive de \(f\) est la fonction \(F(x)=\frac{x^2}{2}\) , et on a \(3(F(1)-F(0))=\frac32\neq F(3)-F(0)=\frac 92\) .
L'affirmation "On a \(3\int_a^b f(t)dt-\int_a^c g(t)dt = \int _a^b(3f(t)-g(t))dt+\int_c^bg(t)dt\)" est juste. On le montre en utilisant la relation de Chasles et la linéarité de l'intégrale : on a \(\displaystyle3\int_{a}^{b}f(t)dt-\int_{a}^{c}g(t)dt=\int_{a}^{b}3f(t)dt-\left(\int_{a}^{b}g(t)dt+\int_{b}^{c}g(t)dt\right)\), ce qui est égal, toujours par linéarité de l'intégrale, à \(\displaystyle\int_{a}^{b}\left(3f(t)-g(t)\right)dt-\int_{b}^{c}g(t)dt=\int_{a}^{b}\left(3f(t)-g(t)\right)dt+\int_{c}^{b}g(t)dt\).
L'affirmation "On a \(3\int_a^b f(t)dt+\int_{-a}^{-b}(t)dt=\int_a^b(3f(t)-g(t))dt\)" est fausse : on a bien l'égalité \(\displaystyle3\int_{a}^{b}f(t)dt=\int_{a}^{b}3f(t)dt\) par linéarité de l'intégrale, mais par contre les deux expressions \(\int_{-a}^{-b}g(t)dt\quad\mathrm{et}\quad-\int_{a}^{b}g(t)dt\) sont en général différentes :
si on note \(G\) une primitive de \(g\), la 1ère expression est égale à \(G(-b)-G(-a)\) tandis que la 2ème est égale à \(-(G(b)-G(a))\). Par exemple, considérons la fonction \(g(t)=e^t\), dont une primitive est
\(G(t)=e^t\), et posons \(a=0\) et \(b=\ln(2)\). On a \(\displaystyle\int_{-a}^{-b}g(t)dt=G(-b)-G(-a)= e^{-\ln(2)}-1=\frac12-1=-\frac12\), tandis que \(\displaystyle-\int_{a}^{b}g(t)dt=-(G(b)-G(a))=-(e^{\ln(2)}-1)= -(2-1)=-1\).
Enfin l'affirmation "On a \(\int_a^b f(t)g(t)dt=\Bigg(\int_a^bf(t)dt \Bigg) \Bigg( \int_a^bg(t)dt\Bigg)\)" est fausse elle aussi, l'intégrale du produit de deux fonctions n'a en général rien à voir avec le produit des intégrales de chacune des deux fonctions. Prenons par exemple les fonctions \(f(t)=g(t)=t\), et \(a=0\; , b=1\). On a alors \(\displaystyle\int_{a}^{b}f(t)g(t)dt=\int_{0}^{1}t^2dt=\left[\frac{t^3}{3}\right]_{0}^{1}=\frac13\) tandis que \(\displaystyle\left(\int_{a}^{b}f(t)dt\right)\left(\int_{a}^{b}g(t)dt\right)=\left(\int_{0}^{1}tdt\right)^2=\left(\left[\frac{t^2}{2}\right]_{0}^{1}\right)^2=\frac14\) .
?Question
Énoncé
On note \(I=\displaystyle\int_x^y 2te^{-kt}dt-2\int_{x/2}^yte^{-kt}dt\). Après calculs, l'intégrale \(I\) dépendra uniquement de
Correction
Explication Générale
La réponse correcte est : \(x\) et \(k\).
On peut ici utiliser la relation de Chasles et la linéarité de l'intégrale pour simplifier l'écriture de \(I\). On obtient :
\(I=\displaystyle \int_x^y 2te^{-kt}dt-2\int_{x/2}^yte^{-kt}dt=2\int_x^yte^{-kt}dt+2\int_y^{x/2}te^{-kt}dt=2\int_x^{x/2}te^{-kt}dt.\)
On en déduit que \(I\) ne dépend pas de la variable \(y\), ce qui montre que les affirmations : "\(x\) et \(y\)", "\(k\), \(y\) et \(t\)" et "\(k\), \(y\) et \(t\)"sont fausses.
L'affirmation "\(x\) et \(k\)" est juste : \(I\) ne dépend pas de la variable muette d'intégration (qui ici est notée \(t\)), mais dépend bien de \(x\) (qui apparaît dans les bornes de l'intégrale) et de \(k\) (qui apparaît comme un paramètre dont dépend la fonction que l'on intègre).
?Question
Énoncé
Soit la proposition "La probabilité de tout événement est inférieur ou égale à \(1\)". La négation de cette proposition est
Correction
?Question
Énoncé
Soit l'assertion "La probabilité de tout événement est inférieure ou égale à \(1\)". La négation de cette assertion est :
Correction
Explication Générale
La négation d'une assertion de la forme \(\forall x \in E, P(x)\) est \(\exists x \in E,\mbox{ non}(P(x))\). La négation de l'assertion proposée exprime le fait qu'il existe au moins un événement dont la probabilité est strictement supérieure à 1.
?Espaces vectoriels
Énoncé
Soit \(E\) un \(\mathbb{R}\)-espace vectoriel non nul et \(F\) et \(G\) deux sous-espaces vectoriels de \(E\) tels que \(F\nsubseteq G\) et \(G\nsubseteq F\). Quelles sont les assertions vraies ?
Correction
Explication Générale
La somme, l'intersection et le produit cartésien de sous-espaces vectoriels est un espace vectoriel. Par contre, la réunion de deux sous-espaces vectoriels n'est un espace vectoriel que si l'un des deux est inclus dans l'autre.
?Applications linéaires
Énoncé
On note \(\mathbb{R}_n[X]\) l'espace des polynômes à coefficients réels de degré \(\le n\), \(n\in \mathbb{N}\). On considère les deux applications suivantes : \(\begin{array}{rccc}f:&\mathbb{R}_3[X]&\to&\mathbf{R}\\& P&\to &P(0)+P'(0)\, \end{array} \quad \mbox{et} \quad \begin{array}{rccc}g:&\mathbb{R}_3[X]&\to&\mathbb{R}_2[X]\\& P&\to &1+P'+XP''\end{array}\)
où \(P'\) (resp. \(P''\)) est la dérivée première (resp. seconde) de \(P\). Quelles sont les assertions vraies ?
Correction
Explication Générale
On vérifie que \(f\) est linéaire. En effet, si \(\lambda, \mu\in\mathbb{R}\) et \(P,Q\in \mathbb{R}_3[X]\) alors \(f(\lambda P+\mu Q)=(\lambda P+\mu Q)(0)+(\lambda P+\mu Q)'(0)=\lambda P(0)+\mu Q(0)+\lambda P'(0)+\mu Q'(0)=\lambda f(P)+\mu f(Q)\). Par contre, \(g\) ne l'est pas, puisque \(g(0)=1\neq 0\).
?Applications linéaires
Énoncé
On considère les applications suivantes : \(\begin{array}{rccc}f:&\mathbb{C}&\to&\mathbb{C}\\& z&\to& \Re (z)\end{array} \quad \mbox{et} \quad \begin{array}{rccc}g:&\mathbb{C}&\to&\mathbb{C}\\& z&\to& \Im (z), \end{array}\) où \(\Re (z)\) (resp. \(\Im (z)\)) est la partie réelle (resp. imaginaire) de \(z\). Quelles sont les assertions vraies ?
Correction
Explication Générale
On vérifie que \(f\) et \(g\) sont \(\mathbb{R}\)-linéaires car la partie réelle (resp. imaginaire) d'une somme est la somme des parties réelles (resp. imaginaires) et si \(\lambda\in\mathbb{R}\) et \(z\in\mathbb{C}\) alors \(\Re (\lambda z)=\lambda\Re(z)\) et \(\Im(\lambda z)=\lambda\Im(z)\). Par contre, elles ne sont pas \(\mathbb{C}\)-linéaires. Par exemple \(f(i\cdot i)=f(-1)=-1\neq 0=i\cdot f(i)\) et \(g(i\cdot 1)=g(i)=1\neq 0=i\cdot g(1)\).
?Applications linéaires
Énoncé
On considère les applications suivantes : \(\begin{array}{rccc}f:&\mathbb{C}&\to&\mathbb{C}\\& z&\to& |z|\end{array} \quad \mbox{et} \quad \begin{array}{rccc}g:&\mathbb{C}&\to&\mathbb{C}\\& z&\to& \overline{z},\end{array} \) où \(|z|\) (resp. \(\overline{z}\)) est le module (resp. le conjugué) de \(z\). Quelles sont les assertions vraies ?
Correction
Explication Générale
On vérifie que \(f\) n'est pas \(\mathbb{R}\)-linéaire (donc n'est pas \(\mathbb{C}\)-linéaire). En effet, le module d'une somme n'est pas en général la somme des modules comme le montre l'exemple \(|3+(-2)|=1\neq 5=|3|+|-2|\). En utilisant la définition d'application linéaire et les propriétés du conjugué on vérifie que \(g\) est \(\mathbb{R}\)-linéaire. Par contre, \(g\) n'est pas \(\mathbb{C}\)-linéaire comme le montre l'exemple \(g(i\cdot i)=-1\neq 1=i\cdot g(i)\).
?Fonction majorée/minorée (1)
Énoncé
Soit \(f : \mathbb{R} \to \mathbb{R}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Par définition \(f\) est majorée si \(\exists M > 0 \quad \forall x \in \mathbb{R} \quad f(x) \le M\).
Pour aller plus loin :
cours : Limites et fonctions continues
video : Fonctions bornées
?Fonctions - continuité sur R (1)
Énoncé
Parmi les fonctions suivantes, lesquelles sont continues sur \(\mathbf{R}\) ?
Correction
Explication Générale
La fonction tangente n'est pas définie partout, et elle continue seulement sur son domaine de définition. Comme \(\ln(\exp(3x)) = 3x\) alors cette fonction sera continue sur \(\mathbf{R}\).
Pour aller plus loin :
cours : Limites et fonctions continues
video : Continuité en un point
video : Notion sur les fonctions
video : La bijection
exercices : Fonctions continues
?Fonctions - continuité en un point (2)
Énoncé
Parmi les propriétés suivantes, quelles sont celles qui signifient que \(f\) est continue en \(x_ 0\) ?
Correction
Explication Générale
\(f\) est continue en \(x_0\) si \(\lim_{x\to x_0} f(x) = f(x_0)\), ce qui s'écrit aussi \(\big| f(x) - f(x_0) \big| \to 0\) lorsque \(x\) tend vers \(x_0\), ou encore : \((\forall \epsilon > 0 \quad \exists \delta > 0 \qquad |x-x_0| < \delta \implies |f(x)-f(x_0)| < \epsilon)\) (et on peut remplacer les inégalités strictes par des inégalités larges).
Attention écrire \(\exists \delta > 0\quad\forall \epsilon\) une propriété est vraie ne veut pas dire la même chose que : \(\forall \epsilon \quad \exists \delta > 0 \) telle que cette même propriété est vraie.
Pour aller plus loin :
cours : Limites et fonctions continues
video : Continuité en un point
video : Notion sur les fonctions
video : La bijection
exercices : Fonctions continues
?Fonctions - continuité sur R (2)
Énoncé
Parmi les fonctions suivantes, lesquelles sont continues sur \(\mathbb{R}\) ?
Correction
Explication Générale
La fonction \(f\) définie par \(f(x) = 0\), si \(x\in \mathbb{Q}\) et par \(f(x)=1\) sinon, est une fonction qui n'est continue en aucun point \(x_0\in \mathbb{R}\).
Pour aller plus loin :
cours : Limites et fonctions continues
video : Continuité en un point
video : Notion sur les fonctions
video : La bijection
exercices : Fonctions continues
?Fonctions - continuité sur R (3)
Énoncé
Pour toutes les fonctions notées f qui suivent on pose \(f(0)=0\). Quelles sont alors les fonctions f continues lorsque pour tout \(x\) réel et différent de 0 on pose :
Correction
Explication Générale
Toutes les fonctions sont continues sur \(\mathbb{R}^*\), il s'agit donc de déterminer si \(f(x) \to 0\) lorsque \(x\to0\). C'est uniquement le cas de \(x \ln( |x|)\).
Pour aller plus loin :
?Fonctions : maximum/minimum (1)
Énoncé
Soit \(f : [a,b] \to \mathbb{R}\) continue sur l'intervalle \([a,b]\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Une fonction continue sur un intervalle fermé borné, est bornée et atteint ses bornes (donc le maximum et le minimum sont atteints). Par contre ses extremums peuvent être en \(a\) ou en \(b\) ou dans \(]a,b[\).
Pour aller plus loin :
cours : Limites et fonctions continues
video : Continuité en un point
video : Extremum d'une fonction
exercices : Fonctions continues
?Fonctions réelles - dérivée en un point (2)
Énoncé
Soit \(\displaystyle f(x)=\sqrt[3]{(x-2)^2}\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
Les théorèmes généraux impliquent que \(f\) est continue sur \(\mathbf{R}\) et est dérivable sur \(\mathbf{R}\setminus\{2\}\). Mais \(\lim_{x\to 2^{\pm}}\frac{f(x)-f(2)}{x-2}=\lim_{x\to 2^{\pm}}\frac{1}{\sqrt[3]{x-2}}={\pm}\infty \) Donc, \(f\) n'est pas dérivable en \(2\) et la tangente à la courbe représentative de \(f\) au point d'abscisse \(2\) est une droite verticale.
?Fonctions réelles : calcul de dérivée (4)
Énoncé
Soit \(x\in\mathbb R\), soit \(\displaystyle f(x)=x^2-\mathrm{e}^{x^2-1}\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On calcule \(f'(x)=2x-2x\mathrm{e}^{x^2-1}\) et \(f''(x)=2-2(1+2x^2)\mathrm{e}^{x^2-1}\). Ensuite, on vérifie que \(f'(x)=0\mbox{ et }f''(0)=2-2\mathrm{e}^{-1} > 0.\) Donc \(f\) admet un minimum local en \(0\) et la tangente à la courbe représentative de \(f\) au point d'abscisse \(0\) est une droite horizontale.
Pour aller plus loin :
cours : Dérivée d'une fonction
video : Définition de la dérivée
video : Extremum local
?Fonctions réelles : calcul de dérivée (5)
Énoncé
Soit \(x\in\mathbb R\), soit \(\displaystyle f(x)=x^4-x^3+1\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On a \(f'\left(\frac{3}{4}\right)=0\) et \(f''\left(\frac{3}{4}\right) > 0\). Donc \(f\) admet un minimum au point \(\displaystyle \frac{3}{4}\). On vérifie aussi que \(f''\) et \(f''\) s'annulent en \(0\) en changeant de signe. Donc la courbe représentative de \(f\) admet un point d'inflexion au point d'abscisse \(0\).
Pour aller plus loin :
cours : Dérivée d'une fonction
video : Définition de la dérivée
video : Extremum local
?Dérivabilité des fonctions réelles - tangente (1)
Énoncé
Soit \(x\in\mathbb R\), soit \(\displaystyle f(x)=x^4-3x^3+3x^2-x\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
La fonction \(f\) est dérivable sur \(\mathbf{R}\). En particulier, la tangente à la courbe représentative de \(f\) en un point \(a\in \mathbf{R}\) ne peut être une droite verticale. Par ailleurs, \(f(0)=f(1)=0\). Donc le théorème de Rolle implique l'existence de \(a\in ]0,1[\) tel que \(f'(a)=0\) et la tangente à la courbe représentative de \(f\) en ce point est une droite horizontale.
Pour aller plus loin :
cours : Dérivée d'une fonction
video : Définition de la dérivée
video : Définition de la tangente
video : Calculs dérivées usuelles
video : Extremum local
video : Théorème de Rolle
exercices : Fonctions dérivables
?Dérivée seconde ou plus - maximum/minimum
Énoncé
Soit \(x\in\mathbb R\), soit \(\displaystyle f(x)=\mathrm{e}^{3x^4-4x^3}\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On a \(f'(x)=(12x^3-12x^2)\mathrm{e}^{3x^4-4x^3}=12x^2(x-1)\mathrm{e}^{3x^4-4x^3}\). On en déduit que \(f'(1)=0\) et \(f'(x) < 0\) pour \(x < 1\) et \(f'(x) > 0\) pour \(x > 1\). Donc \(f\) admet un minimum en \(1\). Par ailleurs, \(f'(0)=f'(1)=0\) et, puisque \(f'\) est continue sur \([0,1]\) et est dérivable sur \(]0,1[\), le théorème de Rolle implique qu'il existe \(a\in ]0,1[\) tel que \(f''(a)=0\).
Pour aller plus loin :
cours : Dérivée d'une fonction
video : Définition de la dérivée
video : Extremum local
video : Théorème de Rolle
exercices : Fonctions dérivables
?Développements limités
Énoncé
Parmi les égalités suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
On a : \(\displaystyle DL_1(0)\mathrm{e}^{x}-1=x+o(x)\) et \(\displaystyle DL_1(0)(\sqrt{1+x}-1)=\frac{x}{2}+o(x)\). Donc \(\displaystyle DL_0(0)\frac{\mathrm{e}^{x}-1}{\sqrt{1+x}-1}=2+o(1)\Rightarrow \displaystyle\lim _{x\to 0}\frac{\mathrm{e}^{x}-1}{\sqrt{1+x}-1}=2\). De même, \(\displaystyle DL_1(0)(\mathrm{e}^{x}-\sqrt{1+2x})=o(x)\) et \(\displaystyle DL_1(0)\ln(1+x)=x+o(x)\). Donc \(\displaystyle DL_0(0)\frac{\mathrm{e}^{x}-\sqrt{1+2x}}{\ln(1+x)}=o(1)\Rightarrow \lim _{x\to 0}\frac{\mathrm{e}^{x}-\sqrt{1+2x}}{\ln(1+x)}=0\). Ensuite, \(\displaystyle 1-\cos x=\frac{x^2}{2}+o(x^2)\) et \(\displaystyle \sin ^2x=x^2+o(x^2)\). D'où \(\displaystyle \frac{1-\cos x}{\sin ^2x}=\frac{1}{2}+o(1)\). On en déduit la limite en \(0\). Enfin, \(\mathrm{e}^x-\cos x-x=x^2+o(x^2)\Rightarrow \frac{\mathrm{e}^x-\cos x-x}{x^2}=1+o(1)\Rightarrow \lim _{x\to 0}\frac{\mathrm{e}^x-\cos x-x}{x^2}=1\).
?Développements limités
Énoncé
Soit \(\displaystyle f(x)=\frac{\ln x}{x^2-1}\) et \(\displaystyle g(x)=\frac{\ln (1+x)}{2x+x^2}\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Les développements à l'ordre \(2\) en \(0\) de \(\ln (1+x)\) donne : \(\displaystyle DL_1(0)g(x)=\frac{1}{2}-\frac{x}{2}+o(x) \Rightarrow DL_1(1)f(x)=\frac{1}{2}-\frac{x-1}{2}+o(x-1)\) car \(f(x)=g(x-1)\). Enfin, \(\displaystyle \lim _{x\to 1}f(x)=\lim _{x\to 0}g(x)=\frac{1}{2}\).
?Développements limités
Énoncé
Soit \(\displaystyle f(x)=\frac{x^2}{x^2+2x+2}\) et \(g(x)=f(x-1)\). On note \(T\) la tangente au graphe de \(f\) au point d'abscisse \(-1\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
D'abord \(\displaystyle g(x)=\frac{1-2x+x^2}{1+x^2}=1-2x+2x^3+o(x^3)\). On en déduit que \(\displaystyle DL_3(-1)f(x)=1-2(x+1)+2(x+1)^3+o\left((x+1)^3\right)\). Donc \(T\) est la droite d'équation \(y=1-2(x+1)\) et le point d'abscisse \(-1\) est un point d'inflexion.
?Développements limités
Énoncé
Soit \(\displaystyle f(x)=x-\sin x\). On note \(T_0\) la tangente au graphe de \(f\) au point d'abscisse \(0\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Le \(DL_3(0)\sin x\) donne \(\displaystyle DL_3(0)f(x)=\frac{x^3}{6}+o(x^3)\). Donc \(T_0\) est la droite d'équation \(y=0\). Or, au voisinage de \(0\), on a : \(f(x)-y=\frac{x^3}{6}+o(x^3)\). Ce qui implique que le point d'abscisse \(0\) est un point d'inflexion. Enfin, \(\displaystyle \lim _{x\to 0}\frac{f(x)}{x^2}=\lim _{x\to 0}\left(\frac{x}{6}+o(x)\right)=0\).
?Développements limités
Énoncé
Soit \(\displaystyle f(x)=x^2\ln \left(\frac{x+1}{x}\right)\). On note \(\Gamma\) le graphe de \(f\) et on pose \(\displaystyle g(x)=xf\left(\frac{1}{x}\right)\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
D'abord, \(\displaystyle g(x)=\frac{\ln (1+x)}{x}=1-\frac{x}{2}+\frac{x^2}{3}+o(x^2)\). Donc, au voisinage de \(\pm\infty\), on a : \(f(x)=x-\frac{1}{2}+\frac{1}{3x}+o\left(\frac{1}{x}\right)\mbox{ car }f(x)=xg\left(\frac{1}{x}\right)\). La droite d'équation \(\displaystyle y=x-\frac{1}{2}\) est une asymptote au voisinage de \(\pm\infty\). De plus, au voisinage de \(-\infty\), \(\displaystyle f(x)-y=\frac{1}{3x}+o\left(\frac{1}{x}\right)\leq 0\). Donc \(\Gamma\) est en dessous de cette droite au voisinage de \(-\infty\).
?Développements limités
Énoncé
Parmi les égalités suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
On a : \(\displaystyle \left(1+x\right)^{1/x}=\mathrm{e}^{\frac{\ln (1+x)}{x}}\) et \(\displaystyle \frac{\ln (1+x)}{x}=1+o(1)\). Donc \(\mathrm{e}^{\frac{\ln (1+x)}{x}}=\mathrm{e}+o(1) \Rightarrow \lim _{x\to 0}\left(1+x\right)^{1/x}=\mathrm{e}\). De même, \(\displaystyle \left(\cos x\right)^{1/\sin ^2x}=\mathrm{e}^{\ln (\cos x)/\sin ^2x}\). Or \(\sin ^2x=x^2+o(x^2)\) et \(\displaystyle \ln (\cos x)=\ln \left(1-\frac{x^2}{2}+o(x^2)\right)=-\frac{x^2}{2}+o(x^2)\). Donc \(\frac{\ln (\cos x)}{\sin ^2x}=-\frac{1}{2}+o(1)\Rightarrow \lim _{x\to 0}\left(\cos x\right)^{1/\sin ^2x}=\mathrm{e}^{-1/2}\). Ensuite, \(\displaystyle \frac{1}{\sin ^2x}-\frac{1}{x^2}=\frac{x^2-\sin ^2x}{x^2\sin ^2x}\), et le \(\displaystyle DL_4(0)\sin ^2x=x^2-\frac{x^4}{3}+o(x^4)\) donne \(DL_0(0)\frac{x^2-\sin ^2x}{x^2\sin ^2x}=\frac{1}{3}+o(1)\Rightarrow \lim _{x\to 0}\left(\frac{1}{\sin ^2x}-\frac{1}{x^2}\right)=\frac{1}{3}\). Enfin, \(\displaystyle \cos x=1-\frac{x^2}{2}+\frac{x^4}{24}+o(x^4)\), \(\displaystyle \sqrt{1-x^2}=1-\frac{x^2}{2}-\frac{x^4}{8}+o(x^4)\) et \(x^2\sin ^2x=x^4+o(x^4)\). Donc \(\frac{\cos x-\sqrt{1-x^2}}{x^2\sin ^2x}=\frac{x^4/6+o(x^4)}{x^4+o(x^4)}=\frac{1}{6}+o(1)\Rightarrow \lim _{x\to 0}\frac{\cos x-\sqrt{1-x^2}}{x^2\sin ^2x}=\frac{1}{6}\).
?Équations différentielles du premier ordre
Énoncé
On considère les équations différentielles : \((E_1)\; :\; y'-2y=0\quad \mbox{ et }\quad (E_2)\; :\; y'+2xy=0\).
Parmi les affirmations suivantes cocher celles qui sont vraies :
Correction
Explication Générale
Une primitive de \(-2\) est \(-2x\), donc la solution générale de \((E_1)\) sur \(\mathbb{R}\) est : \(y=k\mathrm{e}^{2x},\quad k\in \mathbb{R}\). Une primitive de \(2x\) est \(x^2\), donc la solution générale de \((E_2)\) sur \(\mathbb{R}\) est : \(y=k\mathrm{e}^{-x^2},\quad k\in \mathbb{R}\).
?Équations différentielles du premier ordre
Énoncé
On considère les équations différentielles : \((E_1)\; :\; (1+x^2)y'-y=0\quad\mbox{et}\quad (E_2)\; :\; y'-\frac{y}{1+x^2}=0\).
Parmi les affirmations suivantes cocher celles qui sont vraies :
Correction
Explication Générale
En divisant \((E_1)\) par \(1+x^2\), on obtient \((E_2)\) : \((E_1)\) et \((E_2)\) ont les mêmes solutions. Une primitive de \(\displaystyle \frac{-1}{1+x^2}\) est \(-\arctan x\), donc la solution générale de \((E_1)\) sur \(\mathbb{R}\) est : \(y=k\mathrm{e}^{arctan (x)}\), \(k\in \mathbb{R}\).
?Équations différentielles du second ordre
Énoncé
On considère les équations différentielles : \((E_1)\; :\; y''-4y=4x\quad \mbox{et}\quad (E_2)\; :\; y''+2y'+y=x+2\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Les solutions de l'équation caractéristique associée à \((E_1)\) sont \(\pm 2\) et \(y_0=-x\) est une solution particulière de \((E_1)\). Donc la solution générale de \((E_1)\) est : \(y=-x+k_1\mathrm{e}^{2x}+k_2\mathrm{e}^{-2x},\quad k_1,k_2\in \mathbb{R}\). L'équation caractéristique associée à \((E_2)\) admet \(-1\) comme racine double et \(y_0=x\) est une solution particulière de \((E_2)\). Donc la solution générale de \((E_2)\) est : \(y=x+(k_1x+k_2)\mathrm{e}^{-x},\quad k_1,k_2\in \mathbb{R}.\)
?Équations différentielles du second ordre
Énoncé
Sur \(\mathbb{R}\), on considère les équations différentielles : \((E_1)\; :\; y''-y'-2y=2\quad \mbox{et}\quad (E_2)\; :\; y''+y=x\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Les solutions de l'équation caractéristique associée à \((E_1)\) sont \(2\) et \(-1\) et \(y_0=-1\) est une solution particulière de \((E_1)\). Donc la solution générale de \((E_1)\) est \(y=-1+k_1\mathrm{e}^{2x}+k_2\mathrm{e}^{-x},\quad k_1,k_2\in \mathbb{R}.\) Les solutions de l'équation caractéristique associée à \((E_2)\) sont \(\pm \mathrm{i}\) et \(y_0=x\) est une solution particulière de \((E_2)\). Donc la solution générale de \((E_2)\) est \(y=x+k_1\cos (x)+k_2\sin (x),\quad k_1,k_2\in \mathbb{R}\).
?Intégration par parties
Énoncé
On note par \(F\) une primitive de \(f(x)=\ln x\) sur \(]0,+\infty[\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Une intégration par parties avec \(u=\ln x\) et \(v=x\) donne \(\int \ln x\mathrm{d}x=x\ln x-\int \mathrm{d}x=x\ln x-x+k,\; k\in \mathbb{R}\).
?Intégration par parties
Énoncé
On note par \(F\) une primitive de \(f(x)=x\ln x\) sur \(]0,+\infty[\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Une intégration par parties, avec \(u=\ln x\) et \(v=x^2/2\), donne \(F(x)=\frac{x^2}{2}\ln x-\frac{1}{2}\int x\mathrm{d}x=\frac{x^2}{2}\ln x-\frac{x^2}{4}+k,\; k\in \mathbb{R}\).
?Intégration par parties
Énoncé
On note par \(F\) une primitive de \(f(x)=x\mathrm{e}^x\) sur \(\mathbb{R}\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Une intégration par parties avec \(u=x\) et \(v=\mathrm{e}^x\) donne \(F(x)=x\mathrm{e}^x-\int \mathrm{e}^x\mathrm{d}x=x\mathrm{e}^x-\mathrm{e}^x+k,\mbox{ où }k\in \mathbb{R}\).
?Intégrale définie
Énoncé
L'intégrale \(\displaystyle \int _{-\pi/6}^{\pi/3}\tan x\, \mathrm{d}x\) est égale à :
Correction
Explication Générale
La relation de Chasles donne \(\displaystyle \int _{-\pi/6}^{\pi/3}\tan x\, \mathrm{d}x=\int _{-\pi/6}^{\pi/6}\tan x\, \mathrm{d}x+\int _{\pi/6}^{\pi/3}\tan x\, \mathrm{d}x\) et \(\displaystyle \int _{-\pi/6}^{\pi/6}\tan x\, \mathrm{d}x=0\) car \(\tan \) est impaire. Ensuite, on écrit \(\displaystyle \tan x=\frac{\sin x}{\cos x}\) et on pose \(t=\cos x\Rightarrow \mathrm{d}t=-\sin x\, \mathrm{d}x\). D'où, \(\displaystyle \int _{\pi/6}^{\pi/3}\tan x\, \mathrm{d}x=-\int _{\sqrt{3}/2}^{1/2}\frac{\mathrm{d}t}{t}=\ln \sqrt{3}\).
?Limites des fonctions réelles - limite en un point d'une fraction rationnelle (1)
Énoncé
Soit \(f(x)= \frac{x^2-1}{2x^2-x-1}\). Quelles sont les assertions (ou proposition) vraies ?
Correction
Explication Générale
\(f(x)=\frac{(x-1)(x+1)}{(x-1)(2x+1)}= \frac{x+1}{2x+1}\). On cherche à mettre en facteur \((x-1) \) au numérateur et au dénominateur puisqu'ils s'annulent tous les deux en \(1\).
Pour aller plus loin :
exercices : Limites de fonctions
?Limites des fonctions réelles - limite en un point d'une fraction rationnelle (2)
Énoncé
Soit \(f(x)= \frac{1}{x+1}+ \frac{3x}{(x+1)(x^2-x+1)}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
En réduisant au même dénominateur, on obtient : \(f(x)= \frac{x+1}{x^2-x+1}\). Et la limite en l'infini d'une fraction rationnelle est la limite de la fraction de ses monômes de plus haut degré.
exercices : Limites de fonctions
?Limites des fonctions réelles - limite en l'infini (1)
Énoncé
Soit \(f(x)= \sqrt{x^2+x+1}+x\). Quelles sont les assertions vraies ?
Correction
Explication Générale
On multiplie le numérateur et le dénominateur de \(f\) par l'expression conjuguée de \(\sqrt{x^2+x+1}+x\), c'est-à-dire par \(\sqrt{x^2+x+1}-x\). On obtient : \(f(x)= \frac{x+1}{\sqrt {x^2+x+1}-x}\). Attention ! \(\sqrt {x^2+x+1}=|x|\sqrt {1+\frac{1}{x}+ \frac{1}{x^2}}= -x\sqrt {1+\frac{1}{x}+ \frac{1}{x^2}}, \) pour \(x < 0\).
Pour aller plus loin :
exercices : Limites de fonctions
?Limites des fonctions réelles - limite en l'infini (3)
Énoncé
Soit \(f(x)= (x^5-x^3+1)e^{-x}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Si \(\alpha\) et \( \beta\) sont des réels \( > 0\), alors en \(+\infty\), on a : \( x^{\alpha}\ll e^{\beta x}\), où la notation \(f\ll g\) signifie : \(\lim_{x \to + \infty} \frac{f(x)}{g(x)}=0 \).
Pour aller plus loin :
video : Exponentielle
?Limites des fonctions réelles - fonctions trigonométriques
Énoncé
Soit \(f(x)= \sin x \cdot \sin\frac{1}{x}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Encadrer \(\sin\frac{1}{x}\) pour la limite en \(0\) et encadrer \(\sin x\) pour la limite en \(+\infty\).
Pour aller plus loin :
video : Opérations sur les limites
exercices : Limites de fonctions
?Limites des fonctions réelles - limite en l'infini (4)
Énoncé
Soit \(f(x)= e^{-x}\cos(e^{2x})\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Encadrer \(\cos(e^{2x})\) pour la limite en \(+\infty\).
Pour aller plus loin :
video : Opérations sur les limites
exercices : Limites de fonctions
?Limites des fonctions réelles - limite en un point
Énoncé
Soit \(f(x)= \frac{\ln(1+x)}{x}\). Quelles sont les assertions (ou propositions) vraies ?
Correction
Explication Générale
La fonction \(g: x\to \ln(1+x)\) est dérivable sur \(]-1,+\infty[\) et \(g'(x)= \frac{1}{1+x}\), pour tout \(x > -1\). Donc \(\lim_{x\to 0}f(x)= \lim_{x\to 0}\frac{g(x)-g(0)}{x-0} = g'(0)=1\).
Pour aller plus loin :
video : Logarithme Népérien
?Limites des fonctions réelles - limite en un point
Énoncé
Soit \(f(x)= \frac{\sin x}{x}\). Quelles sont les assertions (ou propositions) vraies ?
Correction
Explication Générale
La fonction \(g: x\to \sin x\) est dérivable sur \(\mathbf{R}\) et \(g'(x)= \cos x\), pour tout \(x\in \mathbf{R}\). Donc \(\lim_{x\to 0}f(x)= \lim_{x\to 0}\frac{g(x)-g(0)}{x-0} = g'(0)=1\).
Pour aller plus loin :
video : La fonction sinus
?Nombres complexes - module/argument
Énoncé
Soit \(z=\frac{\cos \theta + i \sin \theta}{\cos \phi - i \sin \phi}\), \(\theta, \phi \in \mathbf{R}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Utiliser l'écrire trigonométrique et la formule : \(\frac{e^{i\theta}}{e^{-i\phi}}= e^{i(\theta + \phi)} \).
Pour aller plus loin :
video : Module d'un nombre complexe
video : Argument d'un nombre complexe
?Nombres complexes - module/argument
Énoncé
Soit \(E\) l'ensemble des points \(M\) d'affixe \(z\) tels que : \(|\frac{z-1}{1+iz}|=\sqrt 2\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Soit \(z \neq i\). On a :\(|\frac{z-1}{1+iz}|=\sqrt 2 \Leftrightarrow |z-1|^2=2|1+iz|^2 \Leftrightarrow (z-1)(\overline{z}-1)=2(1+iz)(1-i\overline{z})\). On développe cette dernière égalité.
Pour aller plus loin :
video : Nombres complexes et géométrie
exercices : Nombres complexes
?Suites réelles - limite
Énoncé
Soit \(n\) un entier naturel et soit \(\displaystyle u_n=\frac{\cos n}{2n+1}\) et \(\displaystyle v_n=\frac{2n+\cos n}{2n+1}\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On utilise le théorème d'encadrement, \(\displaystyle 0\leq \left|\frac{\cos n}{2n+1}\right|\leq \frac{1}{2n+1}\underset{+\infty}{\longrightarrow }0\). Donc \(\displaystyle \lim _{n\to +\infty}u_n=0\) et, puisque \(\displaystyle v_n=\frac{2n}{2n+1}+u_n\), \(\displaystyle \lim _{n\to +\infty}v_n=\lim _{n\to +\infty}\frac{2n}{2n+1}+\lim _{n\to +\infty}u_n=1\).
Pour aller plus loin :
?Congruences
Énoncé
Soient \(a_1,a_2, b_1, b_2\) et \(c_1,c_2\) des entiers.
On suppose que l'on a les congruences \(a_1\equiv b_1 \,[c_1]\) et \(a_2\equiv b_2 \,[c_2]\).
Que peut-on en déduire ?
Correction
Explication Générale
Par exemple, on a : \(2 \equiv 0 \; [2]\), et \(6 \equiv0 \; [3]\), cependant on ne trouve pas : \(8 \equiv 0 \; [5]\).
De même, on a : \(3\equiv 1 \; [2]\), et \(5 \equiv 1 \; [4]\), mais on n'a pas : \(15\equiv 1 \; [8]\).
?Congruences
Énoncé
Soient \(a_1,a_2, b_1, b_2\) et \(d\) des entiers.
On suppose que l'on a les congruences \(a_1\equiv b_1 \,[d]\) et \(a_2\equiv b_2 \,[d]\).
Que peut-on en déduire ?
Correction
Explication Générale
Pour la somme et le produit, ce sont des propriétés des congruences.
Pour aller plus loin voir (dans la partie "congruence") : http://ressources.unisciel.fr/sillages/mathematiques/algebre_revisions/08_Arithmetique/co/06_Congruence.html
?Dérivée d'une fonction composée
Énoncé
Quel est la fonction dérivée de la fonction suivante :
\(\begin{array}{rcl}\mathbb{R} & \rightarrow & \mathbb{R} \\x & \mapsto & \cos(x^{2}+2x+3)\end{array}\)
Correction
Explication Générale
La fonction s'écrit comme composée des fonction cosinus et de la fonction \(x \mapsto x^{2}+2x+3\). Il s'agit alors d'utiliser le théorème de dérivation d'une fonction composée. Plus précisément, on a \((f(U))'=U' \cdot f'(U)\), avec \(U=x^{2}+2x+3\) et \(f(x)=\cos(x)\). On sait que \(f'(x)=-\sin(x)\), et on a \(U'=2x+2=2(x+1)\). D'où, \((\cos(x^{2}+2x+3))'=-2(x+1)\sin(x^2+2x+3)\).
?Dérivée d'une fonction composée
Énoncé
Soit \(f: \mathbb{R} \rightarrow \mathbb{R}\) une fonction dérivable sur \(\mathbb{R}\). On note
\(\begin{array}{rrcl}g: & \mathbb{R} & \rightarrow & \mathbb{R} \\& x & \mapsto & f(x^{2}+1)\end{array}\)
Pour \(x \in \mathbb{R}\), que vaut \(g'(x)\) ?
Correction
Explication Générale
La fonction \(g\) est la composée de la fonction \(f\) avec la fonction \(x \mapsto x^{2}+1\), dérivable sur \(\mathbb{R}\). Il s'agit alors d'appliquer le théorème de dérivation des fonctions composées. Plus précisément, on a \(g'=(f(U))'=U' \cdot f'(U)\) avec \(U=x^2+1\).
On a \(U'=2x\). D'où, \(g'(x)=2x \cdot f'(x^2+1)\).
?Dérivée d'une fonction composée
Énoncé
Soit \(f: \mathbb{R} \rightarrow \mathbb{R}\) une fonction dérivable sur \(\mathbb{R}\). On note
\(\begin{array}{rrcl}g: & \mathbb{R} & \rightarrow & \mathbb{R} \\& x & \mapsto & \sin(f(x))\end{array}\)
Pour \(x \in \mathbb{R}\), que vaut \(g'(x)\) ?
Correction
Explication Générale
La fonction \(g\) est la composée de la fonction sinus avec la fonction \(f\). Il s'agit alors d'appliquer le théorème de dérivation des fonctions composées.
Plus précisément, on a \(g'=(h(U))'=U' \cdot h'(U)\) avec \(U=f(x)\) et \(h(x)=\sin(x)\). On a \(h'(x)=\cos(x)\) et \(U'=f'(x)\). Donc \(g'(x)=f'(x)\cos(f(x))\).
?Dérivée d'une fonction composée
Énoncé
Sur quel ensemble la fonction \(f\) définie par l'expression
\(f(x)= \sqrt{x^{2}-1}\)
est-elle dérivable ?
Correction
Explication Générale
La fonction \(f\) est définie sur l'ensemble des points \(x\) qui vérifient \(x^2-1 \geq 0 \Leftrightarrow x^2 \geq 1 \Leftrightarrow |x| \geq 1\). Donc \(f\) est définie sur \(]-\infty,-1] \cup [1,+\infty[ \). Puis on a \(f'(x)=\frac{2x}{2 \cdot \sqrt{x^2-1}}=\frac{x}{\sqrt{x^2-1}}\) pour tout \(x\) tel que \(x^2-1>0\) \(\Leftrightarrow |x|>1\). Autrement dit, \(f\) est dérivable sur \(]-\infty,-1[ \cup ]1,+\infty[ \).
?Dérivée d'une fonction composée
Énoncé
Soit \(f\) la fonction définie par l'expression :
\(f(x)= \sqrt{x^{2}-1}\).
On fixe un réel \(x\). Que vaut \(f'(x)\) dans le cas où cette quantité existe ?
Correction
Explication Générale
La fonction \(f\) est la composée de la fonction racine carrée avec la fonction \(x \mapsto x^{2}-1\). Il s'agit alors d'appliquer le théorème de dérivation des fonctions composées. Plus précisément, \(f'=(g(U))'=U' \cdot g'(U)\), avec \(U=x^2-1\) et \(g(x)=\sqrt{x}\).
On a \(U'=2x\) et \(g'(x)=\frac{1}{2\sqrt{x}}\). D'où, \( f'(x)=2x \cdot \frac{1}{2\sqrt{x^2-1}} = \frac{x}{\sqrt{x^2-1}}\).
?Équations différentielles
Énoncé
Les solutions de \(y'' +2y' +y=0\) sont les fonctions définies par :
Correction
Explication Générale
L'équation caractéristique associée à l'équation \(y'' +2y' +y=0\) est : \(r^2+2r+1=0=(r+1)^2\) qui a pour racine double \(r=-1\). On sait alors que les solutions sont les fonctions \(y(x)=(A+Bx )e^{-x}\) où \(A\) et \(B\) \(\in \mathbb{R}\).
Pour revoir les théorèmes sur les équations différentielles linéaires d'ordre 2 à coefficients constants :
?Équations différentielles
Énoncé
Les solutions de \(y'' -y' -2y=0\) sont les fonctions définies par :
Correction
Explication Générale
L'équation caractéristique associée à l'équation \(y''-y'-2y=0\) est \(r^2-r-2=0\) qui admet deux racines distinctes réelles \(r_1=-1\) et \(r_2=2\). On sait alors que les solutions sont les fonctions \(y(x)=Ae^{-x}+Be^{2x}\) où \(A\) et \(B\) \(\in \mathbb{R}\).
Pour revoir les théorèmes sur les équations différentielles linéaires d'ordre 2 à coefficients constants :
?Équations différentielles
Énoncé
Les solutions de \(y'' -y' -2y=0\) qui vérifient les conditions initiales \(y(0)=0\) et \(y' (0)=0\) sont :
Correction
Explication Générale
L'équation caractéristique associée à l'équation \(y''-y'-2y=0\) est \(r^2-r-2=0\) qui admet deux racines distinctes réelles \(r_1=-1\) et \(r_2=2\). On sait alors que les solutions de \(y''-y'-2y=0\) sont les fonctions \(y(x)=Ae^{-x}+Be^{2x}\) où \(A\) et \(B\) \(\in \mathbb{R}\). Avec les conditions initiales \(y(0)=0\) et \(y'(0)=0\), on a :
\(\begin{cases}A+B=0 \\-A+2B=0\end{cases}\)
D'où, \( A=B=0\). Donc \(y=0\).
Pour revoir les théorèmes sur les équations différentielles linéaires d'ordre 2 à coefficients constants :
?Équations différentielles
Énoncé
Les solutions de \(y'' -y' -2y=0\) qui vérifient les conditions initiales \(y(0)=0\) et \(y' (0)=3\) sont :
Correction
Explication Générale
L'équation caractéristique associée à l'équation \(y''-y'-2y=0\) est \(r^2-r-2=0\) qui admet deux racines distinctes réelles \(r_1=-1\) et \(r_2=2\). On sait alors que les solutions de \(y''-y'-2y=0\) sont les fonctions \(y(x)=Ae^{-x}+Be^{2x}\) où \(A\) et \(B\) \(\in \mathbb{R}\). Avec les conditions initiales \(y(0)=0\) et \(y'(0)=3\), on a :
\(\begin{cases}A+B=0 \\-A+2B=3 \end{cases}\) \(\Longleftrightarrow\) \(\begin{cases}A=-B \\ 3B=3 \end{cases}\)
Donc, \(B=1\), et \(A=-1\). L'unique solution est donc \(y(x)=-e^{-x}+e^{2x}\).
Pour revoir les théorèmes sur les équations différentielles linéaires d'ordre 2 à coefficients constants :
?Limite d'une fonction
Énoncé
Soit \(\varphi\) la fonction définie sur \(\mathbb{R}^*\) par \(\varphi(x)=\exp\left(\frac{1}{x^2}\right)\).
Laquelle des proposition suivantes est vraie ?
Correction
Explication Générale
\(\displaystyle\lim_{x\to -\infty}\frac{1}{x^2}=0\) et \(\displaystyle\lim_{x\to 0}\exp(x)=\exp(0)=1\) donc \(\displaystyle\lim_{x\to -\infty}\exp\left(\frac{1}{x^2}\right)=1\).
?Limite d'une fonction
Énoncé
\(\displaystyle \lim_{x \rightarrow +\infty} \frac{x^3+x+1}{x+ \sqrt{x}+1}\) vaut :
Correction
Explication Générale
On a \(\frac{x^3+x+1}{x+ \sqrt{x}+1} = \frac{x^3 \cdot (1+\frac{x}{x^3}+\frac{1}{x^3})}{x \cdot (1+ \frac{\sqrt{x}}{x}+\frac{1}{x})}=\)\(\frac{x^2 \cdot (1+\frac{1}{x^2}+\frac{1}{x^3})}{1+ \frac{1}{\sqrt{x}}+\frac{1}{x}}\). Or, \(\displaystyle \lim_{x \rightarrow +\infty} 1+ \frac{1}{\sqrt{x}}+\frac{1}{x}=1\) et \(\displaystyle \lim_{x \rightarrow +\infty} 1+\frac{1}{x^2}+\frac{1}{x^3} = 1\). Et \(\displaystyle \lim_{x \rightarrow +\infty} x^2 = +\infty\). D'où, \(\displaystyle \lim_{x \rightarrow +\infty} \frac{x^3+x+1}{x+ \sqrt{x}+1}= + \infty\).
?Limite d'une fonction
Énoncé
\(\displaystyle \lim_{x \rightarrow -\infty} \frac{e^{x}+x}{e^{x}+1}\) vaut :
Correction
Explication Générale
On a \(\frac{e^{x}+x}{e^{x}+1} = \frac{x\cdot(\frac{e^{x}}{x}+1)}{e^{x}+1}\).
On sait que \(\displaystyle \lim_{x \rightarrow -\infty} e^x = 0\) et \(\displaystyle \lim_{x \rightarrow -\infty} \frac{e^{x}}{x} = \displaystyle \lim_{x \rightarrow -\infty} x^{-1} \cdot e^x=0\) (puisque l'exponentielle l'emporte sur les fonctions puissances en \(\pm \infty\)). Donc, \(\displaystyle \lim_{x \rightarrow -\infty} \frac{e^{x}}{x}+1=1\) et \( \displaystyle \lim_{x \rightarrow -\infty} e^{x}+1 = 1\). De plus, \(\displaystyle \lim_{x \rightarrow -\infty} x = - \infty\).
Donc, \(\displaystyle \lim_{x \rightarrow -\infty} \frac{e^{x}+x}{e^{x}+1} = - \infty\).
?Limite d'une fonction
Énoncé
\(\displaystyle \lim_{x \rightarrow +\infty} \frac{x+\ln(x)}{-x+\ln(x)}\) vaut :
Correction
Explication Générale
On a \(\frac{x+\ln(x)}{-x+\ln(x)}= \frac{x \cdot (1+\frac{\ln(x)}{x})}{ x \cdot (-1+\frac{\ln(x)}{x})}= \frac{1+\frac{\ln(x)}{x}}{ -1+\frac{\ln(x)}{x}}\).
Or, par croissances comparées on sait que \(\displaystyle \lim_{x \rightarrow +\infty} \frac{\ln(x)}{x} = 0\).
D'où, \( \displaystyle \lim_{x \rightarrow +\infty} \frac{x+\ln(x)}{-x+\ln(x)}=-1\).
?Limite d'une fonction
Énoncé
\(\displaystyle \lim_{x \rightarrow +\infty} e^{\ln(x)^2}\) vaut :
Correction
Explication Générale
On sait que \(\displaystyle \lim_{x \rightarrow +\infty} \ln(x) = +\infty\). Et donc \(\displaystyle \lim_{x \rightarrow +\infty} \ln(x)^2 = +\infty\).
On sait aussi que \( \displaystyle \lim_{x \rightarrow +\infty} e^x = +\infty\). Donc, d'après le théorème de composition des limites on a \(\displaystyle \lim_{x \rightarrow +\infty} e^{\ln(x)^2}= +\infty\).
?Limite d'une fonction
Énoncé
\(\displaystyle \lim_{x \rightarrow +\infty} \ln(\sqrt{\frac{x^2+3x+1}{x^{4}+x^2 +10}})\) vaut :
Correction
Explication Générale
D'abord on a : \(\sqrt{\frac{x^2+3x+1}{x^{4}+x^2 +10}} =\sqrt{\frac{x^2 \cdot (1+\frac{3x}{x^2}+\frac{1}{x^2})}{x^{4} \cdot (1+\frac{x^2}{x^4} +\frac{10}{x^4})}}=\sqrt{\frac{1+\frac{3}{x}+\frac{1}{x^2}}{x^2(1+\frac{1}{x^2} +\frac{10}{x^4})}}\).
Puis, on a \(\displaystyle \lim_{x \rightarrow +\infty} 1+\frac{3}{x}+\frac{1}{x^2} = 1\), et \(\displaystyle \lim_{x \rightarrow +\infty} 1+\frac{1}{x^2} +\frac{10}{x^4}=1\). Donc, \(\displaystyle \lim_{x \rightarrow +\infty} \sqrt{\frac{1+\frac{3}{x}+\frac{1}{x^2}}{x^2(1+\frac{1}{x^2} +\frac{10}{x^4})}}=0\).
Or, on sait que \(\displaystyle \lim_{x \rightarrow 0} \ln(x) = - \infty\).
Donc d'après le théorème de composition des limites, on obtient : \(\displaystyle \lim_{x \rightarrow +\infty} \ln(\sqrt{\frac{x^2+3x+1}{x^{4}+x^2 +10}}) = - \infty\).
?Limite d'une fonction
Énoncé
Soit \(f: \mathbb R\to \mathbb R\) la fonction définie par \(f(x)=\frac{(2e^x)x^2+1}{x^2+3}\).
Que penser de l'affirmation suivante : \(\lim_{x\to +\infty} f(x)= 2e^x\).
Correction
Explication Générale
L'affirmation n'a aucun sens : la valeur de la limite ne peut pas dépendre de la variable selon laquelle on prend la limite (\(x\) ici).
?Limite d'une fonction
Énoncé
Soit \(f: \mathbb R\to \mathbb R\) la fonction définie par \(f(x)=\frac{x^4+x+1}{4x^4+5}\).
Que penser de l'affirmation suivante : \(\lim\limits_{x\to +\infty} f(x)= \frac 1 4\).
Correction
Explication Générale
Pour tout \(x\in \mathbb R\), on a \(f(x)=\frac {x^4(1+\frac 1 {x^3} + \frac 1 {x^4})}{x^4(4 + \frac 5{x^4})}=\frac {1+\frac 1 {x^3} + \frac 1 {x^4}}{4 + \frac 5 {x^4}}\).
Comme \(\frac 1 {x^n} \xrightarrow[x \to+ \infty]{} 0\), pour \(n=3,4\), on a bien \(\lim\limits_{x\to +\infty} f(x)= \frac 1 4\).
?Limite d'une fonction
Énoncé
Soit \(f:\mathbb R \to \mathbb R\) une fonction ayant pour graphe :
Quelle est la valeur \(\lim\limits_{x\to 3^-}f(x)\) ?
Correction
Explication Générale
\(\lim\limits_{x\to 3^-}f(x)\) ne tient compte que des valeurs de \(f(x)\) pour \(x<3\).
?Limite d'une suite
Énoncé
La limite de la suite \(\displaystyle (u_n)_{n \in \mathbb N^*}\) de terme général \(\displaystyle u_n = \frac{\cos n}{n^2}\) est :
Correction
Explication Générale
Pour tout \(n\) dans \({\mathbb N}^*\), \(\displaystyle -1\leq \cos n \leq 1\), donc : \(\displaystyle -\frac1{n^2} \leq u_n \leq\frac1{n^2}\). Comme, \(\displaystyle \lim_{n \to +\infty}{\frac1{n^2}} = -\lim_{n\to +\infty}{\frac1{n^2}} = 0\), on obtient \(\displaystyle \lim_{n \to+\infty}{u_n} = 0\), par le théorème des gendarmes.
?Limite d'une suite
Énoncé
Soient \(\displaystyle (u_n)_{n \in \mathbb N}\) et \(\displaystyle(v_n)_{n \in \mathbb N}\) deux suites telles que : \(\forall n \in\mathbb N, \; 0 \leq v_n,\) et \(\forall n \in \mathbb N, \; \lvert u_n\rvert \leq v_n\). On suppose que la suite \(\displaystyle (v_n)_{n \in \mathbb N}\) est convergente. Parmi les propositions suivantes, lesquelles sont correctes ?
Correction
Explication Générale
Comme \((v_n)\) est convergente, elle est bornée et donc \((u_n)\) aussi \(\emph {a fortiori}\).
?Suites monotones
Énoncé
Soit la suite \(\displaystyle (u_n)_{n \in \mathbb N^*}\) de terme général \(\displaystyle u_n = 1 - \frac1{n^2}.\) Parmi les propositions suivantes, lesquelles sont correctes ?
Correction
Explication Générale
Comme \(\frac1{n^2} > \frac1{(n+1)^2}\), il est clair que la suite \(\displaystyle (u_n)_{n \in \mathbb N^*}\) est croissante. Pour tout \(n \in \mathbb N^*\), on a \(u_n < 1\) et donc \(2\) est un majorant. L'affirmation 3 suit du théorème de la limite monotone. On trouve que la limite est \(1\).
?Limite d'une suite
Énoncé
Quelle est la limite de la suite définie, pour tout entier \(n\geq 2\), par la terme \(\displaystyle \ a_n=\frac{2n^3-\ln n}{n-n^3}\) ?
Correction
Explication Générale
Le numérateur équivaut à \(2n^3\) car \(\ln n\) est négligeable devant \(2n^3\) par croissance comparée et le dénominateur équivaut à \(-n^3\). Le quotient équivaut alors à \(-2\), la suite a donc pour limite \(-2\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Sans faire de calcul, quel produit scalaire a la valeur la plus élevée ?
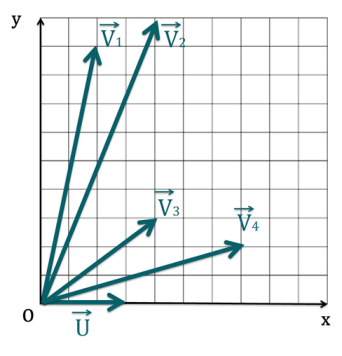
Correction
Explication Générale
Tous les produits scalaires sont calculés avec \(\overrightarrow{U}\) qui est parallèle à l'axe des \(x\).
Pour déterminer le produit scalaire le plus élevé on compare les composantes selon \(x\) des vecteurs \(\overrightarrow{V_i}\).
Or on a \(V_{1x}<V_{2x}<V_{3x}<V_{4x}\). Donc, le plus grand produit scalaire est celui avec \(\overrightarrow{V_4}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient les vecteurs représentés ci-dessous.
Sans faire de calcul, mais en raisonnant à partir de vos connaissances sur le produit scalaire, dire quel produit scalaire a la valeur la plus élevée dans la liste suivante.
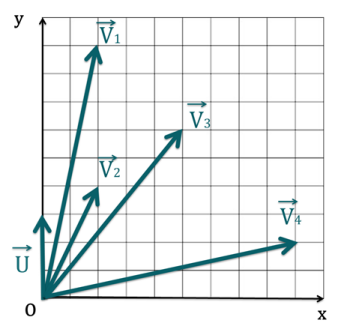
Correction
Explication Générale
Tous les produits scalaires sont calculés avec \(\overrightarrow{U}\) qui est parallèle à l'axe des \(y\).
Pour déterminer le produit scalaire le plus élevé on compare les composantes selon y des vecteurs \(\overrightarrow{V_i}\).
Or on a \(V_{4y}<V_{2y}<V_{3y}<V_{1y}\). Donc, le plus grand produit scalaire est celui avec \(\overrightarrow{V_1}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient les vecteurs représentés ci-dessous.
Sans faire de calcul, mais en raisonnant à partir de vos connaissances sur le produit scalaire, dire quels produits scalaires ont la même valeur.

Correction
Explication Générale
Comme tous les produits scalaires sont calculés par rapport à \(\overrightarrow{U}\), pour déterminer les valeurs des produits scalaires on s’intéresse à la valeur de \(||\overrightarrow{V_i}||.\cos (\overrightarrow{U}. \overrightarrow{V_i})\). Cette grandeur est la projection du vecteur \(\overrightarrow{V_i}\) sur l'axe \(Ox\).
Seuls les vecteurs \(\overrightarrow{V_2}\) et \(\overrightarrow{V_3}\) ont la même coordonnée selon \(Ox\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient les vecteurs représentés ci-dessous.
Sans faire de calcul, mais en raisonnant à partir de vos connaissances sur le produit scalaire, dire quels produits scalaires ont la même valeur.
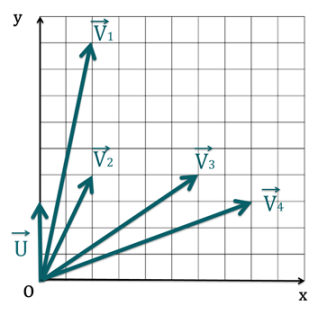
Correction
Explication Générale
Comme tous les produits scalaires sont calculés par rapport à \(\overrightarrow{U}\), pour déterminer les valeurs des produits scalaires on s’intéresse à la valeur de \(||\overrightarrow{V_i}||.\cos (\overrightarrow{U}. \overrightarrow{V_i})\). Cette grandeur est obtenue en projetant le vecteur \(\overrightarrow{V_i}\) sur l'axe \(Oy\). Seuls les vecteurs \(\overrightarrow{V_2}\) et \(\overrightarrow{V_3}\) ont la même coordonnée selon \(Oy\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient les vecteurs représentés ci-dessous. Ils ont tous la même norme.
Parmi les produits scalaires suivants, lequel(s) est (sont) le(s) plus grand(s) ?
Correction
Explication Générale
Comme les vecteurs ont la même norme, il suffit de comparer les angles entre les vecteurs. Le produit scalaire le plus élevé sera celui pour lequel l'angle est aigu (le cosinus sera strictement positif) et le plus petit possible (le cosinus sera le plus grand). L'angle entre \(\overrightarrow{U_1}\) et \(\overrightarrow{U_3}\) est le même que celui entre \(\overrightarrow{U_1}\) et \(\overrightarrow{U_5}\). Les deux réponses sont justes.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Parmi les produits scalaires suivants, lesquels sont positifs ?
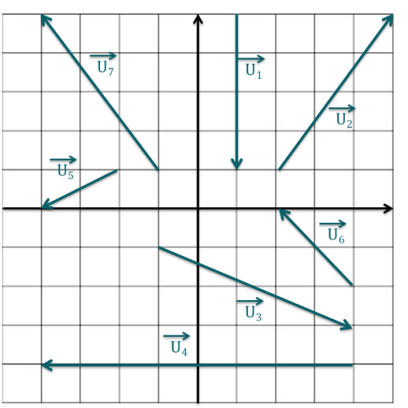
Correction
Explication Générale
À savoir : Pour que le produit scalaire entre deux vecteurs soit positif, il suffit que l'angle formé par les deux vecteurs à partir d'un même point d'application soit aigu (compris entre 0 et 90°). C'est-à-dire que les deux vecteurs pointent vers le même cadran, par exemple les deux vers "en haut, à droite".
Réciproquement, si l'angle entre les vecteurs est compris entre 90° et 180°, alors le produit scalaire sera négatif.
Cela se démontre à partir de la formule du produit scalaire : \(\overrightarrow{u}\cdot\overrightarrow{v}=||\overrightarrow{u}||\cdot||\overrightarrow{v}||\cdot\cos(\overrightarrow{u},\overrightarrow{v})\) où le cosinus est positif si l'angle est aigu (compris entre 0 et 90° en valeur absolue).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient les vecteurs représentés ci-dessous.
Parmi les produits scalaires suivants, lesquels sont négatifs ?

Correction
Explication Générale
À savoir : Pour que le produit scalaire entre deux vecteurs soit positif, il suffit que l'angle formé par les deux vecteurs à partir d'un même point d'application soit aigu (compris entre 0 et 90°). C'est-à-dire que les deux vecteurs pointent vers le même cadran, par exemple les deux vers "en haut, à droite".
Réciproquement, si l'angle entre les vecteurs est compris entre 90° et 180°, alors le produit scalaire sera négatif.
Cela se démontre à partir de la formule du produit scalaire : \(\overrightarrow{u}\cdot\overrightarrow{v}=||\overrightarrow{u}||\cdot||\overrightarrow{v}||\cdot\cos(\overrightarrow{u},\overrightarrow{v})\) où le cosinus est positif si l'angle est aigu (compris entre 0 et 90° en valeur absolue).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient les vecteurs forces représentés ci-dessous.
Parmi les produits scalaires suivants, lesquels sont négatifs ?
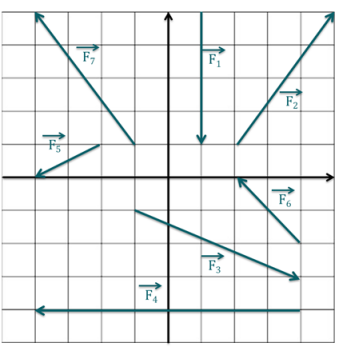
Correction
Explication Générale
À savoir : Pour que le produit scalaire entre deux vecteurs soit positif, il suffit que l'angle formé par les deux vecteurs à partir d'un même point d'application soit aigu (compris entre 0 et 90°). C'est-à-dire que les deux vecteurs pointent vers le même cadran, par exemple les deux vers "en haut, à droite".
Réciproquement, si l'angle entre les vecteurs est compris entre 90° et 180°, alors le produit scalaire sera négatif.
Cela se démontre à partir de la formule du produit scalaire : \(\overrightarrow{u}\cdot\overrightarrow{v}=||\overrightarrow{u}||\cdot||\overrightarrow{v}||\cdot\cos(\overrightarrow{u},\overrightarrow{v})\) où le cosinus est positif si l'angle est aigu (compris entre 0 et 90° en valeur absolue).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient les vecteurs représentés ci-dessous. Ils n'ont pas tous la même norme.
Parmi les produits scalaires suivants, lequel est le plus grand ?
Correction
Explication Générale
Des propositions données, seuls \(\overrightarrow{U_1}.\overrightarrow{U_3}\),\( \overrightarrow{U_1}.\overrightarrow{U_5}\) sont positifs. Comme \(\overrightarrow{U_1}\) est vertical orienté dans le même sens que les deux vecteurs, il suffit de regarder la longueur de la cordonnée verticale. C'est donc \(\overrightarrow{U_1}.\overrightarrow{U_3}\) qui est le plus grand produit scalaire.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient les vecteurs représentés ci-dessous. Ils ont tous la même norme.
Parmi les produits scalaires suivants, lequel est le plus petit ?
Correction
Explication Générale
Des propositions données, seuls \(\overrightarrow{U_1}.\overrightarrow{U_2}\) et \( \overrightarrow{U_1}.\overrightarrow{U_6}\) sont négatifs. Par contre, l'angle entre \( \overrightarrow(U_1)\) et \(\overrightarrow{U_2}\) est plus grand que celui entre \(\overrightarrow(U_1\)) et \(\overrightarrow{U_6}\). Donc \( \overrightarrow{U_1}.\overrightarrow{U_2} < \overrightarrow{U_1}.\overrightarrow{U_6}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit une masse positionnée en \(A\) qui subit une force \(\overrightarrow{F}\) et qui se déplace de \(A\) vers \(B\).
Le travail d'une force \(\overrightarrow{F}\) sur un chemin (\(AB\)) est donné par la formule \(W = \overrightarrow{F}.\overrightarrow{AB}\).
Plusieurs déplacements sont possibles (vers le point \(B_1, B_2, B_3, B_4, B_5, B_6\) ou \(B_7\)) (cf schéma).
Pour quel(s) déplacement(s) le travail de la force\( \overrightarrow{F}\) sera-t-il le plus important ?
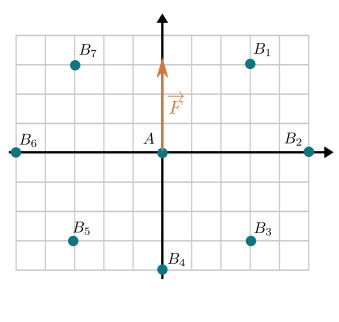
Correction
Explication Générale
Le travail est défini dans l'énoncé comme le produit scalaire entre le vecteur force \(\overrightarrow{F}\) et le vecteur déplacement \(overrightarrow{AB_i}\).
Quand \(\overrightarrow{F} \bot \overrightarrow{AB_i}\), leur produit scalaire est nul.
Quand l'angle entre \(\overrightarrow{F}\) et \(\overrightarrow{AB_i}\) est compris entre 90° et 180° : le produit scalaire est négatif, et donc plus petit qu'un produit scalaire positif.
\(\overrightarrow{AB_1}\) et \(\overrightarrow{AB_2}\) sont de même norme et font le même angle avec \( \overrightarrow{F}\), donc \(\overrightarrow{F}\).\(\overrightarrow{AB_1} = \overrightarrow{F}\).\(\overrightarrow{AB_7}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Un hélicoptère peut se déplacer horizontalement ou verticalement dans un plan vertical. On note \(\overrightarrow{H}\) son déplacement vertical orienté vers le haut, \(\overrightarrow{B}\) son déplacement vertical orienté vers le bas, \(\overrightarrow{D}\) son déplacement horizontal orienté à droite et \(\overrightarrow{G}\) son déplacement horizontal orienté à gauche.
La gravitation exerce une force \(\overrightarrow{P}\) verticale orientée vers le bas.
Le travail d'une force \(\overrightarrow{P}\) sur un trajet \(\overrightarrow{T}\) est donnée par le produit scalaire \(\overrightarrow{P}.\overrightarrow{T}\).
Dans quel(s) cas le travail de la force de gravité est-il nul ?
Correction
Explication Générale
Le produit scalaire de deux vecteurs est nul lorsque les deux vecteurs sont orthogonaux. Dans ce cas, la gravité exerce une force verticale vers le bas. Si le travail de la gravité pendant le déplacement est nul, c'est que le déplacement se fait de manière orthogonale à la force, c'est-à-dire horizontalement vers la droite ou vers la gauche.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient trois vecteurs : \(\overrightarrow{U}, \overrightarrow{V}\) et \(\overrightarrow{W}\).
Quel schéma correspond à la construction permettant d'obtenir \(\overrightarrow{W} = \overrightarrow{U} + \overrightarrow{V}\) ?
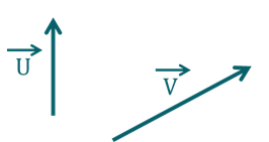
Correction
Explication Générale
Les vecteurs s'ajoutent graphiquement en reliant la "tête" du premier à la "queue' du suivant.
Voir le cours unisciel : http://uel.unisciel.fr/physique/outils_nancy/outils_nancy_ch03/co/apprendre_02_01.html.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient trois vecteurs : \(\overrightarrow{U}\), \(\overrightarrow{V}\) et \(\overrightarrow{W}\).
Quel schéma correspond à la construction permettant d'obtenir \(\overrightarrow{W} = \overrightarrow{V} - \overrightarrow{U}\) ?
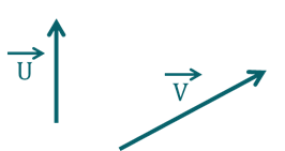
Correction
Explication Générale
Il faut représenter le vecteur \(- \overrightarrow{U}\) . Les vecteurs s'ajoutent graphiquement en reliant la "tête" du premier à la "queue' du suivant.
Voir la ressource en ligne : http://uel.unisciel.fr/physique/outils_nancy/outils_nancy_ch03/co/apprendre_02_01.html.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient deux vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\) non nuls et a un nombre réel non nul.
Dans quelle situation on ne peut pas trouver \(a\) tel que \(\overrightarrow{U}+a.\overrightarrow{V}=\vec 0\) ?
Correction
Explication Générale
Si deux vecteurs sont colinéaires (même direction), alors il sera toujours possible d'en construire une somme égale au vecteur nul.
Si deux vecteurs ne sont pas colinéaires (ils n'ont pas la même direction), alors il sera toujours impossible d'en construire une somme égale au vecteur nul.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Quelles sont la(es) condition(s) pour que la somme de deux vecteurs non nuls et de même norme fasse le vecteur nul \(\overrightarrow{0}\) ?
Correction
Explication Générale
À savoir : Pour que deux vecteurs soient de somme nulle, c'est à dire que \(\overrightarrow{U} + \overrightarrow{V} = \overrightarrow 0\), il faut qu'en plus d'être de même norme non nulle, les deux vecteurs soient colinéaires et de sens opposé.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Quelles sont les affirmations correctes parmi les phrases ci-dessous ?
Correction
Explication Générale
À savoir : La composante horizontale d'une somme de vecteurs est égale à la somme des composantes horizontales des vecteurs.
Mathématiquement cela se traduit par : \(\left(\overrightarrow{A+B}\right)_x=A_x+B_x\).
Plus généralement, l'opération correspondant à prendre la composante horizontale (ou verticale) d'un vecteur est une application linéaire : \(\left(\overrightarrow{A}+\lambda\overrightarrow{B}\right)_x=A_x+\lambda\cdot B_x\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Quelles sont les affirmations correctes parmi les phrases ci-dessous ?

Correction
Explication Générale
À savoir : La composante horizontale d'une somme de vecteurs est égale à la somme des composantes horizontales des vecteurs.
Mathématiquement cela se traduit par : \(\left(\overrightarrow{A+B}\right)_x=A_x+B_x\).
Plus généralement, l'opération correspondant à prendre la composante horizontale (ou verticale) d'un vecteur est une application linéaire : \(\left(\overrightarrow{A}+\lambda\overrightarrow{B}\right)_x=A_x+\lambda\cdot B_x\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Quelles sont les affirmations correctes parmi les phrases ci-dessous ?

Correction
Explication Générale
À savoir : La composante horizontale d'une somme de vecteurs est égale à la somme des composantes horizontales des vecteurs.
Mathématiquement cela se traduit par : \(\left(\overrightarrow{A+B}\right)_x=A_x+B_x\).
Plus généralement, l'opération correspondant à prendre la composante horizontale (ou verticale) d'un vecteur est une application linéaire : \(\left(\overrightarrow{A}+\lambda\overrightarrow{B}\right)_x=A_x+\lambda\cdot B_x\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Quelles sont les affirmations correctes parmi les phrases ci-dessous ?

Correction
Explication Générale
À savoir : La composante horizontale d'une somme de vecteurs est égale à la somme des composantes horizontales des vecteurs.
Mathématiquement cela se traduit par : \(\left(\overrightarrow{A+B}\right)_x=A_x+B_x\).
Plus généralement, l'opération correspondant à prendre la composante horizontale (ou verticale) d'un vecteur est une application linéaire : \(\left(\overrightarrow{A}+\lambda\overrightarrow{B}\right)_x=A_x+\lambda\cdot B_x\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient trois vecteurs : \(\overrightarrow{U}, \overrightarrow{V}\) et \(\overrightarrow{W}\).
Quelle construction correspond à la construction de \(\overrightarrow{W} = \overrightarrow{U} - \overrightarrow{V}\) ?
Correction
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Trois forces agissent en un point P comme représenté sur la figure. Ces trois forces sont dans un même plan.
Que peut on dire de la norme du vecteur force \(\overrightarrow{F}=\overrightarrow{T_1}+\overrightarrow{T_2}+\overrightarrow{T_3}\) ?
Correction
Explication Générale
On trouve les composantes du vecteur somme en additionnant les composantes de chacun des vecteurs : \(\overrightarrow{T_{1x}}+\overrightarrow{T_{2x}}+\overrightarrow{T_{3x}}=4+0-2=2\) et \(\overrightarrow{T_{1y}}+\overrightarrow{T_{2y}}+\overrightarrow{T_{3y}}=0+2-1=1\).
On a donc \(\overrightarrow{F}=2\overrightarrow{u_x}+1\overrightarrow{u_y}\).
On a donc : \(||\overrightarrow{F}||=\sqrt{2^2+1^2}=\sqrt{5}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit \(\overrightarrow{S}\)= \(\overrightarrow{A} +\overrightarrow{B} +\overrightarrow{C} + \overrightarrow{D}+ \overrightarrow{E}+\overrightarrow{F}\).
Quelle construction permet d'obtenir le vecteur \(\overrightarrow{S}\) ?
Correction
Explication Générale
Pour sommer des vecteurs on relie la "tête" du précédent à la "queue" du suivant. Voir le cours unisciel http://uel.unisciel.fr/physique/outils_nancy/outils_nancy_ch03/co/apprendre_02_01.html.
?Représenter une grandeur physique avec un vecteur
Énoncé
Un ballon est lancé par un enfant, vers le haut.
Qu'elles sont les affirmations exactes sur le vecteur vitesse du ballon ?
Correction
Explication Générale
La direction d'un vecteur est la droite support du vecteur (ici la droite verticale).
Le sens d'un vecteur indique vers où pointe le vecteur (ici vers le haut).
?Représenter une grandeur physique avec un vecteur
Énoncé
Calculatrice autorisée
On suit l'évolution de la norme du vecteur vitesse d'un parachutiste qui saute d'un avion et descend vers le sol sur le graphe ci dessous:
Quelles sont les phrases exactes concernant le sens du vecteur vitesse ?
Correction
Explication Générale
Le sens d'un vecteur indique vers où pointe le vecteur.
Le parachutiste se déplace du haut vers le bas. Le vecteur vitesse est toujours dans la direction du mouvement donc vers le bas.
?Représenter une grandeur physique avec un vecteur
Énoncé
Calculatrice autorisée
Un ballon de foot lors d'un tir est soumis à son poids. Le poids est représenté par un vecteur vertical descendant de norme constante (4 N ). Voici quelques graphes liés à ce problème.
Quelles sont les propositions exactes ?
Correction
Explication Générale
La norme d'un vecteur correspond à sa "taille" ici 4 N et est toujours positive
La coordonnée d'un vecteur est positive ou négative et dépend du repère choisi.
Le poids est toujours un vecteur vertical, descendant.
?Représenter une grandeur physique avec un vecteur
Énoncé
Calculatrice autorisée
La 3e loi de Newton indique que si deux objets A et B sont en interaction gravitationnelle, les vecteurs \(\vec{F}_{A/B}\) force que l'objet A exerce sur l'objet B et \(\vec{F}_{B/A}\) force que l'objet B exerce sur l'objet A vérifient la relation
\(\vec{F}_{A/B}=-\vec{F}_{B/A}\)
Quelles sont les propositions qui sont compatibles avec la 3e loi de Newton ?
Correction
Explication Générale
Il faut lutter contre l'idée commune que l'objet le plus lourd « agit plus » que l'objet le plus léger en matière d'interaction gravitationnelle. C'est faux.
L'interaction gravitationnelle est une interaction qui dépend des 2 objets en présence.
?Représenter une grandeur physique avec un vecteur
Énoncé
Calculatrice autorisée.
Le champ de gravité sur la Terre \(\vec{g}\) permet de faire le lien entre le poids \(\vec{P}\) d'un objet sur Terre et sa masse m selon la relation :\( \vec{P} = m \vec{g}\)
Quel est le tableau qui représente les relations exactes entre les différentes caractéristiques des vecteurs \(\vec{g}\) et \(\vec{P}\) ?
Correction
Explication Générale
Comme la masse est une grandeur positive, les vecteurs poids et champ de gravité ont même direction, même sens .
Seules leurs normes diffèrent.
?Représenter une grandeur physique avec un vecteur
Énoncé
La force électrostatique \( \vec{F}\) qui s'exerce sur une particule de charge positive q placée dans un champ \( \vec{E}\) vérifie la relation :\( \vec{E} ={ \vec{F}\over q}\)
Quelle est l'affirmation exacte sur \(\vec{F}\) et \( \vec{E}\) ?
Correction
Explication Générale
Comme la charge de la particule est ici une grandeur positive, les vecteurs force et champ électrostatique ont même direction, même sens .
Seules leurs normes diffèrent.
?Représenter une grandeur physique avec un vecteur
Énoncé
La force électrostatique \( \vec{F}\) qui s'exerce sur une particule de charge q placée dans un champs \( \vec{E}\) vérifie la relation :\( \vec{F} = q \vec{E}\)
Le champ électrostatique \(\vec{E}\) est constant.
La particule étudiée est
soit un proton de charge positive \(q= 1,6,10^ {-19} C\)
soit un électron de charge négative \(q= -1,6.10^{-19} C\)
Quelles sont les caractéristiques de la force \(\vec{F}\) qui sont identiques que la particule soit un proton ou un électron ?
Correction
Explication Générale
Le signe de la charge de la particule ne modifie pas ni la norme, ni la direction des vecteurs force et champs électrostatique, par contre il faut tenir compte de ce signe pour étudier le sens des vecteurs.
?Représenter une grandeur physique avec un vecteur
Énoncé
Calculatrice autorisée.
Le poids \( \vec{P}\) qui s'exerce sur une particule de masse m placée dans un champ \(\vec{g}\) vérifie la relation :\( \vec{P} = m \vec{g}\)
Le champ gravitationnel \(\vec{g}\) est constant.
La particule étudiée est
soit un proton de masse \(m= 1,6,10^ {-27} kg\)
soit un électron de masse \(m= 9,1.10^{-31} kg\)
Quelles sont les caractéristiques du poids \(\vec{P}\) qui sont identiques que la particule soit un proton ou un électron ?
Correction
Explication Générale
La masse est positive pour les 2 particules , donc sens et direction du vecteur poids seront identiques.
Par contre la valeur de la masse est différente pour les 2 particules donc la norme du vecteur poids variera en fonction de la particule.
?Représenter une grandeur physique avec un vecteur
Énoncé
Le poids \( \vec{P}\) d'un objet de masse m dans dans un repère orthonormé\( (O ;\vec {i} ; \vec{ j} ; \vec {k})\) est donné par la relation \( \vec{P} = m \cdot g \cdot\vec{k}\)
Quelles sont les valeurs nécessaires au calcul de la norme du poids ?
Correction
Explication Générale
À savoir : les vecteurs unitaires de la base orthonormée peuvent être appelés :
\((\overrightarrow i,\overrightarrow j,\overrightarrow k)\)
\((\overrightarrow {u_x},\overrightarrow {u_y},\overrightarrow {u_z})\)
\((\overrightarrow {e_x},\overrightarrow {e_y},\overrightarrow {e_z})\)
Ces vecteurs indiquent les directions des trois axes du repères et leur norme vaut \(1 \): \(||\overrightarrow i||=||\overrightarrow j||=||\overrightarrow k||=1\)
?Représenter une grandeur physique avec un vecteur
Énoncé
Une planète A dont le centre de gravité est au point \(O_A\) exerce une force d'attraction gravitationnelle sur une planète B dont le centre de gravité est au point \(O_B\) . cette force est représentée sur le schéma ci dessous :
Quelles sont les formes d'écriture que l'on peut utiliser pour noter ce vecteur force ?
Correction
Explication Générale
À savoir : Il existe deux types de vecteurs.
Des vecteurs qui modélisent un déplacement et qui sont notés avec deux lettres (point de départ et point d'arrivée) comme le vecteur \(\overrightarrow{OM}\) ou le vecteur \(\overrightarrow{AB}\). La norme de ces vecteurs est homogène à une distance (unité = mètre ou km ou ...)
Des vecteurs qui ne modélisent pas un déplacement mais qui modélisent une grandeur physique. Leur norme n'est pas homogène à une distance. C'est le cas par exemple de la force (norme en Newton) ou de la vitesse (norme en m/s). Ces vecteurs sont notés avec une lettre majuscule et parfois du texte en indice. Ex : \(\overrightarrow{F_{A/B}}\) ; \(\overrightarrow{V}}\) ; \(\overrightarrow{E_{1}}\)
?Représenter une grandeur physique avec un vecteur
Énoncé
Calculatrice autorisée
L'objet ponctuel A exerce une force attractive sur l'objet ponctuel B. Cette force est notée \( \vec F_{A/B}.\)
Le vecteur \( \overrightarrow {AB}\) est noté en utilisant le bipoint \((A , B)\)
Que peut on dire de ces 2 grandeurs vectorielles ?
Correction
Explication Générale
La notation du vecteur avec des bipoints utilisée en math, n'a rien à voir avec la notation des forces en physique même si on voit apparaître deux points (A et B)
?Représenter une grandeur physique avec un vecteur
Énoncé
Un ressort exerce une tension \(\vec T\) de 0,5 N sur un objet.
Quelles sont les écritures mathématiques cohérentes avec l'énoncé ?
Correction
Explication Générale
À savoir :
Un vecteur qui modélise une grandeur physique est noté par une lettre avec une flèche. Exemple : \(\overrightarrow{T}\)
La norme d'un vecteur représente la "longueur" de ce vecteur, elle s'écrit soit avec une double barre de chaque côté du vecteur (ex : \(||\overrightarrow T||\) soit juste avec la lettre (\(T\)) et sa valeur numérique est toujours donnée avec une unité.
On ne peut jamais avoir dans une expression une flèche d'un côté du signe égal et pas de l'autre. Un vecteur n'est pas de même nature qu'un nombre !
?Représenter une grandeur physique avec un vecteur
Énoncé
Calculatrice autorisée
On suit l'évolution de la norme du vecteur vitesse d'un parachutiste qui saute d'un avion et descend vers le sol sur le graphe ci dessous:
Quelles sont les phrases exactes concernant la coordonnée \(V_z\) du vecteur vitesse selon l'axe \(Oz\) (axe vertical dirigé vers le haut)?
Correction
Explication Générale
Le parachutiste se déplace du haut vers le bas. Le vecteur vitesse est toujours dans la direction du mouvement donc vers le bas.
La coordonnée \(V_z\) du parachutiste est donc toujours négative.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Dans la base orthonormée \(\left( \overrightarrow{e_x},\overrightarrow{e_z}\right)\). on définit les vecteurs \(\overrightarrow{P}\), \(\overrightarrow{R}\), \(\overrightarrow{N}\) et \(\overrightarrow{OX}\) définis par leurs composantes :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) , \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\), \(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\)
Sans faire de calcul, quels sont les produits scalaires non nuls ?
Correction
Explication Générale
À savoir : Le produit scalaire de deux vecteurs orthogonaux est nul.
À savoir : À 2D, quand l'une des composantes est nulle, le vecteur est porté par une droite parallèle à l'un des axes :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) et \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\) sont des vecteurs verticaux
\(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\) sont des vecteurs horizontaux
Le produit scalaire de deux vecteurs horizontaux, ou de deux vecteurs verticaux sera différent de zéro et le produit scalaire d'un vecteur horizontal et d'un vecteur vertical sera nul.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On peut modéliser les actions agissant sur un avion qui se pose sur le pont d'un porte-avion par 3 forces :
Son poids \(\overrightarrow{P}\)
La réaction normale de la piste \(\overrightarrow{N}\)
La force exercée par le filin sur la crosse d’appontage : \(\overrightarrow{R}\)
La position de l'avion au cours du temps est repérée par sa position \(\overrightarrow{OX(t)}\)
Dans la base orthonormée \(\left( \overrightarrow{e_x},\overrightarrow{e_z}\right)\)., l'expression de ces vecteurs est :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) , \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\), \(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX(t)}=\begin{pmatrix} x(t)\\0\end{pmatrix}\)
Quels sont les produits scalaires non nuls ?
Correction
Explication Générale
À savoir : Le produit scalaire de deux vecteurs orthogonaux est nul.
À savoir : À 2D, quand l'une des composantes est nulle, le vecteur est porté par une droite parallèle à l'un des axes :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) et \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\) sont des vecteurs verticaux
\(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\) sont des vecteurs horizontaux
Le produit scalaire de deux vecteurs horizontaux, ou de deux vecteurs verticaux sera différent de zéro et le produit scalaire d'un vecteur horizontal et d'un vecteur vertical sera nul.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Quelles sont les situations dans lesquelles les vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\) sont colinéaires ?

Correction
Explication Générale
Deux vecteurs sont colinéaires s'ils ont la même direction, c'est-à-dire s'ils sont portés par des droites parallèles.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Dans la base orthonormée \(\left( \overrightarrow{e_x},\overrightarrow{e_z}\right)\). on définit les vecteurs \(\overrightarrow{P}\), \(\overrightarrow{R}\), \(\overrightarrow{N}\) et \(\overrightarrow{OX}\) définis par leurs composantes :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) , \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\), \(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\)
Quels sont les vecteurs horizontaux ?
Correction
Explication Générale
À savoir : À 2D, quand l'une des composantes est nulle, le vecteur est porté par une droite parallèle à l'un des axes. La première composante correspond à l'axe horizontal (axe des \(x\)) et la deuxième composante correspond à l'axe vertical (axe des \(y\)).
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) et \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\) sont des vecteurs verticaux
\(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\) sont des vecteurs horizontaux
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Dans la base orthonormée \(\left( \overrightarrow{e_x},\overrightarrow{e_z}\right)\). on définit les vecteurs \(\overrightarrow{P}\), \(\overrightarrow{R}\), \(\overrightarrow{N}\) et \(\overrightarrow{OX}\) définis par leurs composantes :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) , \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\), \(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\)
Quels sont les vecteurs verticaux ?
Correction
Explication Générale
À savoir : À 2D, quand l'une des composantes est nulle, le vecteur est porté par une droite parallèle à l'un des axes. La première composante correspond à l'axe horizontal (axe des \(x\)) et la deuxième composante correspond à l'axe vertical (axe des \(y\)).
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) et \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\) sont des vecteurs verticaux
\(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\) sont des vecteurs horizontaux
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Dans la base orthonormée \(\left( \overrightarrow{e_x},\overrightarrow{e_z}\right)\). on définit les vecteurs \(\overrightarrow{P}\), \(\overrightarrow{R}\), \(\overrightarrow{N}\) et \(\overrightarrow{OX}\) définis par leurs composantes :
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) , \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\), \(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\)
Quels sont les vecteurs colinéaires?
Correction
Explication Générale
À savoir : À 2D, quand l'une des composantes est nulle, le vecteur est porté par une droite parallèle à l'un des axes. La première composante correspond à l'axe horizontal (axe des \(x\)) et la deuxième composante correspond à l'axe vertical (axe des \(y\)).
\(\overrightarrow{P}=\begin{pmatrix} 0\\-mg\end{pmatrix}\) et \(\overrightarrow{N}=\begin{pmatrix} 0\\+mg\end{pmatrix}\) sont des vecteurs verticaux
\(\overrightarrow{R}=\begin{pmatrix} -kx\\0\end{pmatrix}\) et \(\overrightarrow{OX}=\begin{pmatrix} x\\0\end{pmatrix}\) sont des vecteurs horizontaux
À savoir : deux vecteurs sont colinéaires quand ils sont dans la même direction, c'est-à-dire que les droites qui les portent sont parallèles.
Questions de compréhension et d'application
?Question
Énoncé
On considère la série statistique à 13 éléments suivante :
\(\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline0.1&0.5&7.1&5.1&0.4&6.4&4.9&5.0&1.4&0.2&0.7&6.2&7.1\\\hline\end{array}\)
Lequel des graphiques suivant peut correspondre à son histogramme (en fréquence) ?
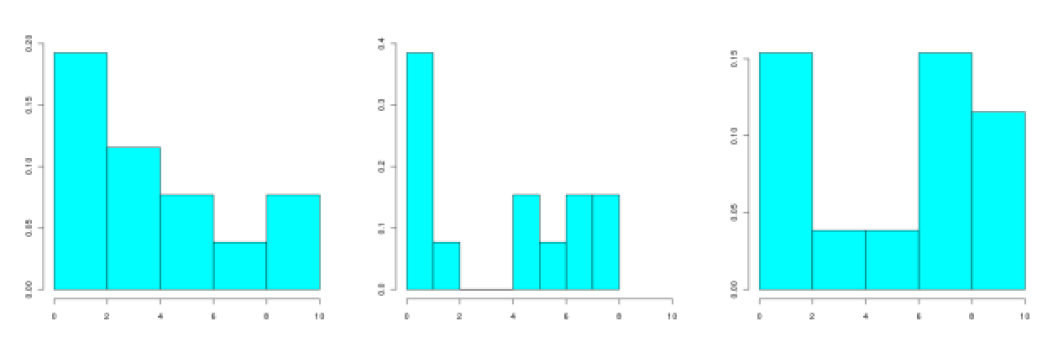
Correction
Explication Générale
Au vu des données, la série ne possède pas d'élément entre 2 et 4.
Les séries associées aux dessins de gauche et de droite contiennent un ou plusieurs éléments entre 2 et 4 ; elles ne peuvent être la bonne réponse.
Le dessin du milieu correspond à la série initiale.
?Question
Énoncé
On considère la série statistique à 13 éléments suivante :
\(\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline6.7&5.2&0.5&5.4&0.5&6.9&7.1&3.0&1.1&0.1&6.2&0.2&4.9\\\hline\end{array}\)
Lequel des graphiques suivant peut correspondre à son diagramme en boîte ?
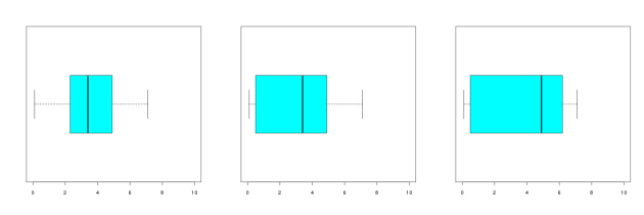
Correction
Explication Générale
Ordonnons la série :
Le premier quartile de la série associée au dessin de gauche est supérieur à 2 ; ce ne peut être la bonne réponse.
La médiane de la série associée au dessin de gauche est inférieure à 4 ; ce ne peut être la bonne réponse.
Le dessin de droite correspond à la série initiale.
?Question
Énoncé
À la dernière épreuve de géographie, un groupe de neuf élèves a obtenu 10 de moyenne avec une variance égale à 10. Les rejoint le meilleur élève de la classe qui a obtenu 20. Calculer à une décimale près la variance des notes de ce groupe de dix élèves.
Correction
Explication Générale
Notons \(\textstyle{s_1}\) et \(\textstyle{s_2}\) (resp. \(\textstyle{t_1}\) et \(\textstyle{t_2}\)
\(\textstyle{s_1=9\times 10=90}\)
\(\textstyle{t_1=s_1+20=110}\)
Rappelons la variance du groupe de 9 élèves est égale à 10
On en déduit :
\(\textstyle{s_2=(10+100)*9=990}\)
\(\textstyle{t_2=s_2+20^2=1390}\)
Le calcul de la variance du groupe de 10 élèves s'en déduit :
\(\frac{t_2}{10}-\left(\frac{t_1}{10}\right)^2=139-11^2=18\)
?Question
Énoncé
On considère deux séries statistiques, l'une de 10 éléments, l'autre de 15, ayant le même écart-type égal à 5. On réunit les deux séries en une seule de 25 éléments. A-t-elle encore un écart-type égal à 5 ?
Correction
Explication Générale
Ce serait vrai si (et seulement si) les moyennes étaient égales, ce qui n'est pas indiqué. Considérons le plus simple des contre-exemples, celui de deux séries à un élément. Elles sont toutes deux de variance nulle. Mais la série à deux éléments issue de leur réunion a une variance non nulle si ces deux éléments sont distincts.
?Question
Énoncé
La publicité pour une lotion capillaire anti-chute annonce 80% de résultats positifs. Après un essai sur un échantillon aléatoire et simple de 100 personnes, 74 ont observé un effet positif. Si l'on suppose l'échantillon aléatoire représentatif, à quel(s) seuil(s) peut-on considérer la publicité comme mensongère ?
Pour le déterminer, on ne considérera que des intervalles de fluctuation symétriques et on pourra s'aider du tableau des fréquences cumulées de la loi normale centrée réduite :
\(\begin{array}{|c||c|c|c|c|}\hline x&0.84&1.28&1.64&1.96\\ \hline\mathbb P(X\leq x)&0.80&0.90&0.95&0.975\\\hline\end{array}\)
avec \(\textstyle{X\sim\mathcal N(0,1)}\)
Correction
Explication Générale
Si la publicité ne ment pas, le nombre \(\textstyle{N}\) de personnes de l'échantillon ayant observé un effet positif suit une loi binomiale de paramètres \(\textstyle{100}\) et \(\textstyle{0.8}\) . Les conditions ( \(\textstyle{100\geq 30}\) , \(\textstyle{100\times 0.8\geq 5}\) , \(\textstyle{100\times 0.2\geq 5}\) sont vérifiées pour permettre de construire un intervalle de fluctuation à partir des quantiles de la loi normale. On a donc :
\( \mathbb P\left(\frac N{100}\in\left[0.8-0.04u_\alpha,0.8+0.04u_\alpha\right]\right)\simeq1-u_\alpha\)
avec \(\textstyle{0.04=\sqrt{\frac{0.8\times0.2}{100}}}\) et \(\textstyle{u_\alpha}\) tel que \(\textstyle{\mathbb P(-u_\alpha\leq X\leq u_\alpha)=1-\alpha}\) où \(\textstyle{X}\) suit une loi \(\textstyle{\mathcal N(0,1)}\)
Dans le cas présent, \(\textstyle{\frac N{100}}\) prend la valeur \(\textstyle{0.74}\)
\(\textstyle{u_\alpha=1.96}\) : \(\textstyle{1-\alpha}\) vaut alors \(\textstyle{0.95}\) ; l'Intervalle de confiance au seuil \(\textstyle{0.95}\) vaut \(\textstyle{[0.72,0.88]}\) ; la fréquence observée est dans l'intervalle de fluctuation, on peut donc supposer que la publicité dit vrai. C'est vrai aussi au seuil \(\textstyle{0.975}\)
\(\textstyle{u_\alpha=1.64}\) : \(\textstyle{1-\alpha}\) vaut alors \(\textstyle{0.90}\) ; l'intervalle de fluctuation au seuil \(\textstyle{0.90}\) vaut \(\textstyle{[0.73,0.87]}\)
\(\textstyle{u_\alpha=1.28}\) : \(\textstyle{1-\alpha}\) vaut alors \(\textstyle{0.80}\) ; l'intervalle de fluctuation au seuil \(\textstyle{0.80}\) vaut \(\textstyle{[0.75,0.85]}\)
la fréquence observée n'est pas dans l'intervalle de confiance, on peut supposer que la publicité ment.
?Question
Énoncé
A l'université, les souris blanches représentent 10% de la population totale de souris. Les étudiants en attrapent 10, toutes grises. Au seuil de 90%, peut-on estimer que ces 10 souris forment un échantillon aléatoire représentatif des souris de l'université ?
\(\begin{array}{|c||c|c|c|c|c|c|c|c|c|c|c|}\hline x&0&1&2&3&4&5&6&7&8&9&10\\\hline\mathbb{P}(X=x)&0.349& 0.387& 0.194& 0.057& 0.011& 0.001& 0.000& 0.000& 0.000& 0.000& 0.000\\\hline\end{array}\)
avec \(\textstyle{X\sim\mathcal{B}(10,0.1)}\)
Correction
Explication Générale
La population de souris étant suffisamment importante à l'université, le nombre \(\textstyle{N}\) de souris blanches attrapées suit une loi binomiale de paramètres \(\textstyle{10}\) et \(\textstyle{0.1}\) . Soit \(\textstyle{I}\) un intervalle de fluctuation au seuil 90% pour \(\textstyle{N}\) . On doit avoir \(\textstyle{\mathbb P(N\in I)\geq 0.9}\) . Or \(\textstyle{\mathbb P(N=0)=0.349}\) , ce qui implique \(\textstyle{0\in I}\) (sinon \(\textstyle{\mathbb P(N\in I)\leq 1-0.348<0.9}\)
Remarquons que le meilleur choix pour un intervalle de fluctuation au seuil 90% est \(\textstyle{[0,2]}\) , et que l'on a \(\textstyle{\mathbb P(N\in[0,2])=0.931\geq0.9}\)
?Question
Énoncé
Les personnes de groupe sanguin A+ constituent 38% de la population française. Donner un intervalle de fluctuation au seuil 90% pour le nombre de personnes de ce groupe sanguin parmi 10 français choisis au hasard, en s'aidant de la table de la loi binomiale de paramètres \(\textstyle{n=10}\) et \(\textstyle{p=0.38}\)
\(\begin{array}{|c||c|c|c|c|c|c|c|c|c|c|c|}\hline x&0&1&2&3&4&5&6&7&8&9&10\\\hline\mathbb{P}(X=x)&0.008&0.051&0.142&0.232&0.249&0.183&0.093&0.033&0.008&0.001&0.000\\\hline\end{array}\)
avec \(\textstyle{X\sim\mathcal{B}(10,0.38)}\)
Correction
Explication Générale
Soit \(\textstyle{N}\) le nombre de personnes du groupe sanguin A+ parmi les 10 personnes tirées au hasard. Rappelons que \(\textstyle{[a ;b]}\) est un intervalle de fluctuation au seuil 90% pour \(\textstyle{N}\) si \(\textstyle{\mathbb P(N\in [a ;b])\geq0.9}\)
Comme les 10 personnes sont tirées au hasard dans une grande population, on peut considérer qu'elles forment un échantillon. Chaque personne ayant la probabilité \(\textstyle{0.38}\) d'être du groupe A+, \(\textstyle{N}\) suit une loi binomiale de paramètres \(\textstyle{10}\) et \(\textstyle{0.38}\)
Calculons \(\textstyle{\mathbb P(N\in[1 ;6])}\)
\(\begin{eqnarray*}\mathbb P(N\in[1 ;6])&=&1-\mathbb P(N\notin[1 ;6])\\&=&1-\mathbb P(N=1)-\mathbb P(N=7)-\cdots-\mathbb P(N=10)\\ &=&1-0.008-0.033-0.008-0.001\\&=&0.95\geq0.9\end{eqnarray*}\)
Il s'agit donc d'un intervalle de fluctuation au seuil \(\textstyle{0.90}\)
\(\textstyle{\mathbb P(N\in[1 ;7])=0.983\geq0.9}\)
\(\textstyle{\mathbb P(N\in[1 ;8])=0.991\geq0.9}\)
\(\textstyle{\mathbb P(N\in[2 ;6])=0.899<0.9}\) ; ce n'est pas un intervalle de fluctuation au seuil \(\textstyle{0.9}\)
\(\textstyle{\mathbb P(N\in[2 ;7])=0.932\geq0.9}\)
\(\textstyle{\mathbb P(N\in[2 ;8])=0.94\geq0.9}\)
?Question
Énoncé
Déterminer un intervalle de fluctuation asymptotique \(\textstyle{I}\)
au seuil 80% pour la fréquence d'un caractère dans un échantillon de taille 100, tiré au hasard dans une population où 50% des individus présentent ce caractère.
On choisira l'intervalle le plus pertinent et on arrondira à deux décimales. On pourra s'aider du tableau des fréquences cumulées de la loi normale centrée réduite :
\(\begin{array}{|c||c|c|c|c|c|}\hline x&0.52&0.84&1.28&1.64&1.96\\ \hline\mathbb P(X\leq x)&0.70&0.80&0.90&0.95&0.975\\\hline\end{array}\)
avec \(\textstyle{X\sim\mathcal N(0,1)}\)
Correction
Explication Générale
Soit \(\textstyle{N}\) le nombre d'occurrences du caractère dans l'échantillon. Il suit une loi binomiale de paramètres \(\textstyle{100}\) et \(\textstyle{0.5}\) . D'après le théorème de Moivre-Laplace, on a pour tout \(\textstyle{a<b}\)
\(\mathbb P\left(\frac{N-100\times 0.5}{\sqrt{100\times 0.5^2}}\in[a ;b]\right)\simeq\mathbb P(X\in[a ;b])\)
D'après le tableau des fréquences cumulées de la loi normale, et du fait qu'elle soit symétrique, on a :
\(\mathbb P(X\in[-1.28,1.28])=\mathbb P(X\leq 1.28)-\mathbb P(X\leq -1.28)=0.9-0.1=0.8\)
Reste à calculer l'intervalle pour \(\textstyle{N}\)
\(\begin{eqnarray*}-1.28\leq\frac{N-100\times 0.5}{\sqrt{100\times 0.5^2}}\leq 1.28\Longleftrightarrow&-1.28\leq\frac{N-50}{5}\leq 1.28\&\Longleftrightarrow&43.6\leq N\leq 56.4\end{eqnarray*}\)
Soit \(\textstyle{f}\) la fréquence du caractère dans l'échantillon. Comme \(\textstyle{f=N/100}\) , on en déduit un intervalle de fluctuation pour \(\textstyle{f}\) au seuil \(\textstyle{0.8}\)
\(\mathbb P(0.436\leq f\leq 0.564)\simeq\mathbb P(X\in[-1.28,1.28])=0.8\)
?Question
Énoncé
Soit \(\textstyle{X}\) une variable aléatoire dont la loi de probabilité est donnée dans le tableau ci-dessous :
\(\textstyle{x=}\) | 1 | 2 | 3 | 4 |
\(\textstyle{\mathbb P(X=x)}\) | \(\textstyle{\frac16}\) | \(\textstyle{\frac12}\) | \(\textstyle{\frac3{10}}\) | \(\textstyle{\frac1{30}}\) |
Correction
Explication Générale
\(\textstyle{\mathbb E[X]=1\times\dfrac16+2\times\dfrac12+3\times\dfrac3{10}+4\times\dfrac1{30}=2,2}\) D'autre part \(\textstyle{\mathbb E\left[X^2\right]=1^2\times\dfrac16+2^2\times\dfrac12+3^2\times\dfrac3{10}+4^2\times\dfrac1{30}=5,4}\) , d'où \(\textstyle{V(X)=5,4-2,2^2=0,56=\dfrac{14}{25}}\) D'où \(\textstyle{\sigma(X)=\sqrt{V(X)}=\dfrac{\sqrt{14}}{5}} \)
?Question
Énoncé
On tire \(\textstyle{2}\) cartes dans un paquet de \(\textstyle{52}\) cartes. La négation de l'événement « on a tiré au moins un as rouge parmi les \(\textstyle{2}\) »
Correction
?Question
Énoncé
On tire \(\textstyle{2}\) cartes dans un paquet de \(\textstyle{52}\)
Correction
?Question
Énoncé
On tire une carte parmi \(\textstyle{52}\)
Correction
?Question
Énoncé
En étudiant une population, on a remarqué que \(\textstyle{40\%}\) des individus font de la natation, \(\textstyle{25\%}\) font du badminton et \(\textstyle{12\%}\) et \(\textstyle{12\%}\) pratiquent les deux sports.
Correction
?Question
Énoncé
On lance un dé non équilibré. On obtient le tableau suivant incomplet :
n° face | 1 | 2 | 3 | 4 | 5 | 6 |
probabilité | 0,1 | 0,1 | 0,4 | 0,15 |
Sachant que l'apparition du 6 est 4 fois plus probable que celle du 3 , la probabilité d'apparition du 3 est :
Correction
Explication Générale
Soit \(\textstyle{x}\) la probabilité d'apparition du 3 , alors celle d'apparition du \(\textstyle{6}\) est \(\textstyle{4x}\).
On a alors : \(0,1+0,1+x+0,4+0,15+4x=1\)
?Question
Énoncé
Une urne contient \(\textstyle{15}\) boules numérotées de \(\textstyle{1}\) à \(\textstyle{15}\) . On extrait au hasard une boule de l'urne. La probabilité de l'événement \(\textstyle{E}\) : « le numéro de la boule est un multiple de \(\textstyle{3}\) ou est supérieur ou égal à \(\textstyle{10}\) vaut :
Correction
Explication Générale
Soit \(\textstyle{A}\) l'événement : « le numéro de la boule est un multiple de \(\textstyle{3}\) » et \(\textstyle{B}\) : « le numéro de la boule est supérieur ou égal à \(\textstyle{10}\) ». Alors \(\textstyle{E=A\cup B}\) et \(\textstyle{\mathbb P(E)=\mathbb P(A)+\mathbb P(B)-\mathbb P(A\cap B)}\)
Le nombre de cas total est \(\textstyle{15}\) et il y a équiprobabilité, d'où \(\textstyle{\mathbb P(E)=\dfrac5{15}+\dfrac6{15}-\dfrac2{15}=\dfrac35}\)
?Question
Énoncé
Une loterie permet de gagner \(\textstyle{5}\) euros , \(\textstyle{7}\) euros , \(\textstyle{10}\) euros ou \(\textstyle{15}\) euros.
gain | 5 | 7 | 10 | 15 |
probabilité | \(\textstyle{\frac35}\) | \(\textstyle{\frac14}\) |
La probabilité de gagner au moins \(\textstyle{10}\) euros est :
Correction
Explication Générale
L'événement contraire de l'événement : « gagner au moins \(\textstyle{10}\) euros » est l'événement : « gagner \(\textstyle{5}\) ou \(\textstyle{7}\) euros ». La probabilité cherchée est donc égale à \(\textstyle{1-\left(\dfrac35+\dfrac14\right)=1-\dfrac{17}{20}=\dfrac3{20}}\)
?Question
Énoncé
On lance successivement \(\textstyle{2}\) dés équilibrés et l'on note la somme obtenue. La probabilité d'obtenir la somme \(\textstyle{6}\) est :
Correction
Explication Générale
On peut représenter les résultats possibles dans un tableau à double entrée où l'on note les sommes obtenues. La somme \(\textstyle{6}\) apparaît autant de fois que la somme \(\textstyle{8}\) , c'est-à-dire qu'il y a autant de couples de nombres dont la somme est \(\textstyle{6}\) que de couples de nombres dont la somme est \(\textstyle{8}\) . L'univers est l'ensemble des couples et il y a équiprobabilité, d'où le résultat. La probabilité d'obtenir la somme \(\textstyle{6}\) est égale à celle d'obtenir \(\textstyle{8}\)

?Question
Énoncé
On dispose d'un cube en bois de \(\textstyle{3}\) cm d'arête, peint en bleu. On le découpe parallèlement aux faces, en \(\textstyle{27}\) cubes de \(\textstyle{1}\) cm d'arête. On place ces \(\textstyle{27}\) cubes dans un sac.
Correction
?Question
Énoncé
On lance cinq fois de suite un dé équilibré. La probabilité d'obtenir deux fois exactement un nombre pair est \(\textstyle{\dfrac5{16}}\)
Correction
Explication Générale
L'épreuve de Bernoulli est le lancer du dé. On appelle succès \(\textstyle{S}\) : « obtenir un nombre pair », donc \(\textstyle{\mathbb P(S)=\dfrac12}\)
On répète la même expérience cinq fois, les résultats étant indépendants. On a donc un schéma de Bernoulli de paramètres \(\textstyle{\left(5;\dfrac12\right)}\)
D'où la probabilité cherchée est \(\textstyle{\left(\begin{array}{c}5\\2\end{array}\right)\left(\dfrac12\right)^2\left(\dfrac12\right)^3=\dfrac5{16}}\)
?Question
Énoncé
Une cible circulaire est composée de trois zones numérotées \(\textstyle{1}\) , \(\textstyle{2}\) , et \(\textstyle{3}\) . La probabilité d'atteindre l'une des zones est proportionnelle au numéro de la zone. On admet que les résultats de plusieurs tirs successifs sont indépendants. La probabilité d'atteindre au moins trois fois la zone numéro \(\textstyle{2}\) au cours de cinq tirs successifs est \(\textstyle{\dfrac{40}{243}}\)
Correction
Explication Générale
L'expérience aléatoire est de tirer une fois sur la cible. On appelle succès \(\textstyle{S}\) l'événement : « tirer dans la zone \(\textstyle{2}\) ». Cherchons \(\textstyle{\mathbb P(S)}\)
Soit \(\textstyle{p}\) la probabilité de tirer dans la zone \(\textstyle{1}\) . Alors la probabilité de tirer dans la zone \(\textstyle{2}\) est \(\textstyle{2p}\) et celle de tirer dans la zone \(\textstyle{3}\) est \(\textstyle{3p}\)
La somme des probabilité est \(\textstyle{1}\) d'où \(\textstyle{p+2p+3p=1}\) , soit \(\textstyle{p=\dfrac16}\)
D'où \(\textstyle{\mathbb P(S)=\dfrac13}\)
Remarque :
On peut aussi écrire la proportionnalité sous la forme : \(\textstyle{\dfrac{\mathbb P(1)}1=\dfrac{\mathbb P(2)}2=\dfrac{\mathbb P(3)}3=\dfrac{\mathbb P(1)+\mathbb P(2)+\mathbb P(3)}{1+2+3}=\dfrac16}\)
Soit \(\textstyle{X}\) la variable aléatoire égale au nombre de succès sur \(\textstyle{5}\) tirs. \(\textstyle{X}\) suit la loi binomiale de paramètres \(\textstyle{\left(5;\dfrac16\right)}\)
La probabilité cherchée est \(\textstyle{\mathbb P(X\geq3)=\mathbb P(X=3)+\mathbb P(X=4)+\mathbb P(X=5)}\) .D'où \(\mathbb P(X\geq3)=\left(\begin{array}{c}5\\3\end{array}\right)\left(\dfrac13\right)^3\left(\dfrac23\right)^2+\left(\begin{array}{c}5\\4\end{array}\right)\left(\dfrac13\right)^4\left(\dfrac23\right)+\left(\begin{array}{c}5\\5\end{array}\right)\left(\dfrac13\right)^5=\dfrac{51}{243}=\dfrac{17}{81}.\)
?Question
Énoncé
Un professeur veut montrer à ses \(\textstyle{35}\) élèves ( \(\textstyle{20}\) filles et \(\textstyle{15}\) garçons) le fonctionnement de la commande « random » de son logiciel de statistique. Il attribue à chaque élève un nombre entier compris entre \(\textstyle{1}\) et \(\textstyle{35}\) . Il interroge durant \(\textstyle{20}\) séances un élève de la classe dont le numéro est déterminé aléatoirement et uniformément à chaque séance par le logiciel. L'espérance du nombre de filles interrogées est inférieure à \(\textstyle{12}\)
Correction
Explication Générale
Pour chaque séance, on appelle succès l'événement \(\textstyle{S}\) : « choisir une fille ». \(\mathbb P(S)=\dfrac47\).
Soit \(\textstyle{X}\) la variable aléatoire qui compte le nombre de succès sur les \(\textstyle{20}\) séances. \(\textstyle{X}\) suit la loi binomiale de paramètres \(\textstyle{\left(20;\dfrac47\right)}\) . Le nombre moyen de filles interrogées est l'espérance de \(\textstyle{X}\)
\(\mathbb E[X]=np=20\times\dfrac47<12\)
?Question
Énoncé
Un revendeur de matériel informatique veut se fournir en clés usb chez un grossiste, où une clé usb sur \(\textstyle{25}\) est défectueuse. Il prélève au hasard, pour les examiner, successivement et avec remise, \(\textstyle{10}\) clés usb chez le grossiste. La probabilité que le revendeur trouve au plus une clé usb défectueuse parmi les \(\textstyle{10}\) prélevées est \(\textstyle{\dfrac1{25}}\)
Correction
Explication Générale
On prélève une clé usb. On appelle succès l'événement \(\textstyle{S}\)
On répète \(\textstyle{10}\) fois la même expérience, les résultats étant indépendants. Soit \(\textstyle{X}\) la variable aléatoire qui compte le nombre de succès. \(\textstyle{X}\) suit la loi binomiale de paramètres \(\textstyle{\left(10;\dfrac1{25}\right)}\)
La probabilité cherchée est \(\textstyle{\mathbb P(X\leq1)}\)
\(\begin{eqnarray*}\mathbb P(X\leq1)&=&\mathbb P(X=0)+\mathbb P(X=1)\\&=&\left(\begin{array}{c}10\\0\end{array}\right)\left(\dfrac{24}{25}\right)^{10}+\left(\begin{array}{c}10\\1\end{array}\right)\left(\dfrac1{25}\right)\left(\dfrac{24}{25}\right)^9\\&\approx&0,94\end{eqnarray*}\)
?Question
Énoncé
\(\textstyle{6}\) étudiants sur \(\textstyle{10}\) d'une école d'ingénieurs sortent diplômés. On choisit au hasard \(\textstyle{7}\) étudiants sortants. Le nombre d'étudiants de cette école est assez important pour pouvoir considérer le choix des étudiants comme des tirages successifs avec remise. La probabilité qu'au moins \(\textstyle{3}\) étudiants parmi les \(\textstyle{7}\) soient diplômés est supérieure à \(\textstyle{0,9}\)
Correction
Explication Générale
On choisit un étudiant. On appelle succès l'événement \(\textstyle{S}\) : « l'étudiant est diplômé ».
\(\mathbb P(S)=0,6\)
On répète \(\textstyle{7}\) fois la même expérience, les résultats étant indépendants d'après l'hypothèse. Soit \(\textstyle{X}\) la variable aléatoire qui compte le nombre de succès. \(\textstyle{X}\) suit la loi binomiale de paramètres \(\textstyle{(7;0,6)}\) . La probabilité cherchée est \(\textstyle{\mathbb P(X\geq3)}\)
Il y a deux méthodes pour calculer cette probabilité :
\(\mathbb P(X\geq 3)=\sum_{k=3}^{k=7}\mathbb P(X=k)\mbox{ ou }\mathbb P(X\geq3)=1-\mathbb P(X<3)\)
La deuxième écriture est moins coûteuse en calculs.
\(\begin{eqnarray*}\mathbb P(X<3)=\mathbb P(X=0)+\mathbb P(X=1)+\mathbb P(X=2)\\=\left(\begin{array}{c}7\\0\end{array}\right)(0,4)^7+\left(\begin{array}{c}7\\1\end{array}\right)(0,6)(0,4)^6+\left(\begin{array}{c}7\\2\end{array}\right)(0,6)^2(0,4)^5\\ \\ \mathbb P(X\geq 3)=1-\mathbb P(X<3)\\ =1-\left((0,4)^7+7(0,6)(0,4)^6+21(0,6)^2(0,4)^5\right)\\\approx0,904\end{eqnarray*}\)
?Question
Énoncé
On place au hasard \(\textstyle{10}\) cahiers dans \(\textstyle{8}\) tiroirs (tous les cahiers peuvent être dans le même tiroir). La probabilité qu'il y ait exactement \(\textstyle{5}\) cahiers dans le premier tiroir est est 0,004 à \(10^{-3}\) près
Correction
Explication Générale
L'expérience aléatoire est de placer un cahier. Le succès \(\textstyle{S}\) est l'événement : « le cahier est dans le premier tiroir ». \(\mathbb P(S)=\dfrac18\)
On répète cette expérience \(\textstyle{10}\) fois, les résultats étant indépendants. On a donc un schéma de Bernoulli de paramètres \(\textstyle{\left(10;\dfrac18\right)}\)
La probabilité cherchée est \(\textstyle{\left(\begin{array}{c}10\\5\end{array}\right)\left(\dfrac18\right)^5\left(\dfrac78\right)^5}\) soit \(\textstyle{252\times\dfrac{7^5}{8^{10}}}\) , c'est-à-dire environ \(\textstyle{0,004}\)
?Question
Énoncé
Un jeu de fête foraine consiste à lancer des balles dans \(\textstyle{2}\) cibles, l'une rouge, la seconde jaune. La probabilité d'atteindre la cible rouge est égale à \(\textstyle{\frac{1}{20}}\) , et celle d'atteindre la jaune est \(\textstyle{\frac{1}{10}}\) . La probabilité d'atteindre la cible jaune au moins \(\textstyle{2}\) fois au cours de 7 lancers est :
Correction
?Question
Énoncé
Une usine fabrique des disques durs. Chaque disque dur fabriqué a une probabilité \(\textstyle{p=\frac{1}{1000}}\) d'être défectueux. On doit inspecter en moyenne \(\textstyle{10^5}\) disques pour obtenir en moyenne 10 défectueux.
Correction
Explication Générale
Supposant les tirages des disques indépendants, la moyenne du nombre de disques défectueux parmi \(\textstyle{n}\) disques est \(\textstyle{\frac{n}{1000}}\)
?Question
Énoncé
Soit un univers muni d'une probabilité \(\textstyle{\mathbb P}\) , \(\textstyle{A}\) et \(\textstyle{B}\) deux événements tels que : \(\textstyle{\mathbb P(A)=0,6}\) , \(\textstyle{\mathbb P_A(B)=0,8}\) et \(\textstyle{\mathbb P_{\overline A}(B)=0,1}\)
Correction
?Question
Énoncé
On tire successivement et sans remise deux cartes parmi \(\textstyle{52}\)
Correction
Explication Générale
Soit \(\textstyle{A}\) l'événement "on tire deux cartes de même couleur". Alors par invariance du problème par permutation des couleurs, \(\textstyle{\mathbb{P}(A)=2\mathbb{P}(\text{on tire deux rouges})}\) . Soit pour \(\textstyle{i\in\{1, 2\}}\) , \(\textstyle{R_i}\) l'événement "la \(\textstyle{i}\) ème carte est rouge". Alors \(\textstyle{\mathbb{P}(A)= 2\mathbb{P}(R_1) \mathbb{P}(R_2\vert R_1)= 2\frac{26}{52}\frac{25}{51}=\frac{25}{51}<\frac{1}{2}}\)
?Question
Énoncé
On tire successivement et sans remise deux cartes parmi \(\textstyle{52}\) . La probabilité de tirer deux noires sachant qu'on a tiré au moins une noire est plus grande que \(\textstyle{\frac{1}{2}}\)
Correction
Explication Générale
En notant \(\textstyle{N_i}\) l'événement "la \(\textstyle{i}\) ème carte est noire" ( \(\textstyle{i\in\{1, 2\}}\) ), la probabilité recherchée est \(\textstyle{\mathbb{P}(N_2\vert N_1)= \frac{25}{51}<\frac{1}{2}}\)
?Question
Énoncé
Un voyageur arrive à un carrefour. Il sait qu'à cet endroit il va trouver deux routes : un cul de sac et la bonne route. Il y a trois frères à ce carrefour : \(\textstyle{F_1}\) , \(\textstyle{F_2}\) et \(\textstyle{F_3}\) . \(\textstyle{F_1}\) dit la vérité une fois sur dix. \(\textstyle{F_2}\) dit la vérité trois fois sur dix. \(\textstyle{F_3}\) dit la vérité neuf fois sur dix. Il n'y a personne d'autre à ce carrefour. Le voyageur s'adresse uniformément au hasard à un et un seul des trois frères. Il lui demande son chemin, et s'aperçoit par la suite que ce chemin est le bon. Quelle est la probabilité qu'il se soit adressé à \(\textstyle{F_1}\)
Correction
Explication Générale
Soit \(\textstyle{C=}\) "le chemin choisi est le bon". Alors \(\textstyle{\mathbb{P}(F_1\vert C)=\frac{\mathbb{P}(F_1\cap C)}{\mathbb{P}(C)}= \frac{\mathbb{P}(C\vert F_1)\mathbb{P}(F_1)}{\mathbb{P}(C\vert F_1)\mathbb{P}(F_1) + \mathbb{P}(C\vert F_2)\mathbb{P}(F_2) + \mathbb{P}(C\vert F_3)\mathbb{P}(F_3)}= \frac{\frac{1}{10}\frac{1}{3}}{\frac{1}{10}\frac{1}{3} + \frac{3}{10}\frac{1}{3} + \frac{9}{10}\frac{1}{3}}= \frac{1}{13}}\)
?Question
Énoncé
On jette successivement deux dés équilibrés. Quelle est la probabilité qu'on obtienne au moins un \(\textstyle{6}\)
Correction
Explication Générale
Soit \(\textstyle{X_i}\) la variable aléatoire donnant le résultat du \(\textstyle{i}\) ème lancer ( \(\textstyle{i\in\{1, 2\}}\) ) et \(\textstyle{D}\) l'événement "les deux résultats sont différents". Alors \(\textstyle{\mathbb{P}(\{X_1=6\}\cup \{X_2=6\}\vert D)= \frac{\mathbb{P}((\{X_1=6\}\cup \{X_2=6\})\cap D)}{\mathbb{P}(D)}= \frac{\mathbb{P}(\{X_1=6\}\cap \{X_2 \neq 6\})+ \mathbb{P}(\{X_1\neq 6\}\cap \{X_2=6\})}{\mathbb{P}(D)}= \frac{2\frac{1}{6}\frac{5}{6}}{\sum_{i=1}^6\mathbb{P}(X_1=i, X_2\neq i)}= \frac{\frac{5}{18}}{\frac{5}{6}}=\frac{1}{3}}\)
?Question
Énoncé
Une épreuve du jeu de Fort Boyard consiste à tenter d'ouvrir la serrure d'un coffre à l'aide de clés qui se ressemblent toutes. Parmi les \(\textstyle{10}\) clés disponibles, une seule ouvre le coffre. Un candidat (un peu stupide) tente d'ouvrir le coffre en choisissant l'une des \(\textstyle{10}\) clés au hasard et uniformément à chaque essai. La probabilité d'ouvrir le coffre au bout de \(\textstyle{3}\) au plus est de
Correction
Explication Générale
Le complémentaire de l'événement en question est "au bout des trois tentatives, le coffre n'est pas ouvert" qui est de probabilité \(\textstyle{\left(\frac{9}{10}\right)^3}\)
?Question
Énoncé
Une épreuve du jeu de Fort Boyard consiste à tenter d'ouvrir la serrure d'un coffre à l'aide de clés qui se ressemblent toutes. Parmi les \(\textstyle{10}\) clés disponibles, une seule ouvre le coffre. Un candidat tente d'ouvrir le coffre en mettant de côté au fur et à mesure les mauvaises clés et en choisissant au hasard et uniformément une clé parmi les clés restantes à chaque essai. La probabilité d'ouvrir le coffre au bout de \(\textstyle{3}\) au plus est de
Correction
Explication Générale
La probabilité en question est égale à \(\textstyle{\frac{1}{10}+ \frac{9}{10}\frac{1}{9}+ \frac{9}{10}\frac{8}{9}\frac{1}{8}= \frac{3}{10}}\)
?Question
Énoncé
Aux dés, il est avantageux de parier sur l'apparition d'au moins un \(\textstyle{6}\) au cours de \(\textstyle{4}\) lancers.
Correction
Explication Générale
Le complémentaire de l'événement en question est le fait de n'avoir aucun \(\textstyle{6}\) au cours de \(\textstyle{4}\) lancers, de probabilité \(\textstyle{\left(\frac{5}{6}\right)^4}\) . La probabilité recherchée est donc \(\textstyle{1 - \left(\frac{5}{6}\right)^4> 0,518>\frac{1}{2}}\)
?Question
Énoncé
Aux dés, il est avantageux de parier sur l'apparition d'au moins un double \(\textstyle{6}\) en lançant \(\textstyle{24}\) fois.
Correction
Explication Générale
Le complémentaire de l'événement en question est le fait de n'avoir aucun double \(\textstyle{6}\) au cours de \(\textstyle{24}\) lancers indépendants. La probabilité de cet événement est \(\textstyle{\left(\frac{35}{36}\right)^{24}}\) et donc la probabilité recherchée est \(\textstyle{1- \left(\frac{35}{36}\right)^{24}< 0,49< \frac{1}{2}}\)
?Question
Énoncé
Trois pêcheurs à la ligne attendent que le poisson morde le long d'une rivière. Les probabilités d'attraper un poisson pour chaque pêcheur sont respectivement de \(\textstyle{0,3}\) , \(\textstyle{0,8}\) et \(\textstyle{0,9}\) Quelle est la probabilité qu'il y ait au moins un poisson d'attrapé ?
Correction
Explication Générale
Le complémentaire de l'événement en question est qu'aucun poisson ne soit attrapé. Par indépendance, cet événement est de probabilité égale à \(\textstyle{(1-0,3)(1-0,8)(1-0,9)=0,014}\)
?Question
Énoncé
Soit \(\textstyle{X}\) une variable aléatoire de loi exponentielle de paramètre \(\textstyle{\lambda}\) . La probabilité que \(\textstyle{X}\) se situe entre \(\textstyle{-1}\) et \(\textstyle{5}\)
Correction
Explication Générale
\(\textstyle{\mathbb{P}(-1\leq X\leq 5)= \mathbb{P}(0\leq X\leq 5)= 1- e^{-5\lambda}}\)
?Question
Énoncé
Alice joue au tiercé une fois par semaine. Ayant une bonne connaissance du milieu hippique, elle estime qu'elle a à chaque fois une probabilité \(\textstyle{p=0.1}\) de gagner. Si Alice gagne, elle empoche \(\textstyle{100}\) euros ; dans le cas contraire, elle perd \(\textstyle{10}\)
Correction
?Question
Énoncé
Une urne contient \(\textstyle{7}\) boules blanches et \(\textstyle{10}\) boules noires. On effectue \(\textstyle{n}\) tirages
Correction
?Question
Énoncé
On lance \(\textstyle{10}\) pièces de monnaie de façon indépendante telle que la probabilité de tomber sur pile soit \(\textstyle{0,1}\)
Correction
?Question
Énoncé
Soit \(\textstyle{X}\) suivant une loi binomiale de paramètres \(\textstyle{n}\) et \(\textstyle{p}\) et \(\textstyle{Y}\) suivant une loi binomiale de paramètres \(\textstyle{m}\) et \(\textstyle{p}\) , indépendante de \(\textstyle{X}\) . Alors \(\textstyle{X+Y}\) suit une loi binomiale de paramètres :
Correction
Explication Générale
Une façon simple de le voir : une variable binomiale de paramètre \(\textstyle{n}\) et \(\textstyle{p}\) représente le nombre de succès parmi \(\textstyle{n}\) expériences de Bernoulli indépendantes de probabilité de succès \(\textstyle{p}\)
?Question
Énoncé
Soit \(\textstyle{X}\) une variable normale centrée réduite. Alors \(\textstyle{Y=2X+1}\) suit une loi normale de moyenne \(\textstyle{2}\) et de variance \(\textstyle{1}\)
Correction
Explication Générale
\(\textstyle{Y}\) suit une loi normale de moyenne \(\textstyle{1}\) et de variance \(\textstyle{4}\)
?Question
Énoncé
L'intégrale \(\displaystyle{\int_0^1 e^{2t} dt}\) est égale à
Correction
Explication Générale
Voici des ressources sur les intégrales : Calcul intégral
A voir aussi en vidéo :
?Question
Énoncé
On considère un groupe de 10 personnes, constitué de 4 hommes et 6 femmes. Quel est le nombre d'équipes de deux personnes comprenant un homme et une femme que l'on peut former?
Correction
Explication Générale
Cette ressource peut vous aider : Probabilités et statistiques
?Question
Énoncé
On lance deux dés non pipés. Quelle est la probabilité que la somme des deux dés soit égale à 2 ?
Correction
Explication Générale
Pour approfondir vous pouvez consulter cette ressource Probabilités et statistiques
?Question
Énoncé
Chaque centrale nucléaire a une probabilité de 1/10 d'avoir un accident grave au cours du siècle à venir. Un pays est équipé de 50 centrales. On suppose que les épreuves sont indépendantes (un accident dans une centrale n’entraîne pas un accident dans une autre). La probabilité qu'il y ait au moins un accident grave pendant le siècle prochain est égale à
Correction
Explication Générale
L'événement contraire à "au moins un accident" est "aucun accident".
Pour approfondir vous pouvez consulter cette ressource Probabilités et statistiques
?Question
Énoncé
Soit f la fonction définie par \(f(x)=\frac{\ln(x)}{x^2}\) pour tout x réel strictement positif. La fonction \(f\) vérifie
Correction
Explication Générale
On a \( \lim\limits_{x \to 0+}\ln(x)=-\infty\) et \( \lim\limits_{x \to 0+}\frac{1}{x^2}=+\infty\) d'où \( \lim\limits_{x \to 0+}f(x)=-\infty\). Par ailleurs, \(\ln\) croît "très doucement" devant la fonction carré : \( \lim\limits_{x \to +\infty}f(x)=0\).
Voici une ressource pour revoir quelques notions :
?Question
Énoncé
Soit \(f\) la fonction définie par \( f(t)={\ln(t)-4\over (\ln(t))^2+9}\) pour tout t réel strictement positif.
La fonction \(f\) vérifie
Correction
Explication Générale
En posant \(T=\ln(t)\), on a \( \lim\limits_{t\to0^+} f(t) = \lim\limits_{T\to -\infty} \frac{T-4}{T^2+9} =0\) et \( \lim\limits_{t\to +\infty} f(t) = \lim\limits_{T\to +\infty} \frac{T-4}{T^2+9} =0\).
Voici deux ressources pour revoir quelques notions :
?Question
Énoncé
Soit \(f\) la fonction définie par \(f(x)=\ln\!\left( {x\over x^2+1}\right)\) pour tout \(x\) réel strictement positif. La courbe représentative de la fonction \(f\) a l'allure
Correction
Explication Générale
Déjà, quand \(x\to0^+\), \(\frac{x}{x^2+1}\to 0\) donc \(f(x)\to-\infty\). On peut donc exclure les courbes \((3)\) et \((4)\). En constatant \(f(1)=\ln(1/2)<0\), il ne reste plus que la courbe \((1)\).
Voici deux ressources pour revoir quelques notions :
?Question
Énoncé
Si f est une fonction dérivable sur \( [0,1]\) telle que\( f(0)=0\),\( f(1)=1\) et \(f'\left(\frac12\right)=0\) alors nécessairement
Correction
Explication Générale
?Question
Énoncé
Soit \(f\) la fonction définie par \(f(x)= \frac{x-1}{x^2+3}\) pour tout réel \(x\). La fonction \(f\) vérifie
Correction
Explication Générale
On écrit (pour \(x\neq 0\)) \(f(x)=\frac{x}{x^2}\times\frac{1-1/x}{1+3/x^2}\), soit \(f(x)=\frac{1}{x}\times\frac{1-1/x}{1+3/x^2}\). Quand \(x\;\mathrm{tend\;vers}+\infty\), ou \(x\;\mathrm{tend\;vers}-\infty\), \(1/x\) et \(1/x^2\) tendent vers \(0\), ainsi \(\frac{1-1/x}{1+3/x^2}\to \frac{1-0}{1+0}=1\), et \(\frac{1}{x}\times\frac{1-1/x}{1+3/x^2}\to 0\times 1=0\).
Voici une ressource pour revoir quelques notions :
?Question
Énoncé
La courbe représentative de la fonction \(f:x \mapsto \frac{x-1}{x^2+3}\) a l'allure
Correction
Explication Générale
La fonction \(f\) est continue comme quotient de deux fonctions continues, avec celle au dénominateur ne s'annulant pas. Les courbes \((1)\) et \((2)\) sont donc exclues. On constate que pour \(x<1\), \(f(x)<0\), donc \((4)\) est exclue aussi. Il ne reste que la courbe \((3)\).
Voici une ressource pour revoir quelques notions :
?Question
Énoncé
Si \(f\) est une fonction continue sur \(\mathbb R\) telle que \(f(0)=f(2)=f(4)=1\) et \(f(1)=f(3)=-1\), alors l'équation \(f(x)=0\)
Correction
Explication Générale
Le théorème des valeurs intermédiaires garantit l'existence d'une solution dans \(]0,1[\), d'une dans \(]1,2[\), d'une dans \(]2,3[\) et d'une dans \(]3,4[\). Cela fait quatre solutions positives, mais il y en a peut-être d'autres.
Voici une ressource pour revoir quelques notions :
?Question
Énoncé
Soit f une fonction définie et continue sur un intervalle \(I\) de \(\mathbb{R}\) et \(a \in\ I\). La fonction \(F:I \rightarrow \mathbb{R}\) définie par \(F(x)=\int_a^xf(t){\rm d}t\)
Correction
Explication Générale
Vous pouvez revoir les ressources suivantes :
et en vidéo
Intégrales – Partie 3 : Primitives
Intégrales – Partie 4 : Intégration par parties, changement de variable
?Question
Énoncé
Soient les fonction \(f :x\mapsto\cos(x^2+2)\). La dérivée de \(f\) est
Correction
Explication Générale
Voilà une ressource pour revoir quelques notions essentielles :
?Question
Énoncé
On donne \(f\) la fonction définie sur \(]0;+\infty[\) par \( f(x)=x+1-\frac{\ln x}{x} \) . Sa courbe représentative admet
Correction
Explication Générale
Les limites à considérer sont en \(0\) et \(+\infty\), bien entendu. En \(+\infty\), on se sert de la limite supposée connue de \(\frac{\ln x}{x}\) (zéro) et en \(0\), \(\frac{\ln x}{x}\) tend vers moins l'infini. La limite en \(0\) est infinie et aussi celle en \(+\infty\). Elle admet donc une asymptote verticale, mais pas horizontale !
?Question
Énoncé
Le nombre complexe \(z=(1-2i)^3+(1+2i)^3\) est :
Correction
Explication Générale
Il faut reconnaître la somme de deux nombres complexes conjugués.
?Question
Énoncé
Dans l'industrie automobile, on décide de connaître la proportion de personnes faisant des heures supplémentaires. Pour cela on constitue un échantillon aléatoire et simple de 25 ouvriers et cadres travaillant dans l'industrie automobile. On constate que 10 d'entre eux font des heures supplémentaires. Peut-on donner un intervalle de confiance au niveau de confiance de 95% ?
Correction
Explication Générale
Attention aux conditions d'applications : \(n>30\) Non respectée ici !
Pour approfondir vous pouvez consulter cette ressource Probabilités et statistiques
?Question
Énoncé
On considère la fonction \(f\) définie pour tout \(x>0\) par : \(f(x)=x\ln x +2\)
Correction
Explication Générale
La limite en \(0\) de \(f\) est \(2\). La limite en \(0\) de \(x\ln x\) est \(0\). Par ailleurs par produit, la limite en \(+\infty\) vaut \(+\infty\)
?Question
Énoncé
L'équation d'inconnue complexe \(z\) : \(z^2+z+1=0\) admet :
Correction
Explication Générale
Il suffit juste de connaître la résolution d'une équation du deuxième degré lorsque le discriminant est négatif.
?Question
Énoncé
Déterminer, si elle existe, \(\lim\limits_{x\to 1}\frac{x^2-1}{x-1}\) ?
Correction
Explication Générale
Il s'agit d'une forme indéterminée, pour lever l'indétermination on reconnaît une identité remarquable au numérateur (\(x^2-1=(x-1)(x+1)\))
?Question
Énoncé
Sur un échantillon aléatoire et simple de 100 personnes de la ville de Chombier-Ville, on observe que \(58\) % ont un salaire inférieur ou égal à 2000 euros par mois.On note \(p\) la fréquence des habitants de Chombier-Ville dont le salaire est inférieur ou égal à 2000 euros. L'intervalle de confiance de \(p\) au niveau de confiance de \(95\) % est :
Correction
Explication Générale
Pour approfondir vous pouvez consulter cette ressource Probabilités et statistiques
?Question
Énoncé
Rosette lance une fléchette 15 fois de suite sur une cible circulaire. On admet que les lancers sont indépendants, et que la probabilité pour qu'elle atteigne le centre de la cible sur un lancer est de 0.1. La probabilité qu'elle atteigne au moins une fois le centre dans les 15 tentatives est de :
Correction
Explication Générale
Son événement contraire est "elle n'atteint jamais le centre sur les \(15\) lancers", qui a une probabilité égale à \((0.9)^{15}\)
?Question
Énoncé
Soient \(A\) et \(B\) deux événements d'un univers \(\Omega\). On suppose que \(P(A\cap B)=0.8\) , \(P(A)=0.4\) et \(P(B)=0.2\)
Correction
Explication Générale
Pour approfondir vous pouvez consulter cette ressource Probabilités et statistiques
?Question
Énoncé
La formule de la somme des termes d'une suite arithmétique \((u_n)\) de premier terme \(u_0\) et de raison \(r\in\mathbb{R}\) est :
Correction
Explication Générale
On peut retenir que la somme des termes d'une suite arithmétique est le produit de la moyenne des "extrêmes" par le nombre de termes. En effet,
\(\begin{array}[t]{lccccccccc}2(u_0+u_1+\cdots+u_n)&=&u_0&\quad+&u_1&\quad+&\dots&\quad+&u_n\\ &+&u_n&\quad+&u_{n-1}&\quad+&\dots&\quad+&u_0\\2(u_0+u_1+\cdots+u_n)&=&u_0+u_n&\quad+&u_1+u_{n-1}&\quad+&\dots&\quad+&u_n+u_0\end{array}\)
Comme pour tout \(j\geq 0\), \(u_j=u_0+jr\), on a \(u_j+u_{n-j}=u_0+jr+u_0+(n-j)r=2u_0+nr\). Ainsi
\(\begin{array}[t]{lccccccccc}2(u_0+u_1+\cdots+u_n)&=&2u_0+nr&\quad+&2u_0+nr&\quad+&\dots&\quad+&2u_0+nr\\2(u_0+u_1+\cdots+u_n)&=&(n+1)(2u_0+nr)\end{array}\)
Ce qu'il fallait démontrer.
?Question
Énoncé
Soit \(A\) le point d'affixe \(-8\) et \(B\) le point d'affixe \(4i\) . L'ensemble de tous les points \(M\) d'affixe \(z\) tel que \(|z +8| = |\overline z + 4i|\) est :
Correction
?Question
Énoncé
Soit \(i\) le nombre complexe tel que \(i^2=-1\). Et, pour tout nombre complexe \(z\), notons par \(\overline z\) le conjugué de \(z\).
L'équation \((E) : 2i\overline z =3i + 2iz\)
Correction
Explication Générale
Prenons la forme algébrique de \(z : z=x+iy\)
On obtient : \(\begin{array}{lll} 2i\overline z=3i+2iz & \Leftrightarrow & 2i(x-iy)=3i+2i(x+iy) \\ &\Leftrightarrow & 2y+2ix = -2y+i(2x+3) \\ & \Leftrightarrow & \left\{ \begin{array}{ll} 2y=-2y \\2x=2x+3 \end{array} \right. \end{array}\)
Ce résultat montre que l'équation \((E)\) n'a pas de solution.
?Question
Énoncé
Soit \(i\) le nombre complexe tel que \(i^2=-1\). Et, pour tout nombre complexe \(z\), notons par \(\overline z\) le conjugué de \(z\).
L'équation \((E)\) : \(2i\overline z=3i-2iz\)
Correction
Explication Générale
Prenons la forme algébrique de \(z : z=x+iy\)
On obtient : \(\begin{array}{lll} 2i\overline z=3i+2iz & \Leftrightarrow & 2i(x-iy)=3i-2i(x+iy) \\ &\Leftrightarrow & 2y+2ix = 2y+i(-2x+3) \\ & \Leftrightarrow & 2x=-2x+3 \\ &\Leftrightarrow & x=\frac{3}{4} \end{array}\)
?Question
Énoncé
Soit \(i\) le nombre complexe tel que \(i^2=-1\). Et, pour tout nombre complexe \(z\), notons par \(\overline z\) le conjugué de \(z\).
L'équation \((E) : \frac{\overline z}{z-1} =2\)
Correction
Explication Générale
Prenons la forme algébrique de \(z : z=x+iy\). On obtient :
\(\begin{array}{llllll} \frac{\overline z}{z-1}=2 & \Leftrightarrow & 2\overline z =2(z-1), \;z \ne 1 & \Leftrightarrow& x-iy=2(x-1+iy), & (x ;y)\ne (1 ;0) \\ &\Leftrightarrow & \left\{ \begin{array}{rll} x&=&2(x-1) \\-y&=& 2y \end{array} \right. & \Leftrightarrow& \left\{ \begin{array}{rll} x=2 \\y=0 \end{array} \right. \Leftrightarrow z=2\\ \end{array}\)
?Question
Énoncé
On donne l'intégrale \(I=\displaystyle\int_{-1}^3 |x| dx\).
Coup de pouce
Penser à utiliser la relation de Chasles sur l'intervalle \([-1 ;3]\).
Correction
Explication Générale
Définition
La valeur absolue d'un réel \(x\), notée \(|x|\), est définie par : \(|x|=\left\lbrace\begin{array}{lll} x\quad \mathrm{si} \; x\geq 0 \\ -x \quad \mathrm{si}\; x<0 \end{array}\right.\).
Relation de Chasles
Soit \(f\) une fonction définie et continue sur un intervalle \(I\) de \(\mathbb R\) et soient \(a\),\(b\) et \(c\) trois réels de \(I\). On a l'égalité suivante : \(\displaystyle{\int_a^bf(x)dx=\int_a^cf(x)dx+\int_c^bf(x)dx}\).
Pour déterminer une primitive de \(|x|\) sur \([-1 ;3]\), il faut utiliser l'écriture de \(|x|\) sur \([-1 ;0]\) et sur \([0 ;3]\) et appliquer la relation de Chasles.
\(I=\displaystyle{\int_{-1}^3|x|dx=\int_{-1}^0|x|dx+\int_0^3|x|dx=\int_{-1}^0-xdx+\int_0^3xdx=\left[-\frac{x^2}2\right]^0_{-1}+\left[\frac{x^2}2\right]^3_0=\frac12+\frac92=5}\)
Remarque :
On peut aussi utiliser la représentation graphique de \(|x|\) sur \([-1 ;3]\) et calculer graphiquement l'aire demandée.
Pour ce calcul, on a utilisé la propriété suivante :
Soit \(f\) une fonction définie, continue et positive sur \( [a ; b]\) (avec \(a < b\)).
L'intégrale de \(f\) entre \(a\) et \(b\) est égale à l'aire « sous la courbe » de la fonction \(f\), c'est-à-dire l'aire de la partie du plan délimitée par la courbe de \(f\), l'axe des abscisses et les deux droites d'équation\( x = a\) et \(x = b\).
Cette aire est exprimée en \(u.a.\) (unité d'aire).
?Question
Énoncé
Soit \(f\) une fonction continue sur \(\mathbb R\), soir \(F\) la primitive de \(f\) qui s'annule en \(3\) et \(G\) la primitive de \(f\) qui s'annule en \(0\). L'intégrale \(\int_0^3f(t)dt\)
Correction
Explication Générale
Les deux bonnes réponses sont \(G(3)\) et \(G(x)-F(x)\) pour tout \(x \in \mathbb R\).
Pour faire cet exercice, on utilise le théorème fondamental de l'intégration ainsi que la relation de Chasles pour les intégrales.
En utilisant le théorème fondamental de l'intégration, on peut donner une expression intégrale aux deux fonctions \(F\) et \(G\) : pour tout \(x \in \mathbbs R\), on a \(F(x) =\int_{3}^{x}f(t)dt\; \mathrm{et}\; G(x) =\int_{0}^{x}f(t)dt\).
On en déduit en particulier que :
\(G(3) =\int_{0}^{3}f(t)dt\)
\(F(0) =\int_{3}^{0}f(t)dt = -\int_{0}^{3}f(t)dt\)
pour tout \(x\in\mathbb R\), \(G(x)-F(x) =\int_{0}^{x}f(t)dt-\int_{3}^{x}f(t)dt =\int_{0}^{x}f(t)dt + \int_{x}^{3}f(t)dt =\int_{0}^{3}f(t)dt\) en utilisant la relation de Chasles.
Cela montre que \(F(0)\) est une mauvaise réponse, tandis que \(\int_{0}^{3}f(t)dt\) est bien égale à \(G(3)\) ou à \(G(x)-F(x)\) pour tout \(x\in\mathbb R\).
Enfin, attention à ne pas confondre intégrale et primitive ! Une primitive de \(f\) est une fonction dérivable, dont la dérivée est égale à la fonction \(f\). Ici, \(\int_{0}^{3}f(t)dt\) est l'intégrale de \(f\) sur un segment,
donc est un réel. La réponse "est une primitive de \(f\)" est donc un non-sens.
?Espaces vectoriels
Énoncé
Dans \(\mathbb{R}_3[X]\), l'ensemble des polynômes à coefficients réels de degré \(\le 3\), on considère les polynômes \(P_1= X^3+1, P_2= P'_1 \) (la dérivée de \(P_1\)) et \( P_3 = P''_1\) (la dérivée seconde de \(P_1\)). Quelles sont les assertions vraies ?
Correction
Explication Générale
On vérifie que \(\{P_1,P_2,P_3 \}\) est une famille libre de \(\mathbb{R}_3[X]\) (ce sont des polynômes de degrés distincts). Par contre, elle n'est pas génératrice de \(\mathbfbR}_3[X]\), puisque la dimension de cet espace est \(4\). Le rang d'une famille de vecteurs est la dimension du sous-espace vectoriel engendré par ces vecteurs. Autrement dit, c'est le nombre maximum de vecteurs linéairement indépendants de cette famille.
?Espaces vectoriels
Énoncé
Dans \(\mathbb{R}_3[X]\), l'espace des polynômes à coefficients réels de degré \(\le 3\), on considère les deux sous-espaces vectoriels : \(E= \{P \in \mathbb{R}_3[X] \, ; \; P(0)=P(1)=0\}\; \mbox{ et }\; F= \{(P\in \mathbb{R}_3[X] \, ; \; P'(0)=P''(0)=0 \},\) où \(P'\) (resp. \(P''\)) est la dérivée première (resp. seconde) de \(P\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Une base de \(E\) est \(\{P_1,P_2\}\), où \(P_1=X^3-X\) et \(P_2=X^2-X\), donc \(\dim E=2\). Une base de \(F\) est \(\{Q_1,Q_2\}\), où \(Q_1=1\) et \(Q_2=X^3\), donc \(\dim F=2\). On vérifie que \(E\cap F =\{0\}\). Donc, d'après le théorème de la dimension d'une somme, \(\dim (E+F) = 4\) et comme \(E+F\) est un sous-espace de \(\mathbb{R}_3[X]\) et \(\dim \mathbb{R}_3[X]=4\), \(E+F= \mathbb{R}_3[X]\). Par conséquent, \(E\) et \(F\) sont supplémentaires dans \(\mathbb{R}_3[X]\).
?Applications linéaires
Énoncé
On considère l'application linéaire : \(\begin{array}{rccc}f:&\mathbb{R}_2[X]&\to&\mathbb{R}_2[X]\\& P&\to &XP'-X^2P'' \end{array}\), où \(\mathbb{R}_2[X]\) est l'ensemble des polynômes à coefficients réels de degré \(\le 2\) et \(P'\) (resp. \(P''\)) est la dérivée première (resp. seconde) de \(P\). Quelles sont les assertions vraies ?
Correction
Explication Générale
\(\ker f=\{P \in \mathbb{R}_2[X] \; ; \; XP'-X^2P''=0\}=\{aX^2+b \, ; \; a,b\in \mathbb{R}\}\). Donc \(\{1,X^2\}\) est une base de \(\ker f\). Du théorème du rang, on déduit que \(\mbox{rg}(f)=\dim \textrm{Im} f=1 \) et comme \(f(X)=X\neq 0\), \(\{X\}\) est une base de \(\textrm{Im} f\), donc \(1+X\not\in \textrm{Im}f\). Par conséquent, \(\{1+X\}\) n'est pas une base de \(\textrm{Im} f\).
?Fonctions : domaine de définition (1)
Énoncé
Soient \(f,g\) deux fonctions définies sur \(\mathbb{R}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
La somme et le produit de fonctions est définie partout. Par contre pour le quotient il faut que le dénominateur ne s'annule pas. Pour une racine carrée, il faut que le terme sous la racine soit positif ou nul.
Pour aller plus loin :
cours : Limites et fonctions continues
video : Continuité en un point
video : Notion sur les fonctions
video : La bijection
exercices : Fonctions continues
?Fonctions : domaine de définition (2)
Énoncé
Quelles sont les assertions vraies concernant le domaine de définition des fonctions suivantes ?
Correction
Explication Générale
\(\frac 1x\) est définie pour \(x\neq 0\), \(\sqrt{x}\) est définie pour \(x \ge 0\) ; \(\exp x\) est définie sur \(\mathbb{R}\) ; \(\ln x\) seulement pour \(x > 0\).
Pour aller plus loin :
video : Notion sur les fonctions
?Fonction croissante/décroissante (2)
Énoncé
Quels arguments sont valables pour montrer que \(f : \mathbb{R} \to \mathbb{R}\) est décroissante ?
Correction
Explication Générale
Une fonction \(f\) est décroissante si \(x \le y\) implique \(f(x) \ge f(y)\). Ce qui peut aussi s'écrire \(x \ge y\) qui implique \(f(x) \le f(y)\). Autrement dit \(f\) inverse le sens des inégalités.
Pour aller plus loin :
cours : Limites et fonctions continues
video : Fonctions monotones
?Fonctions : domaine de définition (3)
Énoncé
Soit \(f(x) = \ln(x-1)\) et \(g(x) = \sqrt{x+1}\). Quelles sont les assertions vraies concernant les domaines de définition ? (Rappel : le domaine de définition de \(f\) est le plus grand ensemble \(D_f \subset \mathbb{R}\) sur lequel \(f\) est définie).
Correction
Explication Générale
\(D_f = ]1,+\infty[\) ; \(D_g = [-1,+\infty[\) ; \(D_f \cup D_g = [-1,+\infty[\) ; \(D_{f \times g} = D_f \cap D_g = ]1,+\infty[\) ; \(D_{f \circ g} = ]1,+\infty[\). \(g \circ f\) n'est pas définie pour \(x\) proche de \(1\), en fait \(D_{g\circ f} = [1+\frac1e,+\infty[\).
Pour aller plus loin :
cours : Limites et fonctions continues
video : Notion sur les fonctions
?Fonction croissante/décroissante (4)
Énoncé
Soit \(f : \mathbb{R} \to \mathbb{R}\) une fonction à valeurs strictement positives. Quels arguments sont valables pour montrer que \(f\) est croissante ?
Correction
Explication Générale
En notant \(y = x+h\) avec \(h > 0\) on a \(y > x\) et donc il suffit d'avoir \(\frac{f(y)}{f(x)} \ge 1\). Par contre, il n'est pas suffisant de comparer \(f\) en des valeurs distantes de \(1\) ! Essayez de dessiner un contre-exemple : \(f\) vaut \(0\) partout, sauf \(1\) en chaque entier.
Pour aller plus loin :
cours : Limites et fonctions continues
video : Fonctions monotones
?Fonctions - zéros de fonction (1)
Énoncé
Quelles assertions peut-on déduire du théorème des valeurs intermédiaires ?
Correction
Explication Générale
Pour montrer qu'une fonction \(f\) continue sur un intervalle \([a,b]\) s'annule sur cet intervalle, il est suffisant de montrer que le produit \(f(a)\times f(b) <0 \). Ce qui correspond à la situation où la fonction change de signe sur l'intervalle.
Pour aller plus loin :
cours : Limites et fonctions continues
video : Continuité en un point
video : Notion sur les fonctions
exercices : Fonctions continues
?Fonctions - zéros de fonction (2)
Énoncé
Soit \(f(x)=x^2-7\). On calcule \(f(2,125)=-1,9375\) ; \(f(2,5) = -0,75\) ; \(f(2,625) = -0,109375\) ; \(f(2,75) = 0,5625\). Quelles sont les assertions vraies ?
Correction
Explication Générale
La fonction \(f\) est continue et s'annule en \(\sqrt{7}\). Comme \(f(2,625) < 0\) et \(f(2,75) > 0\), alors \(2,625 < \sqrt{7} < 2,75\).
Pour aller plus loin :
cours : Limites et fonctions continues
video : Continuité en un point
exercices : Fonctions continues
?Fonctions - zéros de fonction (3)
Énoncé
Soit \(f : [a,b] \to \mathbb{R}\) une fonction continue (avec \(a < b\)). Quelles assertions sont une conséquence du théorème des valeurs intermédiaires ?
Correction
Explication Générale
Citons ici trois conséquences du théorème des valeurs intermédiaires :
pour \(f : [a,b] \to \mathbb{R}\) continue,
(1) si \(f(a) \cdot f(b) \le 0\) alors \(f\) s'annule sur \([a,b]\) ;
(2) si \(f(a) < k < f(b)\) alors il existe \(a < c < b\) tel que \(f(c)=k\) ;
(3) si \(I\) est un intervalle, alors \(f(I)\) est un intervalle.
Pour aller plus loin :
cours : Limites et fonctions continues
video : Continuité en un point
video : Notion sur les fonctions
exercices : Fonctions continues
?Fonctions : maximum/minimum (2)
Énoncé
Soit \(f(x) = x \sin(\pi x) - \ln(x) - 1\) définie sur \(]0,1]\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Attention l'intervalle de définition n'est pas fermé borné. Par contre la limite de \(f\) en \(0\) en \(+\infty\) et \(f(1) = -1\). On en déduit que \(f\) n'est pas majorée, par contre elle est minorée, et par le théorème des valeurs intermédiaires, elle s'annule.
Pour aller plus loin :
cours : Limites et fonctions continues
video : Extremum d'une fonction
exercices : Fonctions continues
?Fonctions : maximum/minimum (3)
Énoncé
Soit \(I\) un intervalle de \(\mathbf{R}\) et soit \(f : I \to \mathbf{R}\) une fonction continue. Soit \(J=f(I)\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Par une fonction continue, l'image d'un intervalle est un intervalle ; l'image d'un intervalle fermé et borné est un intervalle fermé et borné.
Pour aller plus loin :
cours : Limites et fonctions continues
video : Extremum d'une fonction
exercices : Fonctions continues
?Dérivée seconde ou plus (2)
Énoncé
Soit \(x\in\mathbb R\), soit \(\displaystyle f(x)=x^2\mathrm{e}^x\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On applique la formule de Leibniz \(\displaystyle f^{(n)}(x)=\sum _{k=0}^n\mathrm{C}_n^k(x^2)^{(k)}(\mathrm{e}^x)^{(n-k)}=[x^2+2nx+n(n-1)]\mathrm{e}^x.\)
?Dérivée seconde ou plus (3)
Énoncé
Soit \(n\) un entier naturel non nul, soit \(x \in ]-1 , +\infty[\) et soit \(\displaystyle f(x)=x\ln (1+x)\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On peut, par exemple, appliquer la formule de Leibniz \(\displaystyle f^{(n)}(x)=\sum _{k=0}^n\mathrm{C}_n^k(x)^{(k)}(\ln (1+x))^{(n-k)}.\) Mais \(\displaystyle \left[\ln (1+x)\right]^{(k)}=\frac{(-1)^{k-1}(k-1)!}{(1+x)^k}\). Ce qui donne \(f^{(n)}(x)=\frac{(-1)^{n}(n-2)!}{(1+x)^n}\left(x+n\right).\)
?Dérivée seconde ou plus (4)
Énoncé
Soit \(f(x)=\left\{\begin{array}{ll}x^2\ln (x^2)&\mbox{si }x\neq 0\\ 0&\mbox{si }x=0.\end{array} \right.\) Quelles sont les bonnes réponses ?
Correction
Explication Générale
Les théorèmes généraux assurent que \(f\) est de classe \(\mathcal{C}^2\) sur \(\mathbf{R}^*\) avec \(f'(x)=2x\ln (x^2)+2x\mbox{ et }f''(x)=2\ln x^2+6\mbox{ si }x\neq 0\) et \(\displaystyle \lim _{x\to 0}\frac{f(x)-f(0)}{x-0}=0=f'(0)\). On a aussi \(\lim _{x\to 0}f'(x)=0=f'(0) \Rightarrow f'\mbox{ est continue en }0.\) Ainsi \(f\) de classe \(\mathcal{C}^1\) sur \(\mathbf{R}\) et est deux fois dérivable sur \(\mathbf{R}^*\). Elle n'est pas deux fois dérivables en \(0\) car \(\lim _{x\to 0}\frac{f'(x)-f'(0)}{x-0}=\lim _{x\to 0}[2\ln (x^2)+2]=-\infty.\)
Pour aller plus loin :
cours : Dérivée d'une fonction
video : Définition de la dérivée
video : Calculs dérivées usuelles
?Développements limités
Énoncé
Soit \(\displaystyle f(x)=\frac{\ln (1+x+x^2)}{\sqrt{1+2x}-1}\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Pour écrire le \(DL_2(0)f(x)\), il faut écrire les développements limités du numérateur et du dénominateur à l'ordre \(3\) en \(0\). Ensuite effectuer la division suivant les puissances croissantes à l'ordre \(2\). On aura : \(DL_2(0)f(x)=1+x-\frac{2x^2}{3}+o(x^2)\). En multipliant par \(x\), on obtient : \(\displaystyle DL_3(0)xf(x)=x+x^2-\frac{2x^3}{3}+o(x^3)\).
?Développements limités
Énoncé
Parmi les assertions suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
La division suivant les puissances croissantes du \(\displaystyle DL_3(0)\ln (1+x)\) par \(x-x^2\) donne \(DL_2(0)\frac{\ln (1+x)}{x-x^2}=1+\frac{x}{2}+\frac{5x^2}{6}+o(x^2)\). La division suivant les puissances croissantes du \(\displaystyle DL_3(0)(\mathrm{e}^x-1)\) par le \(\displaystyle DL_3(0)\ln (1+x)\) donne \(DL_2(0)\frac{\mathrm{e}^x-1}{\ln (1+x)}=1+x+\frac{x^2}{3}+o(x^2)\). Ensuite, avec \(\displaystyle u=x\sin x =x^2-\frac{x^4}{6}+o(x^4)\) et \(\ln (1+u)=u-u^2/2+o(u^2)\), on obtient : \(DL_4(0)\ln (1+x\sin x)=x^2-\frac{2x^4}{3}+o(x^4)\). Enfin, avec \(\displaystyle u=\ln (1+x^2)=x^2-\frac{x^4}{2}+o(x^4)\) et \(\arcsin u=u+\frac{u^3}{6}+o(u^4)\), on obtient : \(DL_4(0)\arcsin \left(\ln (1+x^2)\right)=x^2-\frac{x^4}{2}+o(x^4)\).
?Développements limités
Énoncé
Soit \(f\) telle que \(\displaystyle f(x)=\frac{\mathrm{e}^{x}-1}{x+x^2}\) si \(x\neq 0\) et \(f(0)=1\). On note \(T_0\) la tangente au graphe de \(f\) au point d'abscisse \(0\) lorsqu'elle existe. Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Pour écrire le \(DL_2(0)f(x)\), on utilise le \(DL_3(0)(\mathrm{e}^{x}-1)\). La division suivant les puissances croissantes donne : \(\displaystyle DL_2(0)f(x)=1-\frac{x}{2}+\frac{2x^2}{3}+o(x^2)\). Ainsi \(\displaystyle \lim _{x\to 0}f(x)=1\) et \(f\) est continue en \(0\) et, puisque \(f\) admet un \(DL_1(0)\), \(f\) est dérivable en \(0\). De plus, \(T_0\) est la droite d'équation \(\displaystyle y=1-\frac{x}{2}\) et puisque \(\displaystyle f(x)-y=\frac{2x^2}{3}+o(x^2)\geq 0\) au voisinage de \(0\) : le graphe de \(f\) est au dessus de \(T_0\) au voisinage de \(0\).
?Développements limités
Énoncé
Soit \(\displaystyle f(x)=\sqrt{2+x^2}\). On note \(\Gamma\) le graphe de \(f\) et on pose \(\displaystyle g(x)=xf\left(\frac{1}{x}\right)\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
D'abord, au voisinage de \(0^+\), on a : \(g(x)=\sqrt{1+2x^2}=1+x^2+o(x^2)\) et donc, au voisinage de \(+\infty\), on a : \(f(x)=x+\frac{1}{x}+o\left(\frac{1}{x}\right)\mbox{ car }f(x)=xg\left(\frac{1}{x}\right)\). La droite d'équation \(y=x\) est une asymptote au voisinage de \(+\infty\). De plus, au voisinage de \(+\infty\), \(\displaystyle f(x)-y=\frac{1}{x}+o\left(\frac{1}{x}\right)\geq 0\). Donc \(\Gamma\) est au dessus de la droite d'équation \(y=x\) au voisinage de \(+\infty\).
?Développements limités
Énoncé
Soit \(f\) telle que \(\displaystyle f(x)=\frac{\mathrm{e}^{2x}-1}{x^2+2\sin x}\) si \(x\neq 0\) et \(f(0)=1\). On note \(T_0\) la tangente au graphe de \(f\) au point d'abscisse \(0\) lorsqu'elle existe. Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Pour écrire le \(DL_2(0)f(x)\), on utilise le \(DL_3(0)(\mathrm{e}^{2x}-1)\) et le \(DL_3(0)(x^2+2\sin x)\). La division suivant les puissances croissantes donne : \(\displaystyle DL_2(0)f(x)=1+\frac{x}{2}+\frac{7x^2}{12}+o(x^2)\). Ainsi \(\displaystyle \lim _{x\to 0}f(x)=1\) et \(f\) est continue en \(0\) et, puisque \(f\) admet un \(DL_1(0)\), \(f\) est dérivable en \(0\). De plus, \(T_0\) est la droite d'équation \(\displaystyle y=1+\frac{x}{2}\) et puisque \(\displaystyle f(x)-y=\frac{7x^2}{12}+o(x^2)\geq 0\) au voisinage de \(0\) : le graphe de \(f\) est au dessus de \(T_0\) au voisinage de \(0\).
?Développements limités
Énoncé
On considère les fonctions \(f\) et \(g\) telles que \(\displaystyle f(x)=(1+x)\mathrm{e}^{1/(x+1)}\) et \(\displaystyle g(x)=xf\left(\frac{1}{x}\right)\). On note \(\Gamma\) le graphe de \(f\) et \(\Delta\) la droite d'équation \(\displaystyle y=x+2\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
On a : \(\displaystyle g(x)=(1+x)\mathrm{e}^{x/(1+x)}\). Dans \(\displaystyle \mathrm{e}^u=1+u+\frac{u^2}{2}+o(u^2)\), on pose \(\displaystyle u=\frac{x}{1+x}=x-x^2+o(x^2)\). Ceci donne : \(DL_2(0)g(x)=1+2x+\frac{x^2}{2}+o(x^2)\Rightarrow DL_1(+\infty)f(x)=x+2+\frac{1}{2x}+o\left(\frac{1}{x}\right)\). Ainsi, au voisinage de \(+\infty\), \(\Gamma\) admet \(\Delta\) comme asymptote et \(\Gamma\) est situé au dessus de \(\Delta\) car \(\displaystyle f(x)-y=\frac{1}{2x}+o\left(\frac{1}{x}\right)\geq 0\) au voisinage de \(+\infty\). Au voisinage de \(-\infty\), \(\Gamma\) est situé en dessous de \(\Delta\) car \(\displaystyle f(x)-y=\frac{1}{2x}+o\left(\frac{1}{x}\right)\leq 0\) au voisinage de \(-\infty\).
?Équations différentielles du second ordre
Énoncé
On considère les équations différentielles : \((E_1)\; :\; y''-y=3+\mathrm{e}^{2x}\quad \mbox{et}\quad (E_2)\; :\; y''-y=2+\mathrm{e}^{x}\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Les solutions de l'équation caractéristique associée à \((E_1)\) sont \(\pm 1\). Donc \((E_1)\) admet une solution particulière sous la forme \(\displaystyle y_0=a+b\mathrm{e}^{2x}\), car \(2\) n'est pas une racine de l'équation caractéristique, et \((E_2)\) admet une solution particulière sous la forme \(\displaystyle y_0=a+bx\mathrm{e}^{x}\) car \(1\) est une racine simple de l'équation caractéristique. La solution générale de \((E_1)\) est : \(\displaystyle y=-3+\frac{\mathrm{e}^{2x}}{3}+k_1\mathrm{e}^{x}+k_2\mathrm{e}^{-x}\), \(k_1,k_2\in \mathbb{R}\).
?Équations différentielles du second ordre
Énoncé
On considère les équations différentielles : \((E_1)\; :\; y''-4y'+4y=4+2\mathrm{e}^{2x}\quad \mbox{et}\quad (E_2)\; :\; y''-4y'+4y=8+\mathrm{e}^{x}\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
L'équation caractéristique associée à \((E_1)\) admet \(2\) comme racine double. Donc \((E_1)\) admet une solution particulière sous la forme \(\displaystyle y_0=(a+bx+cx^2)\mathrm{e}^{2x}\), car \(2\) est une racine double de l'équation caractéristique, et \((E_2)\) admet une solution particulière sous la forme \(\displaystyle y_0=a+b\mathrm{e}^{x}\) car \(1\) n'est pas une racine de l'équation caractéristique. La solution générale de \((E_2)\) est \(\displaystyle y=2+\mathrm{e}^{x}+\left(k_1+k_2x\right)\mathrm{e}^{2x}\), \(k_1,k_2\in \mathbb{R}\).
?Équations différentielles du second ordre
Énoncé
On considère les équations différentielles : \((E_1)\; :\; y''-3y'+2y=\mathrm{e}^{2x}\quad \mbox{et}\quad (E_2)\; :\; y''-3y'+2y=2x\mathrm{e}^{x}\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Les racines de l'équation caractéristique associée à \((E_1)\) sont \(1\) et \(2\). Donc \((E_1)\) admet une solution particulière sous la forme \(\displaystyle y_0=ax\mathrm{e}^{2x}\), car \(2\) est une racine simple de l'équation caractéristique, et \((E_2)\) admet une solution particulière sous la forme \(\displaystyle y_0=x(a+bx)\mathrm{e}^{x}\) car \(1\) est une racine simple de l'équation caractéristique associée à \((E_2)\).
?Équations différentielles du second ordre
Énoncé
On considère les équations différentielles : \((E_1)\; :\; y''-4y'+5y=\mathrm{e}^{2x}\quad \mbox{et}\quad (E_2)\; :\; y''-4y'+5y=8\sin x\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Les solutions de l'équation caractéristique sont \(2\pm \mathrm{i}\). Donc \((E_1)\) admet une solution particulière sous la forme \(\displaystyle y_0=a\mathrm{e}^{2x}\) et \((E_2)\) admet une solution particulière sous la forme \(\displaystyle y_0=a\cos x+b\sin x\). Les calculs montrent que la solution générale de \((E_1)\) est \(\displaystyle y=\mathrm{e}^{2x}\left[1+a\cos x+b\sin x\right]\), \(a,b\in \mathbb{R}\), et la solution générale de \((E_2)\) est : \(y=\left(1+a\mathrm{e}^{2x}\right)\cos x+\left(1+b\mathrm{e}^{2x}\right)\sin x,\; a,b\in \mathbb{R}\).
?Polynômes - transformation
Énoncé
Soit \(P(X) = X^n + a_{n-1}X^{n-1} + \cdots + a_1X+a_0\) un polynôme de \(\mathbf{R}[X]\) de degré \(n \ge 1\). À cette fonction polynôme \(P\) on associe une nouvelle fonction polynôme \(Q\), défini par \(Q(X) = P(X - \frac{a_{n-1}}{n})\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Cette transformation est faite afin que le coefficient du monôme \(X^{n-1}\) de \(Q\) soit toujours nul.
Pour aller plus loin :
cours : Polynômes
video : Définitions
?Fonctions usuelles - Domaine de définition (1)
Énoncé
Soit \(f(x)= \frac{x^2+3x+2}{x^2-2x-1}\) et \( g(x)= \sqrt{x^2-1}\). On notera \(D_f\) et \(D_g\) le domaine de définition de \(f\) et de \(g\) respectivement. Quelles sont les assertions vraies ?
Correction
Explication Générale
\(f\) est définie si et seulement si \(x^2-2x-1 \neq 0\), c'est-à-dire \(x\neq 1-\sqrt 2\) et \(x\neq 1+\sqrt 2\). \(g\) est définie si et seulement si \(x^2-1 \ge 0\), c'est-à-dire \(x\ge 1\) ou \(x\le -1\).
Pour aller plus loin :
video : Notion sur les fonctions
?Fonctions usuelles - Domaine de définition (3)
Énoncé
Soit \( f(x)= \ln(\frac{2+x}{2-x}) \) et \(g(x)=x^x\). On notera \(D_f\) et \(D_g\) le domaine de définition des fonctions \(f\) et \(g\) respectivement. Quelles sont les assertions vraies ?
Correction
Explication Générale
\(f\) est définie si \(x\neq 2\) et \(\frac{2+x}{2-x}\ge 0\). On déduit que \(D_f=]-2,2[\). Par définition, \(g(x)=e^{x\ln x}\). Donc \(g\) est définie si \(x > 0\).
Pour aller plus loin :
video : Notion sur les fonctions
video : Logarithme Népérien
video : Exponentielle
?Fonctions usuelles - Domaine de définition (4)
Énoncé
Soit \(f(x)= \arcsin (2x), \, g(x)= \arccos (x^2-1) \) et \(h(x)= \arctan \sqrt{x}\). On notera \(D_f,D_g\) et \(D_h\) le domaine de définition de \(f, g\) et \(h\) respectivement. Quelles sont les assertions vraies ?
Correction
Explication Générale
Les fonctions \(x\mapsto \arcsin x\) et \(x \mapsto \arccos x\) sont définies sur \([-1,1]\) et la fonction \(x \mapsto \arctan x\) est définie sur \(\mathbf{R}\). On déduit que : \(f\) est définie si \(-1\le 2x\le 1\), c'est-à-dire \(x \in [-\frac{1}{2}, \frac{1}{2}]\), \(g\) est définie si \(-1 \le x^2-1 \le 1\), c'est-à-dire \(x\in [-\sqrt 2, \sqrt 2]\) et \(h\) est définie si \(x\ge 0\).
Pour aller plus loin :
video : Fonctions circulaires inverses
?Fonctions usuelles - logarithme
Énoncé
Soit \((E)\) l'équation : \(\ln (x^2-1) = \ln (x-1) + \ln 2\). Quelles sont les assertions vraies ?
Correction
Explication Générale
\((E)\) est définie si \(x^2-1 > 0\) et \(x-1 > 0\), c'est-à-dire \(x > 1\). Soit \(x > 1\), alors \((E) \Leftrightarrow \ln (x-1) + \ln (x+1)= \ln (x-1) + \ln 2 \Leftrightarrow \ln (x+1)= \ln 2 \Leftrightarrow x=1,\) ce qui n'est pas compatible.
Pour aller plus loin :
video : Logarithme Népérien
?Fonctions usuelles - exponentielle
Énoncé
Soit \((E)\) l'équation : \(e^{2x}+e^x-2=0\). Quelles sont les assertions vraies ?
Correction
Explication Générale
La fonction exponentielle est définie sur \(\mathbf{R}\), donc \((E)\) est définie sur \(\mathbf{R}\). En posant \(y=e^x\), on se ramène à résoudre l'équation du second degré \(y^2+y-2=0\). En résolvant cette équation, on obtient \(y=1\) ou \(y=-2\). L'équation \(e^x = -2\) n'ayant pas de solution, on trouve \(x=0.\) Par conséquent, \(x=0\).
Pour aller plus loin :
video : Exponentielle
?Fonctions usuelles - étude de fonction (1)
Énoncé
Soit \(f(x)=\sqrt[3]{1-x^3}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
La fonction \(x\to \sqrt[3]{x}\) est définie sur \(\mathbf{R}\), elle est continue, strictement croissante et établit une bijection de \(\mathbf{R}\) dans \(\mathbf{R}\). On déduit que \(f\) est définie sur \(\mathbf{R}\), elle est strictement décroissante et établit une bijection de \(\mathbf{R}\) dans \(\mathbf{R}\). Soit \(y\in \mathbf{R}\), on a : \(y=\sqrt[3]{1-x^3} \Leftrightarrow 1-x^3=y^3 \Leftrightarrow x=\sqrt[3]{1-y^3}\). Donc l'application réciproque de \(f\) est \(f\).
Pour aller plus loin :
video : Fonctions monotones
video : La bijection
?Fonctions usuelles - domaine de définition (5)
Énoncé
Soit \(f(x)= \sqrt[3]{1-x^2}\) et \( g(x)= e^{\frac{1}{x}}\sqrt[4]{1-|x|} \). On notera \(D_f\) et \(D_g\) le domaine de définition de \(f\) et \(g\) respectivement. Quelles sont les assertions vraies ?
Correction
Explication Générale
la fonction \(x\to \sqrt[3]{x}\) est définie sur \(\mathbf{R}\), donc \(D_f=\mathbf{R}\). La fonction \(x\mapsto \sqrt[4]{x}\) est définie sur \([0,+\infty[\). On déduit que \(D_g=[-1,0[\cup ]0,1]\).
Pour aller plus loin :
cours : Fonctions usuelles
video : Notion sur les fonctions
video : Exponentielle
?Fonctions usuelles - étude de fonction (3)
Énoncé
Soit \(f(x)=\arcsin x + \arccos x\). Quelles sont les assertions vraies ?
Correction
Explication Générale
\(f\) est définie sur \([-1,1]\), dérivable sur \(]-1,1[\) et \(f'(x)=0\), \(\forall x \in ]-1,1[\). Puisque \(]-1,1[\) est un intervalle, on déduit que \(f\) est constante sur \(]-1,1[\) et comme \(f\) est continue sur \([-1,1]\), \(f\) est constante sur \([-1,1]\). Or \(f(0)=\frac{\pi}{2}\), donc \(f(x)=\frac{\pi}{2}, \, \forall x \in [-1,1]\).
Pour aller plus loin :
video : Fonctions circulaires inverses
exercices : Fonctions circulaires et hyperboliques inverses
?Courbes parametrées
Énoncé
La trajectoire \(\Gamma\) d'une particule en mouvement est donnée par les équations \(x=2+\cos t\quad \mbox{et} \quad y=\frac{t^2}{2}+\sin t\).
Correction
Explication Générale
Notons \(f(t)=(x(t),y(t))\). Le système \(f'(t)=(0,0)\) n'admet pas de solution, donc \(\Gamma\) n'admet pas de point stationnaire. \(\displaystyle \lim _{t\to \pm\infty}x(t)\) n'existe pas. Un DL de \(f\) en \(\pi/2\), \(f(t)=\binom{2}{1+\pi^2/8}+(t-\frac{\pi}{2})\binom{-1}{\pi/2}+(t-\frac{\pi}{2})^3\binom{1/6}{0}+(t-\frac{\pi}{2})^3\binom{\varepsilon_1(t)}{\varepsilon_2(t)}\mbox{ avec }\lim _{t\to 0}\varepsilon_i(t)=0\), montre que le point de paramètre \(t=\pi/2\) est un point d'inflexion et la tangente en ce point est dirigée par le vecteur \(f'(\pi/2)=(-1,\pi/2)\). Enfin \(y\) n'est ni paire ni impaire, donc \(\Gamma\) n'est pas symétrique par rapport à l'axe des \(x\).
?Intégration par parties
Énoncé
On note par \(F\) une primitive de \(f(x)=\arcsin (x)\) sur \(]-1,1[\). Parmi les propositions suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Une intégration par parties avec \(u=\arcsin (x)\) et \(v=x\) donne \(F(x)=x\arcsin (x)-\int \frac{x\mathrm{d}x}{\sqrt{1-x^2}}=x\arcsin (x)+\sqrt{1-x^2}+k,\; k\in \mathbb{R}\).
?Intégration par parties
Énoncé
On note par \(F\) une primitive de \(f(x)=\arctan (x)\) sur \(\mathbb{R}\). Parmi les propositions suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Une intégration par parties avec \(u=\arctan (x)\) et \(v=x\) donne \(\int \arctan (x)\mathrm{d}x=x\arctan (x)-\int \frac{x\mathrm{d}x}{1+x^2}=x\arctan (x)-\frac{1}{2}\ln (1+x^2)+k,\; k\in \mathbb{R}\).
?Intégration par parties
Énoncé
On se place sur \(]-1,+\infty[\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Une intégration par parties avec \(u=\ln (x+1)\) et \(v=x+1\) donne \(\int \ln (x+1)\, \mathrm{d}x=(x+1)\ln (x+1)-\int \mathrm{d}x=(x+1)\ln (x+1)-x+k,\; k\in \mathbb{R}\). Une intégration par parties avec \(u=\ln (x+1)\) et \(v=x^2/2\) donne \(\int x\ln (1+x)\mathrm{d}x=\frac{x^2}{2}\ln (1+x)-\int \frac{x^2\mathrm{d}x}{2(1+x)}\).
?Intégrale définie
Énoncé
Parmi les égalités suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Une intégration par parties, avec \(u=x\) et \(v=-\cos x\Rightarrow v'=\sin x\), donne \(\int _0^{\pi}x\sin x\,\mathrm{d}x=\Big[-x\cos x\Big]_0^{\pi}+\int _0^{\pi}\cos x\mathrm{d}x=\pi +\int _0^{\pi}\cos x\mathrm{d}x=\pi\).
?Intégrale définie
Énoncé
Parmi les égalités suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Une intégration par parties, avec \(u=x\) et \(v=\sin x\Rightarrow v'=\cos x\), donne \(\int _0^{\pi}x\cos x\,\mathrm{d}x=\Big[x\sin x\Big]_0^{\pi}-\int _0^{\pi}\sin x\mathrm{d}x=-\int _0^{\pi}\sin x\mathrm{d}x=\Big[\cos x\Big]_0^{\pi}=-2\).
?Intégrale définie
Énoncé
Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Une intégration par parties avec \(u=\ln t\) et \(v=t\Rightarrow v'=1\) donne : \(\displaystyle \int _1^{\mathrm{e}}\ln t\mathrm{d}t=\Big[t\ln t\Big]_1^{\mathrm{e}}-\int _1^{\mathrm{e}}\mathrm{d}t=1\). Une intégration par parties, avec \(u=\ln t\) et \(v=t^2/2\Rightarrow v'=t\), donne : \(\displaystyle \int _1^{2}t\ln t\mathrm{d}t=\left[\frac{t^2}{2}\ln t\right]_1^{2}-\int _1^{2}\frac{t}{2}\mathrm{d}t=2\ln 2-\frac{3}{4}\).
?Intégrale définie
Énoncé
Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Une intégration par parties avec \(u=x\) et \(v=\mathrm{e}^x\Rightarrow v'=\mathrm{e}^x\) donne : \(\int _0^1x\mathrm{e}^x\, \mathrm{d}x=\Big[x\mathrm{e}^x\Big]_0^1-\int _0^1\mathrm{e}^x\, \mathrm{d}x=1\). Une intégration par parties avec \(u=x^2\) et \(v=\mathrm{e}^x\Rightarrow v'=\mathrm{e}^x\) donne : \(\int _0^1x^2\mathrm{e}^x\, \mathrm{d}x=\Big[x^2\mathrm{e}^x\Big]_0^1-2\int _0^1x\mathrm{e}^x\, \mathrm{d}x=\mathrm{e}-2\).
?Intégrale définie
Énoncé
On note \(\displaystyle I=\int _{0}^{2}x^2\ln (x+1)\, \mathrm{d}x\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Pour tout \(x\in ]0,2[\), \(x^2\ln (x+1) < 4\ln (x+1)\) et \(x^2\ln (x+1) < x^2\ln 3\). Donc \(\displaystyle I < 4\int _{0}^{2}\ln (x+1)\, \mathrm{d}x\) et \(\displaystyle I < \ln 3\int _{0}^{2}x^2\, \mathrm{d}x\). Enfin, une intégration par parties avec \(u=\ln (x+1)\) et \(v=x^3/3\) donne : \(I=\frac{8}{3}\ln 3-\frac{1}{3}\int _{0}^{2}\frac{x^3\, \mathrm{d}x}{x+1}=3\ln 3-\frac{8}{9}\).
?Intégrale définie
Énoncé
On pose \(\displaystyle I=\int _0^{\pi/2}x\cos ^2x\, \mathrm{d}x\), \(\displaystyle J=\int _0^{\pi/2}x\sin ^2x\, \mathrm{d}x\) et \(\displaystyle K=\int _0^{\pi/2}x\cos (2x)\, \mathrm{d}x\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Une intégration par parties, avec \(u=x\) et \(v=1/2\sin (2x)\), donne \(K=\left[\frac{x}{2}\sin (2x)\right]_0^{\pi/2}-\frac{1}{2}\int _0^{\pi/2} \sin (2x)\, \mathrm{d}x=-\frac{1}{2}\). A l'aide des relations \(\cos ^2x+\sin ^2x=1\) et \(\cos ^2x-\sin ^2x=\cos (2x)\), on obtient : \(I+J=\int _0^{\pi/2}x\mathrm{d}x=\frac{\pi ^2}{8}\mbox{ et }I-J=K=-\frac{1}{2}\). La somme et la différence de ces égalités donnent : \(\displaystyle I=\frac{\pi ^2-4}{16}\) et \(\displaystyle J=\frac{\pi ^2+4}{16}\).
?Limites des fonctions réelles
Énoncé
Soit \(f(x)= \frac{\sqrt {x+1}-\sqrt {2x}}{x-1}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
On multiplie le numérateur et le dénominateur de \(f\) par l'expression conjuguée de \(\sqrt {x+1}-\sqrt {2x}\), c'est-à-dire par \(\sqrt {x+1}+\sqrt {2x}\). On obtient : \(f(x)= -\frac{1}{\sqrt {x+1}+\sqrt {2x}}\).
Pour aller plus loin :
exercices : Limites de fonctions
?Limites des fonctions réelles
Énoncé
Soit \(f(x)= x\ln x -x^2+1\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Si \(\alpha\) et \( \beta\) sont des réels \( > 0\), alors en \(+\infty\), on a : \((\ln x)^{\alpha} \ll x^{\beta}\), où la notation \(f\ll g\) signifie : \(\lim_{x \to + \infty} \frac{f(x)}{g(x)}=0. \) On a aussi \(\lim_{x\to 0^+} x^{\beta} |\ln x|^{\alpha} = 0\).
Pour aller plus loin :
video : Logarithme Népérien
?Limites des fonctions réelles - limite en l'infini (2)
Énoncé
Soit \(f(x)= e^{2x}-x^7+x^2-1\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Si \(\alpha\) et \( \beta\) sont des réels \( > 0\), alors en \(+\infty\), on a : \( x^{\alpha}\ll e^{\beta x}\), où la notation \(f\ll g\) signifie : \(\lim_{x \to + \infty} \frac{f(x)}{g(x)}=0 \).
Pour aller plus loin :
video : Exponentielle
?Limites des fonctions réelles - limite en un point
Énoncé
Soit \(f(x)= \frac{\cos x-1}{x^2}\). Quelles sont les assertions (ou propositions) vraies ?
Correction
Explication Générale
On a : \(\cos x = \cos^2 (\frac{x}{2}) - \sin^2 (\frac{x}{2})\) et \(1= \cos^2 (\frac{x}{2}) + \sin^2 (\frac{x}{2})\), donc \(\cos x - 1 = -2 \sin ^2 (\frac{x}{2})\). D'autre part, \(\lim_{x\to 0}\frac{\sin x}{x} = 1\). On déduit que \(\lim_{x\to 0} f(x) = \lim_{x\to 0} -\frac{1}{2} \big(\frac{\sin (\frac{x}{2})}{\frac{x}{2}}\big)^2 = -\frac{1}{2}\).
Pour aller plus loin :
video : La fonction cosinus
?Nombres complexes - écriture algébrique
Énoncé
Soit \(z=(1-2i)^2\). Quelles sont les assertions vraies ?
Correction
Explication Générale
On développe \((1-2i)^2\). Si \(z=a+ib, a,b \in \mathbf{R}, \overline{z}=a-ib\) et \(|z|^2= a^2+b^2\).
Pour aller plus loin :
cours : Nombres complexes
?Nombres complexes - écriture algébrique
Énoncé
Soit \(z=\frac{i+1}{1-i\sqrt 3}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
On applique les formules : \(|\frac{z_1}{z_2}|= \frac{|z_1|}{|z_2|}\), \(|z|^2=z\overline{z}\) et \(\arg(\frac{z_1}{z_2})= \arg z_1 - \arg z_2 \, [2\pi]\).
Pour aller plus loin :
cours : Nombres complexes
video : Conjugué d'un nombre complexe
video : Module d'un nombre complexe
?Nombres complexes - écriture algébrique
Énoncé
Soit \(z\) un nombre complexe de module \(2\) et d'argument \(\frac{\pi}{4}\). L'écriture algébrique de \(z\) est :
Correction
Explication Générale
\(z=2(\cos\frac{\pi}{4}+i\sin\frac{\pi}{4}) =\sqrt 2+i\sqrt 2 \).
Pour aller plus loin :
cours : Nombres complexes
video : Module d'un nombre complexe
video : Argument d'un nombre complexe
?Nombres complexes - module/argument
Énoncé
Soit \(z=\frac{(1-i)^{10}}{(1+i\sqrt 3)^4}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
On applique les formules : \(|\frac{z_1^n}{z_2^m}|= \frac{|z_1|^n}{|z_2|^m}\) et \(\arg(\frac{z_1^n}{z_2^m})= n\arg z_1 - m\arg z_2 \, [2\pi]\).
Pour aller plus loin :
video : Module d'un nombre complexe
video : Argument d'un nombre complexe
?Nombres complexes -module/argument
Énoncé
Soit \(z_1\) et \(z_2\) deux nombres complexes. Alors, \(|z_1+z_2|^2 + |z_1-z_2|^2\) est égal à :
Correction
Explication Générale
Utiliser : \(|z|^2= z\overline{z}\).
Pour aller plus loin :
?Nombres complexes -module/argument
Énoncé
Par définition, si \(x,y \in \mathbf{R}, \, e^{x+iy} = e^x \cdot e^{iy}= e^x (\cos y +i \sin y)\). Soit \(z=e^{e^{i\theta}}\), où \(\theta\) est un réel. Quelles sont les assertions vraies ?
Correction
Explication Générale
\(z= e^{\cos \theta + i \sin \theta}= e^{\cos\theta}\cdot e^{i \sin \theta}. \) Donc \(|z|=e^{\cos \theta} \) et \(\arg z = \sin \theta \, [2\pi]\).
Pour aller plus loin :
?Nombres complexes -module/argument
Énoncé
Soit \(z=e^{i\theta} + e^{i\phi} ,\theta, \phi \in \mathbf{R}\) tels que \(-\pi < \theta - \phi < \pi\). Quelles sont les assertions vraies ?
Correction
Explication Générale
\( z=e^{i\frac{\theta+\phi}{2}} (e^{i\frac{\theta-\phi}{2}} + e^{i\frac{\phi - \theta}{2}}) = 2 \cos (\frac{\theta-\phi}{2}) e^{i\frac{\theta+\phi}{2}}\). Comme \(\theta-\phi \in ]-\pi,\pi[\), \(\cos (\frac{\theta-\phi}{2}) > 0\). On déduit que : \(|z|=2\cos (\frac{\theta-\phi}{2})\) et \(\arg z = \frac{\theta+\phi}{2} \, [2\pi]\).
Pour aller plus loin :
video : Argument et trigonométrie
?Nombres complexes -équations
Énoncé
Les racines carrées de \(i\) sont :
Correction
Explication Générale
On résout dans \(\mathbf{C}\) l'équation : \(z^2=i=e^{i\frac{\pi}{2}}\).
Pour aller plus loin :
?Nombres complexes -équations
Énoncé
On considère l'équation : \((E) : \, z^2+z+1=0\), \(z\in \mathbf{C}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Les solutions complexes d'une équation du second degré \(az^2+bz+c=0\) sont \(z_1=\frac{-b+\delta}{2a}\) et \(z_1=\frac{-b-\delta}{2a}\), où \(\delta\) est une racine carrée de \(\Delta=b^2-4ac\).
Pour aller plus loin :
?Nombres complexes - équation
Énoncé
On considère l'équation : \((E) : \, z^2-2iz-1-i=0\), \(z\in \mathbf{C}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Utiliser la méthode de résolution d'une équation du second degré.
Pour aller plus loin :
exercices : Nombres complexes
?Nombres complexes - racine cubique
Énoncé
Les racines cubiques de \(-8\) sont :
Correction
Explication Générale
On résout l'équation \(z^3=-8 = 2^3e^{i\pi}\), en utilisant l'écriture géométrique.
Pour aller plus loin :
video : Argument et trigonométrie
exercices : Nombres complexes
?Nombres complexes -module/argument
Énoncé
Soit \(z\in \mathbf{C}\) tel que \(|z-1|=|z+1|\) . Quelles sont les assertions vraies ?
Correction
Explication Générale
Soit \(z\) tel que \(|z-1|=|z+1|\), \(M\) le point du plan d'affixe \(z\), \(A\) et \(B\) les points d'affixe \(-1\) et \(1\) respectivement. Alors, \(M\) est équidistant de \(A\) et \(B\).
Pour aller plus loin :
video : Nombres complexes et géométrie
exercices : Nombres complexes
?Nombres complexes - équations complexes
Énoncé
On considère l'équation \((E) : \, z^8= \overline{z}, \, z\in \mathbf{C}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Remarquer que si \(z\) est une solution de \((E)\), \(|z|^8=|\overline{z}|=|z|\), donc si \(z\) n'est pas nul, \(|z|=1\). Par conséquent, \(z\) est une solution non nulle de \((E)\) si et seulement si \(z^9=z\overline{z}=1\).
Pour aller plus loin :
video : Argument et trigonométrie
exercices : Nombres complexes
?Suites réelles - calcul de limite
Énoncé
Soit \(\displaystyle u_n=\frac{n^2+1}{2n^2-1}\) et \(\displaystyle v_n=\frac{2n+1}{n^2-1}\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
D'abord, \(\displaystyle u_n=\frac{n^2\left(1+\frac{1}{n^2}\right)}{n^2\left(2-\frac{1}{n^2}\right)}=\frac{1+\frac{1}{n^2}}{2-\frac{1}{n^2}}\). Or, \(\displaystyle \lim _{n\to +\infty}\frac{1}{n^2}=0\). Donc \(\displaystyle \lim _{n\to +\infty}u_n=\frac{1+0}{2-0}=\frac{1}{2}\). De même, \(\displaystyle v_n=\frac{n\left(2+\frac{1}{n}\right)}{n^2\left(1-\frac{1}{n^2}\right)}=\frac{1}{n}\times\frac{2+\frac{1}{n}}{1-\frac{1}{n^2}}\) et donc \(\displaystyle \lim _{n\to +\infty}v_n=0\).
Pour aller plus loin :
video : Limite
?Suites réelles - calcul de limite
Énoncé
Soit \(n\) un entier strictement supérieur à \(1\) et soit \(\displaystyle u_n=\sqrt{n+1}-\sqrt{n}\) et \(\displaystyle v_n=\cos\left(\frac{n^2+1}{n^2-1}\pi\right)\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
D'abord, \(\displaystyle u_n=\frac{\left(\sqrt{n+1}-\sqrt{n}\right)\left(\sqrt{n+1}+\sqrt{n}\right)}{\sqrt{n+1}+\sqrt{n}}=\frac{1}{\sqrt{n+1}+\sqrt{n}}\) et donc \(\displaystyle \lim _{n\to +\infty}u_n=0\) car \(\displaystyle \lim _{n\to +\infty}\left(\sqrt{n+1}+\sqrt{n}\right)=+\infty\). Par ailleurs, \(\displaystyle \frac{n^2+1}{n^2-1}\pi=\frac{n^2\left(1+\frac{1}{n^2}\right)}{n^2\left(1-\frac{1}{n^2}\right)}\pi=\frac{1+\frac{1}{n^2}}{1-\frac{1}{n^2}}\pi.\) Donc \(\displaystyle \lim _{n\to +\infty}\frac{n^2+1}{n^2-1}\pi=\pi\), et par suite, \(\displaystyle \lim _{n\to +\infty}v_n=\cos (\pi)=-1\).
Pour aller plus loin :
video : Limite
?Suites réelles - étude d'une suite
Énoncé
Soit \(n\) un entier naturel et soit \(\displaystyle u_n=\ln \left(1+n\mathrm{e}^{-n}\right)\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
Par croissances comparées, \(\displaystyle \lim _{n\to +\infty}n\mathrm{e}^{-n}=0\) et, par continuité de la fonction logarithme \(\lim _{n\to +\infty}u_n=\ln \left[\lim _{n\to +\infty}\left(1+n\mathrm{e}^{-n}\right)\right]=\ln (1)=0.\) Donc, \((u_n)\) converge et sa limite est \(0\). En outre, elle est bornée comme toute suite convergente.
Pour aller plus loin :
video : Limite
?Suites réelles - étude de convergence
Énoncé
Soit \(n\in\mathbb N^*.\) Soit \(\displaystyle u_n=\sin\left(\frac{2n\pi}{3}\right)\) et \(\displaystyle v_n=\sin\left(\frac{3}{2n\pi}\right)\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On a : \(\displaystyle \lim _{n\to +\infty}\frac{3}{2n\pi}=0\mbox{ donc }\displaystyle \lim _{n\to +\infty}\sin\left(\frac{2n\pi}{3}\right)=\sin\left(\lim _{n\to +\infty}\frac{3}{2n\pi}\right)=\sin 0=0\) par continuité de la fonction sinus. Ainsi, \((v_n)\) converge et sa limite est \(0\). Par ailleurs, \(u_{3n}=\sin (2n\pi)=0\mbox{ et }u_{3n+1}=\sin \left(\frac{2\pi}{3}\right)=\frac{\sqrt{3}}{2}.\) On trouve, d'après le théorème des suites extraites, \((u_n)\) diverge ; elle n'a pas de limite.
Pour aller plus loin :
video : Théorèmes de convergence
?Suites réelles - étude de deux suites
Énoncé
Soit \(n\) un entier naturel non nul et soit \(\displaystyle u_n=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\dots+\frac{1}{n^2}\) et \(\displaystyle v_n=u_n+\frac{1}{n}\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On vérifie que \((u_n)\) est croissante, \((v_n)\) est décroissante et que \(\displaystyle \lim _{n\to +\infty}(u_n-v_n)=0.\) Donc \((u_n)\) et \((v_n)\) sont adjacentes. En conséquence, elles convergent vers la même limite finie.
Pour aller plus loin :
video : Théorèmes de convergence
?Suites réelles - étude d'une suite
Énoncé
Soit \((u_n)\) une suite réelle. On suppose que \(\displaystyle u_n\geq \sqrt{n}\) pour tout \(n\geq 0\). Que peut-on en déduire ?
Correction
Explication Générale
Si \((u_n)\) était majorée, il en serait de même pour \(\sqrt{n}\) ce qui est absurde. Donc \((u_n)\) est une suite non majorée. Par passage à la limite, on a : \(\lim _{n\to +\infty}u_n\geq \lim _{n\to +\infty}\sqrt{n}=+\infty\Rightarrow \displaystyle \lim _{n\to +\infty}u_n=+\infty.\)
Pour aller plus loin :
video : Premières définitions
video : Limite
?Suites réelles - étude d'une suite
Énoncé
Soit n un entier plus grand que 1 et soit \(\displaystyle u_n=\sum _{k=1}^n\frac{1}{k(k+1)}\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
Le terme \(u_n\) est une somme télescopique. En effet, on vérifie que, pour tout \(k\geq 1\), \(\frac{1}{k(k+1)}=\frac{1}{k}-\frac{1}{k+1}\Rightarrow u_n=1-\frac{1}{n+1}.\) Donc \((u_n)\) est convergente et sa même limite est \(1\).
Pour aller plus loin :
video : Premières définitions
video : Limite
?Intégrales et primitives
Énoncé
La fonction \(x\mapsto \int_1^x \ln (t)dt\) vaut :
Correction
Explication Générale
On a par intégration par parties :
\(\int_1^x \ln (t)dt=\int_1^x \ln (t) \cdot 1dt=[t \ln(t)]^x_1 -\int_1^x t \frac{1}{t}dt=x\ln(x)- \ln(1) - \int_1^x 1dt=x\ln (x)-(x-1)=x\ln (x)-x+1\).
?Intégrales et primitives
Énoncé
La fonction \(x\mapsto \int_0^x te^{t} dt\) vaut :
Correction
Explication Générale
Par intégration par parties on a :
\(\int_0^x te^{t} dt= [t e^t]^x_0 -\int_0^x e^t\cdot 1 dt=xe^x-[e^t]_0^x=xe^x-e^x+1\).
?Intégrales et primitives
Énoncé
Quelle est la valeur de \(\int_{0}^{1}x\exp(x) \,dx\) ?
Correction
Explication Générale
Posons \(u(x)=x\) et \(v'(x)=\exp(x)\). Alors \(u'(x)=1\) et \(v(x)=\exp(x)\).
En intégrant par parties, on a donc :
\(\begin{eqnarray*}\int_{0}^{1}x\exp(x), dx&=& \int_{0}^{1}u(x)v'(x) \,dx\\&=& [u(x)v(x)]_0^1-\int_{0}^{1}u'(x)v(x) \,dx\\&=& [x\exp(x)]_0^1-\int_{0}^{1}\exp(x) \,dx\\&=& [x\exp(x)]_0^1-[\exp(x)]_0^1\\&=& \exp(1)-\exp(1)+\exp(0)\\&=& \exp(0)\\&=& 1\end{eqnarray*}\) et \(\int_{0}^{1}x\exp(x) \,dx=1\)
?Intégrales et primitives
Énoncé
Déterminer \(\int x\cos(x)\,dx\).
Correction
Explication Générale
Posons \(u(x)=x\) et \(v'(x)=\cos(x)\). Alors \(u'(x)=1\) et \(v(x)=\sin(x)\).
Ainsi par intégration par parties, on a :
\(\begin{eqnarray*}\int x\cos(x)\,dx&=&\int u(x)v'(x)\,dx\\&=& [u(x)v(x)]-\int u'(x)v(x)\,dx\\&=& [x\sin(x)]-\int\sin(x)\,dx\\&=& [x\sin(x)]+[\cos(x)]\\&=& x\sin(x)+\cos(x)+C\end{eqnarray*}\)
?Intégrales et primitives
Énoncé
Déterminer \(\int x\cos(\pi x)\,dx\).
Correction
Explication Générale
Posons \(u(x)=x\) et \(v'(x)=\cos(\pi x)\), alors \(u'(x)=1\) et \(v(x)=\frac{\sin(\pi x)}{\pi}\).
Ainsi, en intégrant par parties :
\(\begin{eqnarray*}\int x\cos(\pi x)\,dx&=&\int u(x)v'(x)\,dx \\&=& [u(x)v(x)]-\int u'(x)v(x)\,dx\\&=& [\frac{x\sin(\pi x)}{\pi}]-\int \frac{\sin(\pi x)}{\pi}\,dx\\&=& [\frac{x\sin(\pi x)}{\pi}]-\frac{1}{\pi}\int \sin(\pi x)\,dx\\&=& [\frac{x\sin(\pi x)}{\pi}]+\frac{1}{\pi}\left[\frac{\cos(\pi x)}{\pi}\right]\\&=& \frac{x\sin(\pi x)}{\pi}+\frac{\cos(\pi x)}{\pi^2}+ C\end{eqnarray*}\)
?Intégrales et primitives
Énoncé
Déterminer \(\int x e^{-x} \,dx\).
Correction
Explication Générale
Posons \(u(x)=x\) et \(v'(x)=\exp(-x)\) alors \(u'(x)=1\) et \(v(x)=-\exp(-x)\).
Ainsi, en intégrant par parties :
\(\begin{eqnarray*}\int x e^{-x}\,dx&=& \int u(x)v'(x)\,dx\\&=&[u(x)v(x)]-\int u'(x)v(x)\,dx\\&=&[-x e^{-x}]+\int e^{-x}\,dx\\&=& [-xe^{-x}]+[-e^{-x}]\\&=& -xe^{-x}-e^{-x}+C\\&=& -e^{-x}(x+1)+C \end{eqnarray*}\)
?Intégrales et primitives
Énoncé
Identifier une primitive de la fonction \(f(x)=x \sin x\).
Correction
Explication Générale
On réalise une intégration par parties avec \(u(x)=x\), \(v(x)=-\cos x\), ce qui donne \(u'(x)=1\) et \(v'(x)=\sin x\) et \(\int x \sin x \,dx = \left[ -x \cos x\right] - \int (-\cos x) \,dx= \left[ -x \cos x + \sin x\right]\).
?Intégrales et primitives
Énoncé
Identifier une primitive de la fonction \(f(x)=x e^{-x}\).
Correction
Explication Générale
On réalise une intégration par parties avec \(u(x)=x\), \(v(x)=-e^{-x}\), ce qui donne \(u'(x)=1\) et \(v'(x)=e^{-x}\) et \(\int x e^{-x} \,dx = \left[ -x e^{-x}\right] - \int (-e^{-x}) \,dx= \left[ -x e^{-x} -e^{-x}\right]\).
?Dérivation réciproque
Énoncé
Coche la ou les bonne(s) réponse(s)
Correction
Explication Générale
Revoir les propriétés sur la dérivée et la bijection réciproque
?Dérivation réciproque
Énoncé
La fonction \(f\) définie par \(f(x) =\frac{1}{\cos x}\) sur l'intervalle \(]0 ;\frac{\pi}{2}[.\) est une bijection dérivable de \(]0 ;\frac{\pi}{2}[\) vers \(]1;+\infty[\), alors sa bijection réciproque \(f^{-1}\) admet comme fonction dérivée :
Correction
Explication Générale
On utilise la dérivée d'une fonction réciproque
?Dérivation réciproque
Énoncé
Soit la fonction \(f\) définie par \(f(x) = xe^x\) sur l'intervalle \([0; +∞\)[ et \(f(1) = e\). Elle admet une bijection réciproque\( f^{-1}\) définie sur \([0; +∞[.\)
On a :
Correction
Explication Générale
On utilise la propriété relative à la dérivée d'une fonction réciproque
?Dérivation réciproque
Énoncé
Soit la fonction \(f\) définie par \(f(x)=-1+ e^{x-1}+ lnx\) sur l'intervalle \(]0; +∞[\) et \(f(1) = 0\) Elle admet une bijection réciproque \(f^{-1}\) définie sur \(R\).
La tangente au point d'abscisse\( 0\) à la courbe de \(f^{-1}\) a pour équation :
Correction
Explication Générale
On utilise la propriété relative à la dérivée d'une fonction réciproque en un point donné
?Dérivation-reciproque
Énoncé
Soit la fonction \(f\) définie par \(f(x)=4x+ sin^4 (x)\) sur \(R\) et \(f(0) = 0\) Elle admet une bijection réciproque f^{-1} définie sur\( R\).
La tangente au point d'abscisse\( 0\) à la courbe de \(f^{-1}\) a pour équation :
Correction
Explication Générale
On utilise la propriété relative à la dérivée d'une fonction réciproque en en un point donné
?Dérivée-Fonctions trigonométriques
Énoncé
Soit la fonction \(f\) définie sur \(R\) par \(f(x) = sin(3x) – sin^3 (x).\) \(f\) est dérivable sur \(\mathbb{R}.\)
Trois propositions sont faites dont une seule est juste, coche la.
Correction
Explication Générale
On utilise la dérivée des fonctions cosinus, sinus
?Dérivée-Fonctions trigonométriques
Énoncé
Soit la fonction \(f\) définie sur\( R\) par \(f(x) = cos2x – cosx – 2\). \(f\) est dérivable sur \(\mathbb{R}\).
Trois propositions sont faites dont une seule est juste, coche la.
Correction
?Dérivée-Foctions trigonométriques
Énoncé
Soit la fonction \(f\) définie sur \(R\) par \(f(x) = cos^2 (x)sin(x)\). \(f\) est dérivable sur \(\mathbb{R}\).
Trois propositions sont faites dont une seule est juste, coche la.
Correction
?Dérivée-Fonctions trigonométriques
Énoncé
Soit la fonction \(f\) définie sur\(\mathbb{R}\) par \(f(x) = sin(2x^2 -1).\) \( f\) est dérivable sur \(\mathbb{R}\)
Trois propositions sont faites dont une seule est juste, coche la.
Correction
?Dérivée-Fonctions trigonométriques
Énoncé
Soit la fonction \(f\) définie sur ]\( -\frac{\pi}{2} ;+ \frac{\pi}{2}\)[ par\( f(x)= tanx+2sinx.\) \(f\) est dérivable sur ] \(-\frac{\pi}{2} ;+ \frac{\pi}{2}\)[
Trois propositions sont faites dont une seule est juste, coche la
Correction
?Dérivée-Fonction puissance
Énoncé
Soit la fonction \(f(x)=x^{\frac{3}{2}}(1-x)^{\frac{1}{2}}\)
Cocher les affirmations vraies.
Correction
?Dérivée d'une fonction puissance
Énoncé
Soit la fonction définie sur [0;8] par : \( f(x)=\left(4-x^{2/3}\right)^{3/2}\)
Cocher les affirmations vraies.
Correction
Explication Générale
On utilise la propriété relative à la dérivée d'une fonction puissance
?Dérivée-Fonction puissance
Énoncé
Soit la fonction \(g\) définie par\( g(x)=x^{\frac{-5}{6}}\) .
Cocher les affirmations vraies.
Correction
?Dérivée-Fonction puissance
Énoncé
Soit la fonction\( h\) définie par \(h(x) = (ln2)^x\)
Cocher les affirmations vraies.
Correction
?Fonctions numériques - Logarithme et Exponentielle
Énoncé
Cochez les bonnes réponses
Correction
Explication Générale
Bien réviser votre cours sur les propriétés algébriques de la fonction logarithme.
?Transformation
Énoncé
Coche la ou les bonne(s) réponse(s)
Correction
?Transformation
Énoncé
Coche la ou les bonne(s) réponse(s)
Correction
?Transformation
Énoncé
Coche la ou les bonne(s) réponse(s)
Correction
?Transformation
Énoncé
Coche la ou les conne(s) réponse(s)
Correction
?Fonction logarithme népérien
Énoncé
Coche la bonne réponse.
L'équation \(\ln (3+x)=\ln 3+\ln x\) a pour ensemble solution
Correction
?Fonction logarithme népérien
Énoncé
Coche la bonne réponse.
L'équation \(\ln(3x)=3\ln x\) a pour ensemble solution :
Correction
?Fonction logarithme népérien
Énoncé
Coche la bonne réponse.
L'inéquation \(\ln(\frac{1}{x}) \leq 0\) a pour ensemble solution :
Correction
?Fonction logarithme népérien
Énoncé
Coche la bonne réponse.
L'inéquation \(2+\ln (x)<0\) a pour ensemble solution :
Correction
?Fonction logarithme népérien
Énoncé
Coche la bonne réponse.
L'équation \(\ln^2(x)-\ln (x)-6=0\) a pour ensemble solution :
Correction
?Fonction logarithme népérien
Énoncé
Coche la bonne réponse.
La limite quand \(x\) tend vers \(3^{-}\) de la fonction \(f\) définie par :\( f(x) =\ln (9-x^2)\) est :
Correction
?Fonction logarithme népérien
Énoncé
Cocher la bonne réponse.
La limite quand \(x\) tend vers \(e\) de la fonction \(f\) définie par : \(f(x)=\ln(1-\ln x)\) est :
Correction
?Fonction logarithme népérien
Énoncé
Cocher la bonne réponse.
La limite quand \(x\) tend vers \(+\infty\) de la fonction \(f\) définie par :
\(f(x)= x-\ln x\) est :
Correction
?Fonction logarithme népérien
Énoncé
Cocher la bonne réponse.
La limite quand \(x\) tend vers \(+\infty\) de la fonction\( f\) définie par :
\(f(x)=\frac{x}{\ln x}\) est :
Correction
?Fonction logarithme népérien
Énoncé
Cocher la bonne réponse.
La limite quand \(x\) tend vers \(e\) de la fonction \(f\) définie par :
\(f(x)=\frac{\ln x - 1}{x-e}\) est :
Correction
?Fonction logarithme népérien
Énoncé
Cocher la bonne réponse.
Soit la fonction \(f\) définie par :\(f(x)=\frac{1}{2x+4}\). Une primitive de \(f\) sur \(]-\infty ;2[\) est la fonction \(g\) définie par :
Correction
?Sens de variation
Énoncé
Soit la fonction f définie sur \([0.+\infty[\) par : \(f(x)=\sqrt{x^2+x}\)
Correction
?Sens de variation
Énoncé
Soit la fonction \(f\) définie sur \([0 ;\pi]\) par : \(f(x)=\cos^2(x)-\cos (x)-2\)
Correction
?Sens de variation
Énoncé
Soit la fonction \(f\) définie sur \([0 ;\frac{\pi}{2}]\) par \(f(x)=\cos^2(x)\sin(x)\)
Correction
?Sens de variation
Énoncé
Soit la fonction \(f\) définie sur \([0 ;+\infty[\) par \(f(0)=0\) et \(f(x)=x\ln(x)\) si \(x>0\)
Correction
?Sens de variation
Énoncé
Soit \(f\) la fonction définie sur \(]0 ;+\infty[\) par \(f(x)=\frac{x}{\ln x}\)
Correction
?Sens de variation
Énoncé
Soit la fonction \(f\) définie sur \(]-\infty ;+\infty[\) par \(e^{2x}-2e^x\)
Correction
?Sens de variation
Énoncé
Soit la fonction \(f\) définie sur \(]0 ;+\infty[\) par \(\ln (e^x-1)\)
Correction
?Sens de variation
Énoncé
Soit \(f\) la fonction définie sur \(]-\infty ;+\infty[\) par \(f(x)=\frac{1}{e^x+1}\)
Correction
?Sens de variation
Énoncé
Coche la ou les bonne(s) réponse(s)
Soient \(f\) et \(g\) deux fonctions définies sur \(\mathbb{R}\) vérifiant :
Pout tout \(x \in \mathbb{R}\), \(f(x)=e^{2g(x)}\). On a :
Correction
?Sens de variation
Énoncé
Soit la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x)=1+exe^x\)
Correction
?Sens de variation
Énoncé
Soit la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x)=(\ln2)^x\)
Correction
?Sens de variation
Énoncé
Soit la fonction \(f\) définie sur \(\mathbb{R}\) par \((\cos 1)^x\)
Correction
?Sens de variation
Énoncé
Soit la fonction \(f\) définie sur\(\mathbb{R}^*_+\) par \(f(x)=x^{0,6}\)
Correction
?Diviseurs et multiples - Décomposition en produit de facteurs
Énoncé
Cochez la ou les bonnes réponses
Correction
Explication Générale
\(b=aq\) et \(c=aq'\) alors \(bc=a^2qq'\)
\(2 \vert 2\) et \(2\vert 4\) alors que \(4\) ne divise pas \(6\).
Voir algorithme d'Euclide
?Diviseurs et multiples - Système de numération
Énoncé
Cochez la ou les bonnes réponses
Correction
Explication Générale
Il suffit juste de faire le calcul, on pourra utiliser l'écriture en base \(b\) d'un nombre.
?Diviseurs et multiples - Système de numération
Énoncé
Cochez la ou les bonnes réponses
Correction
Explication Générale
Il suffit juste de faire le calcul, on pourra utiliser l'écriture en base \(b\) d'un nombre.
?Diviseurs et multiples - Système de numération
Énoncé
Cochez la ou les bonnes réponses
Correction
Explication Générale
Il suffit juste de faire le calcul, on pourra utiliser l'écriture en base \(b\) d'un nombre.
?Diviseurs et multiples - Equations diophantiennes linéaires
Énoncé
L'équation diophantienne linéaire suivante \(12x+16y=6\) admet :
Correction
Explication Générale
Pour l'équation \(ax+by=c\) n'admet pas de solution si \(a\wedge b\) ne divise pas \(c\).
?Diviseurs et multiples - Equations diophantiennes linéaires
Énoncé
L'équation diophantienne linéaire suivante \(5x+6y=7\) admet :
Correction
Explication Générale
l'équation \(ax+by=c\) admet une infinité de solutions si \(a\wedge b\) divise \(c\).
?Diviseurs et multiples - Equations diophantiennes linéaires
Énoncé
L'équation diophantienne linéaire suivante \(3x+6y=5\) admet :
Correction
Explication Générale
l'équation \(ax+by=c\) n'admet pas de solutions si \(a\wedge b\) ne divise pas \(c\).
?Equations dans Z
Énoncé
On considère l'équation : \( x^2- x+4 \equiv 0 \pmod{6}\)
Correction
?Divisibilité - petit théorème de Fermat
Énoncé
Quelle est la valeur de \(3^{2020}\pmod{17}\)?
Correction
Explication Générale
Utiliser le petit théorème de Fermat (17 est premier). On réduit la puissance en la divisant par \(16\) : \(3^4\equiv 13={17}\).
?Divisibilité - petit théorème de Fermat
Énoncé
Quelle est la valeur de \(5^{55555}\pmod{7}\)?
Correction
Explication Générale
Utiliser le petit théorème de Fermat (7 est premier). On réduit la puissance en le divisant par \(6\).
?Divisibilité - congruences
Énoncé
Cochez les bonnes réponses
Correction
Explication Générale
\(a\equiv b\pmod c\) signifie que \(c|(a-b)\)
?Divisibilité - Congruences
Énoncé
Cochez les bonnes réponses
Correction
Explication Générale
\(a\equiv b\pmod c\) signifie que \(c|(a-b)\)
?Divisibilité - congruences
Énoncé
Cochez les bonnes réponses
Correction
Explication Générale
\(a\equiv b\pmod c\) signifie que \(c|(a-b)\)
?Divisibilité - petit théorème de Fermat
Énoncé
Quelle est la valeur de \(2010^{2019}\pmod{17}\)?
Correction
Explication Générale
Utiliser le petit théorème de Fermat (17 est premier). On réduit la puissance en la divisant par \(16\)
?Divisibilité - petit théorème de Fermat
Énoncé
Quelle est la valeur de \(2020^{2021}\pmod{17}\)?
Correction
Explication Générale
Utiliser le petit théorème de Fermat (17 est premier). On réduit la puissance en la divisant par \(16\)
?Divisibilité - petit théorème de Fermat
Énoncé
Cochez les affirmations qui sont correctes. \(n=77+77+77+77+77+77+77+77+77+77+77+77+77+77+77+77\)
Correction
?Divisibilité - petit théorème de Fermat
Énoncé
Cochez les affirmations qui sont correctes.
Correction
?Divisibilité - petit théorème de Fermat
Énoncé
Cochez les affirmations qui sont correctes.
Correction
?Divisibilité - pgcd et ppcm
Énoncé
Cochez la ou les bonnes réponses :
Correction
Explication Générale
Il suffit de décomposer les nombres
?Divisibilité - pgcd et ppcm
Énoncé
Cochez la ou les bonnes réponses :
Correction
Explication Générale
Il suffit de décomposer les nombres
?Divisibilité - pgcd et ppcm
Énoncé
Cochez la ou les bonnes réponses :
Correction
Explication Générale
Il suffit de décomposer les nombres
pgcd(x,y)=pgcd(y,x)
?Divisibilité - pgcd et ppcm
Énoncé
Cochez la ou les bonnes réponses :
Correction
Explication Générale
Il suffit de décomposer les nombres
pgcd(x,y)=pgcd(y,x)
?Divisibilité - pgcd et ppcm
Énoncé
Cochez la ou les bonnes réponses :
Correction
Explication Générale
Il suffit de décomposer les nombres
?Divisibilité - pgcd et ppcm
Énoncé
\(x\) et \(y\) étant des entiers relatifs, cochez la ou les bonnes réponses :
Correction
Explication Générale
Il suffit de décomposer les nombres et de prendre la valeur absolue par définition même du ppcm et du pgcd
?Divisibilité - pgcd et ppcm
Énoncé
Pour \(a,b,c\) des entiers, cochez la ou les bonnes réponses :
Correction
Explication Générale
Il suffit d'utiliser la définition du ppcm. C'est le plus petit des multiples communs ordonnés par la divisibilité.
?Divisibilité - pgcd et ppcm
Énoncé
Pour \(a,b,c\) des entiers, cochez la ou les bonnes réponses :
Correction
Explication Générale
Il suffit d'utiliser les propriétés du ppcm
?Divisibilité - pgcd et ppcm
Énoncé
Pour \(a,b,c\) des entiers, cochez la ou les bonnes réponses :
Correction
Explication Générale
Il suffit d'utiliser les propriétés du pgcd
?Divisibilité - critères de divisibilité
Énoncé
Cochez la ou les bonnes réponses :
Correction
Explication Générale
Revoir les critères de divisibilité par \(3,6,9\)
?Divisibilité - critères de divisibilité
Énoncé
Cochez la ou les bonnes réponses :
Correction
Explication Générale
Revoir les critères de divisibilité par \(3,5,10,2\)
?Divisibilité - critères de divisibilité
Énoncé
Cochez la ou les bonnes réponses :
Correction
Explication Générale
Revoir les critères de divisibilité.
?Intégrale d eproduit de fonctions
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(B=\int_0^{\frac{\pi}{2}}x^2sin(3x)~dx\)
Correction
?Intégrale de produit de fonctions
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(A=\int_1^x2t^3e^{t^2+1}~dt\), \(x\) étant un réel.
Correction
?Intégrale de produit de fonctions
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(C=\int_1^ex(ln x)^2~dx\)
Correction
?Intégrales et aires
Énoncé
\((D)\) est l'ensemble des points \(M(x , y)\) du plan tels que : \(\left \{\begin{array}{rcl} 0 \leq x \leq \pi \\ 0 \leq y \leq \sin x \end{array}\right.\). L'unité graphique est 2 cm. L'aire de \((D)\) en \(cm^2\) est :
Correction
?Intégrales et aires
Énoncé
\((D)\) est l'ensemble des points \(M(x , y)\) du plan tels que : \(\left \{\begin{array}{rcl} 0 \leq x \leq \pi \\ 0 \leq y \leq \sin x \end{array}\right.\). L'unité graphique est \(\frac{6}{\pi}\) cm sur l'axe des abscisses et 4 cm sur l'axe des ordonnées. L'aire de \((D)\) en \(cm^2\) est :
Correction
?Intégrales et aires
Énoncé
\((D)\) est l'ensemble des points \(M(x , y)\) du plan tels que : \(\left \{\begin{array}{rcl} -1 \leq x \leq 0 \\ 0 \leq y \leq x^2-4x \end{array}\right.\). L'aire de \((D)\) en unités d'aire est :
Correction
?Intégrales et aires
Énoncé
\((D)\) est l'ensemble des points \(M(x , y)\) du plan tels que : \(\left \{\begin{array}{rcl} 0 \leq x \leq 4 \\ x^2-4x \leq y \leq 0 \end{array}\right.\). L'aire de \((D)\) en unités d'aire est :
Correction
?Intégrales et aires
Énoncé
Considérons la fonction \(f\) définie sur \([-\pi ;\pi]\) par \(f(x)=x-sinx\) et \((C_f)\) sa courbe représentative dans un repère orthonormal du plan. L'aire en unités d'aire, comprise entre \((C_f)\), l'axe des abscisses et les droites d'équations \(x=0\) et \(x=\pi\) est :
Correction
?Intégrales de fonctions puissances
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(A=\int_0^{\frac{\pi}{2}}\cos^4(x)~dx\)
Correction
?Intégrales de fonctions puissances
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(A=\int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\sin^6(x)~dx\)
Correction
?Intégrales de fonctions puissances
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(A=\int_0^{\frac{\pi}{3}}\sin^2(x)~dx\)
Correction
?Intégrales de fonctions puissances
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(A=\int_1^2\frac{1}{x^6}~dx\)
Correction
?Intégrales et moyenne
Énoncé
Soit la fonction \(f\) définie sur \([-1 ; 3]\) par :\( f(x) = x^3\). La valeur moyenne de \(f\) sur \([ -1 ; 3]\) est :
Correction
?Intégrales et moyenne
Énoncé
Soit la fonction\( f\) définie sur \([0 ; \pi]\) par : \(f(x) = cos^2 (x)\). La valeur moyenne de f sur \([0 ; \pi]\) est :
Correction
?Intégrales et moyenne
Énoncé
Soit la fonction\( f\) définie sur \([1 ; 4]\) par : \(f(x) = \frac{1}{x}\). La valeur moyenne de f sur \([1 ; 4]\) est :
Correction
?Intégrales et moyenne
Énoncé
Soit la fonction \(f\) définie sur \([0 ; \frac{\pi}{2}]\) par : \(f(x) = cos^5(x).\) La valeur moyenne de \(f\) sur \( [0 ; \frac{\pi}{2}]\) est :
Correction
?Intégrales et moyenne
Énoncé
Soit la fonction\( f\) définie sur \([0 ; \frac{\pi}{6}]\) par : \(f(x) = sin^3 (2x)\). La valeur moyenne de \(f\) sur \([0 ; \frac{\pi}{6}]\) est :
Correction
?Intégrales simples
Énoncé
Soit l'intégrale \(I=\int_0^{\frac{\pi}{2}}sin^2(x)cos(x) ~dx\). Coche la bonne réponse.
Correction
?Intégrales simples
Énoncé
Pour l'intégrale suivante, coche la bonne réponse. \(J=\int_1^e\frac{ln x}{x} ~dx\)
Correction
?Intégrales simples
Énoncé
Pour l'intégrale suivante, coche la bonne réponse. \(K=\int_1^2\frac{1}{x^2}e^{\frac{1}{x}}~ dx\)
Correction
?Intégrales simples
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(L=\int_1^0\frac{4x^3+8x}{(x^4+4x^2+2)^3}~dx\)
Correction
?Intégrales simples
Énoncé
Pour l'intégrale suivante, coche la bonne réponse \(M=\int_0^2(1-\vert t-1\vert)^3 ~dx\)
Correction
?Intégrales simples
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(K=\int_{-107}^{107}(t^3+4sin^7(t))~dt\)
Correction
?Intégrales simples
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(O=\sum_{k=1}^{k=5}\int_k^{k+1}\sqrt{t}~dt\)
Correction
?Intégrales simples
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse.\(A=\int_0^1\frac{x^2}{\sqrt{1+2x^3}}~dx\)
Correction
?Intégrales simples
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(B=\int_{ln2}^{ln3}\frac{e^{2x}}{e^{2x}-1}~dx\)
Correction
?Intégrales simples
Énoncé
Pour l'intégrale suivante, cocher la bonne réponse. \(D=\int_1^x2te^{t^2+1}~dt\) \(x\) étant un réel.
Correction
?Intégrales et volumes
Énoncé
On considère la fonction numérique \(f\) définie par : \(f(x)=e^x\). Soit \((C_f)\) la courbe représentative de \(f\) dans un repère orthonormal \((O,\overrightarrow{i},\overrightarrow{j})\). \((O,\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})\) orthonormal de l'espace. Par rotation autour de l'axe \((O,\overrightarrow{i})\), le domaine plan limité par \((C_f)\), la droite \((O,\overrightarrow{i})\) et les droites d'équations \(x=-1\) et \(x=1\) engendrent un solide de révolution, noté\( (S)\). Le volume de \((S)\), unités de volume, est :
Correction
?Intégrales et volumes
Énoncé
On considère la fonction numérique \(f\) définie par : \(f(x)=sin^2 (x)\). Soit \((C_f)\) la courbe représentative de \(f\) dans un repère orthonormal \((O,\overrightarrow{i},\overrightarrow{j})\). \((O,\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})\) orthonormal de l'espace. Unité graphique 3 \(cm\)
Par rotation autour de l'axe \((O,\overrightarrow{i})\), le domaine plan limité par \((C_f)\), la droite \((O,\overrightarrow{i})\) et les droites d'équations \(x=0\) et \(x=\pi\) engendrent un solide de révolution, noté\( (S)\). Le volume de \((S)\), en \(cm^3\) est :
Correction
?Intégrales et volumes
Énoncé
On considère la fonction numérique \(f\) définie par : \(f(x)=x+\frac{lnx}{x}\). Soit \((C_f)\) la courbe représentative de \(f\) dans un repère orthonormal \((O,\overrightarrow{i},\overrightarrow{j})\). \((O,\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})\) orthonormal de l'espace. Unité graphique 3 \(cm\)
Par rotation autour de l'axe \((O,\overrightarrow{i})\), le domaine plan limité par \((C_f)\), la droite \((O,\overrightarrow{i})\) et les droites d'équations \(x=1\) et \(x=e\) engendrent un solide de révolution, noté\( (S)\). Le volume de \((S)\), en \(cm^3\) est :
Correction
?Intégrales et volumes
Énoncé
On considère la fonction numérique \(f\) définie par : \(f(x)=x^2\). Soit \((C_f)\) la courbe représentative de \(f\) dans un repère orthonormal \((O,\overrightarrow{i},\overrightarrow{j})\). \((O,\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})\) orthonormal de l'espace. Par rotation autour de l'axe \((O,\overrightarrow{i})\), le domaine plan limité par \((C_f)\), la droite \((O,\overrightarrow{i})\) et les droites d'équations \(x=0\) et \(x=2\) engendre un solide de révolution, noté\( (S)\). Le volume de \((S)\), unités de volume, est :
Correction
?Intégrales et volumes
Énoncé
On considère la fonction numérique \(f\) définie par : \(f(x)=\sin x\). Soit \((C_f)\) la courbe représentative de \(f\) dans un repère orthonormal \((O,\overrightarrow{i},\overrightarrow{j})\). \((O,\overrightarrow{i},\overrightarrow{j},\overrightarrow{k})\) orthonormal de l'espace. Par rotation autour de l'axe \((O,\overrightarrow{i})\), le domaine plan limité par \((C_f)\), la droite \((O,\overrightarrow{i})\) et les droites d'équations \(x=0\) et \(x=\pi\) engendrent un solide de révolution, noté\( (S)\). Le volume de \((S)\), unités de volume, est :
Correction
?Intégrales et inégalités
Énoncé
Soit \(f\) une fonction continue sur intervalle \(I\) et \(a\) et\( b\) des réels de \(I\) tels que\( a \leq b\), on a :
Correction
?Intégrales et inégalités
Énoncé
Soient \(f\) et \(g\) des fonctions continues sur un intervalle \(I\) et \(a\) et \(b\) des réels de \(I\) tels que \(a \leq b,\) on a :
Correction
?Intégrales et inégalités
Énoncé
Soit \(f\) une fonction continue sur intervalle\( I\) et \(a\) et \(b\) des réels de\( I\) tels que \(a \leq b\), on a :
Correction
?Intégrales et inégalités
Énoncé
Pour tout\( x\) élément de\( ]0 ; +\infty[\)on a :
Correction
?Intégrales et inégalités
Énoncé
Soit \(F\) la fonction de \([0 ; +\infty[\) dans \(\mathbb{R}\) définie par \(F(x)=\int_0^x \sin^2(\sqrt{t}) ~dt\)
Correction
?Intégrales et inégalités
Énoncé
Soient \(f, g\) deux fonctions numériques et \(a,b\in\mathbb R \). Cochez les bonnes réponses
Correction
?Intégrales et inégalités
Énoncé
Soient \(f, g\) deux fonctions numériques et \(a,b\in\mathbb R \). Cochez les bonnes réponses
Correction
Explication Générale
inégalités de la moyenne - intégrales de fonctions positives.
?Intégration par parties
Énoncé
Soit \(\int_0^\pi xsinx~+dx\). Coche la bonne réponse.
Correction
?Intégration par parties
Énoncé
Soit \(\int_1^elnx~ dx\). Coche la bonne réponse.
Correction
?EQUATIONS DIFFERENTIELLES DU PREMIER ORDRE SANS SECOND MEMBRE
Énoncé
L'équation différentielle : \(y'=\frac{1}{4}y\) a pour solutions les fonctions \(f\) qui à \(x\) associent :
Correction
?EQUATIONS DIFFERENTIELLES DU PREMIER ORDRE SANS SECOND MEMBRE
Énoncé
L'équation différentielle : \(y'=-\frac{5}{2} y\) a pour solutions les fonctions\( f\) qui à\( x\) associent :
Correction
?EQUATIONS DIFFERENTIELLES DU PREMIER ORDRE SANS SECOND MEMBRE
Énoncé
L'équation différentielle :\( 2y'-11y=0\) a pour solutions les fonctions \(f\) qui à \(x\) associent :
Correction
?EQUATIONS DIFFERENTIELLES DU PREMIER ORDRE SANS SECOND MEMBRE
Énoncé
L'équation différentielle :\( 3y+7y'=0\) a pour solutions les fonctions \(f\) qui à \(x\) associent :
Correction
?EQUATIONS DIFFERENTIELLES DU PREMIER ORDRE SANS SECOND MEMBRE
Énoncé
L'équation différentielle : \(-\cos (\alpha)y+y'=0\) \(\alpha \in [0 ;2 \pi]\) , a pour solutions les fonctions \(f\) qui à \(x\) associent :
Correction
?EQUATIONS DIFFERENTIELLES DU SECOND ORDRE SANS SECOND MEMBRE
Énoncé
L'équation différentielle :\( y'' – y' – 6y = 0\) a pour solutions les fonctions \(f\) qui à \(x\) associent :
Correction
?EQUATIONS DIFFERENTIELLES DU SECOND ORDRE SANS SECOND MEMBRE
Énoncé
L'équation différentielle : \(y'' – 2y' + 5y = 0\) a pour solutions les fonctions \(f\) qui à \(x\) associent :
Correction
?EQUATIONS DIFFERENTIELLES DU SECOND ORDRE SANS SECOND MEMBRE
Énoncé
L'équation différentielle : \(y''+ 4y' +4y = 0\) a pour solutions les fonctions \(f\) qui à\( x\) associent :
Correction
?EQUATIONS DIFFERENTIELLES DU SECOND ORDRE SANS SECOND MEMBRE
Énoncé
L'équation différentielle : \(y'' + 4y' = 0\) a pour solutions les fonctions \(f\) qui à\( x\) associent :
Correction
?EQUATIONS DIFFERENTIELLES DU SECOND ORDRE SANS SECOND MEMBRE
Énoncé
L'équation différentielle \(: 2y'' + 3y + y = 0\) a pour solutions les fonctions \(f\) qui à \(x\) associent :
Correction
?EQUATIONS DIFFERENTIELLES DU SECOND ORDRE SANS SECOND MEMBRE
Énoncé
L'équation différentielle : \(y'' - 2 y' + 5y = 0\) telle \(f(0) = 1\) et \(f '(0) = 3\), a pour solution la fonctions \(f\) qui à \(x\) associent :
Correction
?Produit mixte
Énoncé
Soit \((O,\overrightarrow{i}; \overrightarrow{j} ;\overrightarrow{k})\) un repère orthonormé de l'espace. On considère les vecteurs :
\(\overrightarrow{u}(1, -1, 1)\) ; \(\overrightarrow{v}(2, 3,-1)\) et \(\overrightarrow{w}( 1,2,3)\)
Le produit mixte des trois vecteurs ,\(\overrightarrow{u}\) , \(,\overrightarrow{v}\) \(,\overrightarrow{w}\) est :
Correction
?Produit mixte
Énoncé
Soit \((O,\overrightarrow{i}; \overrightarrow{j} ;\overrightarrow{k})\) un repère orthonormé de l'espace. On considère les vecteurs :
\(\overrightarrow{u}(1, -1, 1)\) ; \(\overrightarrow{v}(2, 3,-1)\) et \(\overrightarrow{w}( 1,2,3)\)
Le produit mixte des trois vecteurs ,\(\overrightarrow{u}\) , \(,\overrightarrow{v}\) \(,\overrightarrow{w}\) est :
Correction
?Produit mixte
Énoncé
Soit \((O,\overrightarrow{i}; \overrightarrow{j} ;\overrightarrow{k})\) un repère orthonormé de l'espace. On considère les vecteurs :
\(\overrightarrow{u}(1, -1, 1)\) ; \(\overrightarrow{v}(2, 3,-1)\) et \(\overrightarrow{w}( 1,2,3)\)
Le produit mixte des trois vecteurs ,\(\overrightarrow{u}\) , \(,\overrightarrow{v}\) \(,\overrightarrow{w}\) est :
Correction
?Produit mixte
Énoncé
Trois vecteurs \(\overrightarrow{u}\), \(\overrightarrow{v}\) et \(\overrightarrow{w}\) de l'espace sont coplanaires si leur produit mixte est différent de \( 0\).
Correction
?Produit vectoriel
Énoncé
Soit\( (O,\overrightarrow{i}; \overrightarrow{j} ;\overrightarrow{k})\) un repère orthonormé de l'espace. On considère les vecteurs :
\(\overrightarrow{u}(1, -1, 1)\) ; \(\overrightarrow{v}(2,3,-1)\) et \(\overrightarrow{w} ( 1,2,3)\).
Les coordonnées du produit vectoriel de \(\overrightarrow{u}\) par \(\overrightarrow{v}\) sont :
Correction
?Produit vectoriel
Énoncé
Soit \((O,\overrightarrow{i}; \overrightarrow{j} ;\overrightarrow{k})\) un repère orthonormé de l'espace. On considère les vecteurs :
\(\overrightarrow{u}(1, -1, 1)\) ; \(\overrightarrow{v}(2,3,-1)\) et \(\overrightarrow{w}( 1,2,3)\).
Les coordonnées du produit vectoriel de \(\overrightarrow{u}\) par \( \overrightarrow{w}\) sont :
Correction
?Produit vectoriel
Énoncé
Coche la ou les réponse(s) vraies.
Pour tous vecteurs \(\overrightarrow{u}\) , \(\overrightarrow{v}\) et \(\overrightarrow{w}\) et pour tout réel \(k\) :
Correction
?Produit vectoriel
Énoncé
Soit \((O,\overrightarrow{i}; \overrightarrow{j} ;\overrightarrow{k})\) un repère orthonormé de l'espace. On considère les vecteurs :
\(\overrightarrow{u}(1, -1, 1)\) ; \(\overrightarrow{v}(2,3,-1)\) et \(\overrightarrow{w}( 1,2,3)\).
Les coordonnées du produit vectoriel de \(\overrightarrow{v}\) par \( \overrightarrow{w}\) sont :
Correction
?Calcul barycentrique
Énoncé
Soient \(A, B\) et \(C\) des points non alignes, l'ensemble des points \(M\) du plan tels que:
\(\|3 \overrightarrow{MA}+\overrightarrow{MB}\|+\|3 \overrightarrow{MC}+\overrightarrow{MB}\|\) est :
Correction
?Calcul barycentrique
Énoncé
\(ABCD\) est un rectangle tel que : \(AB = 2\) et \(BC = 1\).
L'ensemble des points \(M\) du plan tels que: \(MA^2+ MB^2+ MC^2+ MD^2=10\) est :
Correction
?Calcul barycentrique
Énoncé
Soient \(A\) et \(B\) deux points distincts du plan, l'ensemble des points\( M\) tels que :
\(\frac{MA}{MB}\)=\( 1\) est :
Correction
?Calcul barycentrique
Énoncé
Soient \(A\) et \(B\) deux points distincts du plan, l'ensemble des points \(M\) tels que :
\(\frac{MA}{MB}\)= \(k\) avec\( k≠1\) et \(k≠0\) est :
Correction
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit les vecteurs représentés ci-dessous.
Quel produit scalaire est égal à 2 ?
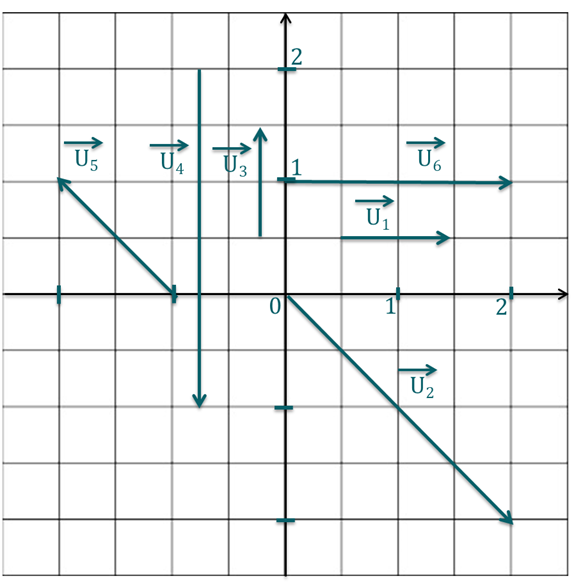
Correction
Explication Générale
On cherche un produit scalaire positif : il faut que les deux vecteurs impliqués soient dans le même sens.
Parmi les propositions, c'est donc uniquement possible pour : \( \overrightarrow{u_2}\cdot\overrightarrow{u_4} \); \(\overrightarrow{u_1}\cdot\overrightarrow{u_6}\) et \(\overrightarrow{u_3}\cdot\overrightarrow{u_5}\).
On calcule alors ces trois produits scalaires :
\(\overrightarrow{u_2}\cdot\overrightarrow{u_4}= \begin{pmatrix}2\\-2\end{pmatrix} \cdot \begin{pmatrix}0\\-3\end{pmatrix}=2 \times 0 +(-2)\times (-3)=6\) ;
\(\overrightarrow{u_1}\cdot\overrightarrow{u_6} = \begin{pmatrix}1\\0\end{pmatrix} \cdot \begin{pmatrix}2\\0\end{pmatrix}=1 \times 2 +0\times 0=2\) ;
\(\overrightarrow{u_3}\cdot\overrightarrow{u_5}= \begin{pmatrix}0\\1\end{pmatrix} \cdot \begin{pmatrix}-1\\1\end{pmatrix}=0 \times (-1) +1\times 1=1\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit les vecteurs représentés ci-dessous.
Quel produit scalaire vaut 1 ?

Correction
Explication Générale
On cherche un produit scalaire positif : il faut que les deux vecteurs impliqués soient dans le même sens.
Parmi les propositions, c'est donc uniquement possible pour :\( \overrightarrow{u_2}\cdot\overrightarrow{u_4} \); \(\overrightarrow{u_1}\cdot\overrightarrow{u_6}\) et \(\overrightarrow{u_3}\cdot\overrightarrow{u_5}\).
On calcule alors ces trois produits scalaires :
\(\overrightarrow{u_2}\cdot\overrightarrow{u_4}= \begin{pmatrix}2\\-2\end{pmatrix} \cdot \begin{pmatrix}0\\-3\end{pmatrix}=2 \times 0 +(-2)\times (-3)=6\) ;
\(\overrightarrow{u_1}\cdot\overrightarrow{u_6} = \begin{pmatrix}1\\0\end{pmatrix} \cdot \begin{pmatrix}2\\0\end{pmatrix}=1 \times 2 +0\times 0=2\) ;
\(\overrightarrow{u_3}\cdot\overrightarrow{u_5}= \begin{pmatrix}0\\1\end{pmatrix} \cdot \begin{pmatrix}-1\\1\end{pmatrix}=0 \times (-1) +1\times 1=1\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Quelle doit être la norme du vecteur \(\overrightarrow{U}\) pour que le produit scalaire entre les deux vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\) soit égal à 3 ?
Données : \(\cos(60°) = \dfrac{1}{2} \)
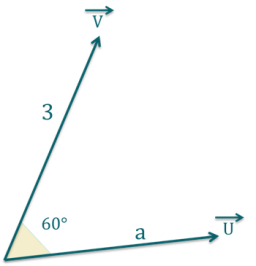
Correction
Explication Générale
Le produit scalaire de ces deux vecteurs vaut \( 3\times \cos(60) \times a\) . Pour être égal à 3, il faut donc que \(a\times \frac{1}{2} = 1\), soit \(a = 2\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Quelle doit être la norme du vecteur \(\overrightarrow{U}\) pour que le produit scalaire entre les deux vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\) soit égal à 6 ?
Données : \(\cos(60°) = \frac{1}{2}\)

Correction
Explication Générale
Le produit scalaire de ces deux vecteurs vaut \(3* \cos(60) *a\) . Pour être égal à 6, il faut donc que \(a* \frac{1}{2} = 2\), soit \(a = 4\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Le travail (en J) effectuée par une force uniforme \(\overrightarrow{F}\) (norme en N) appliquée en un solide ponctuel M, lors d'un déplacement \(\overrightarrow{l}\) (en m) est égal au produit scalaire \(\overrightarrow{F} .\overrightarrow{l}\).
On se place dans un plan muni d'un repère orthonormé \((O,\overrightarrow{i}, \overrightarrow{j})\). Le vecteur s'exprime sous la forme \(\overrightarrow{F} = F_X \overrightarrow{i} + F_Y \overrightarrow{j}\), avec \(F_X = 3\) N, \(F_y = -2\) N.
Le solide ponctuel M se déplace suivant un déplacement \(\overrightarrow{l} = l_x \overrightarrow{i} + l_y \overrightarrow{j}\), avec \(l_x = 1\) m et \(l_y = 2\) m.
Calculer le travail de \(\overrightarrow{F}\) appliquée au déplacement \(\overrightarrow{l}\).
Correction
Explication Générale
Le travail de \(\overrightarrow{F}\) appliqué au déplacement \(\overrightarrow{l}\) est défini par \(\overrightarrow{F}.\overrightarrow{l}\).
\(\overrightarrow{F}.\overrightarrow{l} = F_x . l_x + F_y . l_y = 3*1 + (-2)*2 = 3-4 = -1\) J.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Le travail (en J) effectuée par une force uniforme \(\overrightarrow{F}\) (norme en N) appliquée en un solide ponctuel M, lors d'un déplacement \(\overrightarrow{l}\) (en m) est égal au produit scalaire \(\overrightarrow{F} .\overrightarrow{l}\).
On se place dans un plan muni d'un repère \((O,\overrightarrow{i}, \overrightarrow{j})\). Le vecteur s'exprime sous la forme \(\overrightarrow{F} = F_X \overrightarrow{i} + F_Y \overrightarrow{j}\), avec \(F_X = -1\) N, \(F_y = -3\) N.
Le solide ponctuel M se déplace suivant un déplacement \(\overrightarrow{l} = l_x \overrightarrow{i} + l_y \overrightarrow{j}\), avec \(l_x = 4\) m et \(l_y = -2\) m.
Calculer le travail de \(\overrightarrow{F}\) appliquée au déplacement \(\overrightarrow{l}\) ?
Correction
Explication Générale
Le travail de \(\overrightarrow{F}\) appliqué au déplacement \(\overrightarrow{l}\) vaut \(\overrightarrow{F}.\overrightarrow{l}\).
\(\overrightarrow{F}.\overrightarrow{l} = F_x . l_x + F_y . l_y = -1*4+(-3)*(-2) = 2\) J.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
\(\overrightarrow{OA}\) et \(\overrightarrow{OB}\) sont deux vecteurs dans le plan tels que représentés sur le schéma suivant.
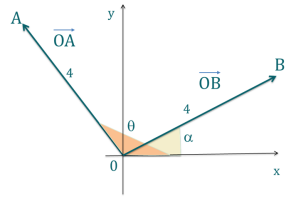
Que vaut leur produit scalaire \(\overrightarrow{OA}\cdot \overrightarrow{OB}\) ?
Correction
Explication Générale
Le produit scalaire \(\overrightarrow{OA}\cdot \overrightarrow{OB}\) est défini par \(\overrightarrow{OA} \cdot \overrightarrow{OB} = || \overrightarrow{OA} || \cdot || \overrightarrow{OB}|| \cos( (\overrightarrow{OA},\overrightarrow{OB} )) = 4\times 4 \times \cos( \theta - \alpha) = 16 \cos( \alpha - \theta)\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
\(\overrightarrow{OA}\) et \(\overrightarrow{OB}\) sont deux vecteurs dans le plan tels que représentés sur le schéma suivant.
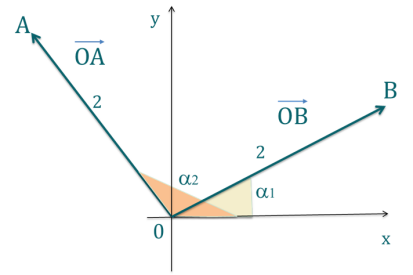
Que vaut leur produit scalaire \(\overrightarrow{OA}\cdot \overrightarrow{OB}\) ?
Correction
Explication Générale
Le produit scalaire \(\overrightarrow{OA}\cdot \overrightarrow{OB}\) est défini par \(\overrightarrow{OA} \cdot \overrightarrow{OB} = || \overrightarrow{OA} ||\cdot || \overrightarrow{OB}|| \cos( (\overrightarrow{OA},\overrightarrow{OB} )) = 2\times 2 \times \cos( \alpha_2 - \alpha_1)\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Le travail (en J) effectuée par une force \(\overrightarrow{F}\) (norme en N) appliquée en un solide ponctuel M, lors d'un déplacement \(\overrightarrow{L}\) (en m) est égal au produit scalaire \(\overrightarrow{F} .\overrightarrow{L}\).
On étudie la force \(\overrightarrow{F}\) subie par l'aile d'un avion qui subit un déplacement \(\overrightarrow{L}\).
Quelle est l'expression du travail \(W\) de cette force ?
Correction
Explication Générale
La formule du produit scalaire fait intervenir l'angle entre les deux vecteurs, ici \(\theta- \alpha\).
On a donc \(\overrightarrow{F} . \overrightarrow{L} = ||\overrightarrow{F} || . || \overrightarrow{L} || \cos(\theta - \alpha)\).
De plus, \(\cos\) est paire donc \(\cos(\theta - \alpha) = \cos(\alpha - \theta)\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Le travail (en J) effectuée par une force \(\overrightarrow{T}\) (norme en N) appliquée en un solide ponctuel M, lors d'un déplacement \(\overrightarrow{L}\) (en m) est égal au produit scalaire \(\overrightarrow{T} .\overrightarrow{L}\).
On étudie la force de traction \(\overrightarrow{T}\) subie par skieur qui subit un déplacement \(\overrightarrow{L}\).
Quelle est l'expression du travail \(W\) de cette force en fonction de \(\alpha\) et \(\theta\) ?
Correction
Explication Générale
La formule du produit scalaire fait intervenir l'angle entre les deux vecteurs, ici \(\theta- \alpha\).
On a donc \(\overrightarrow{T} . \overrightarrow{L} = ||\overrightarrow{T} || . || \overrightarrow{L} || \cos(\theta - \alpha)\).
De plus, \(\cos\) est paire donc \(\cos(\theta - \alpha) = \cos(\alpha - \theta)\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit deux vecteurs \(\overrightarrow{v_1}\) et \(\overrightarrow{v_2}\) dans l'espace, de coordonnées \(\begin{pmatrix}3\\-1\\2\end{pmatrix}\) et \(\begin{pmatrix}-1\\0\\3\end{pmatrix}\).
Que vaut le produit scalaire \(\overrightarrow{v_1}.\overrightarrow{v_2}\) ?
Correction
Explication Générale
On obtient le produit scalaire en effectuant \(\begin{pmatrix}3\\-1\\2\end{pmatrix}\cdot \begin{pmatrix}-1\\0\\3\end{pmatrix} = 3 \times (-1) + (-1) \times 0 + 2\times 3 = -3 + 6 = 3\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit deux vecteurs \(\overrightarrow{v_1}\) et \(\overrightarrow{v_2}\) dans l'espace, de coordonnées \(\begin{pmatrix}1\\-2\\4\end{pmatrix}\) et \(\begin{pmatrix}1\\-3\\0\end{pmatrix}\).
Que vaut le produit scalaire \(\overrightarrow{v_1}.\overrightarrow{v_2}\) ?
Correction
Explication Générale
On calcule le produit scalaire en effectuant \(\begin{pmatrix}1\\-2\\4\end{pmatrix}\cdot \begin{pmatrix}1\\-3\\0\end{pmatrix} = 1 \times 1 + (-2) \times (-3) + 4\times 0 = 1 + 6 = 7\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On considère les vecteurs représentés sur le schéma.
Quels sont les produits scalaires dont la valeur est égale à 2 ?
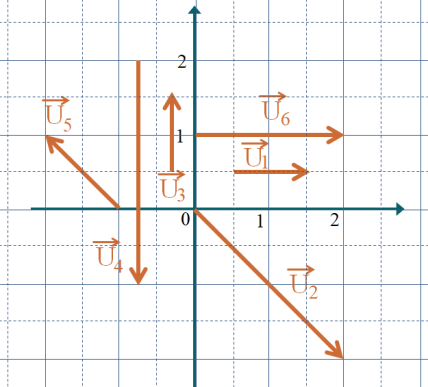
Correction
Explication Générale
On cherche un produit scalaire positif : il faut que les deux vecteurs impliqués soient dans le même sens.
Parmi les propositions, c'est donc uniquement possible pour : \( \overrightarrow{U_1}\cdot \overrightarrow{U_2}\) et \(\overrightarrow{U_1}\cdot \overrightarrow{U_6}\).
On calcule alors ces deux produits scalaires :
On lit sur le graphique les coordonnées suivantes :
\(\overrightarrow{U_1} \begin{pmatrix}1\\0\end{pmatrix}\) ; \(\overrightarrow{U_2} \begin{pmatrix}2\\-2\end{pmatrix}\) ; \(\overrightarrow{U_6} \begin{pmatrix}2\\0\end{pmatrix}\).
Comme nous sommes dans un repère orthonormé on en déduit :
\(\overrightarrow{U_1}. \overrightarrow{U_2} = 2\times 1 + (-2)\times 0 = 2\) ;
\(\overrightarrow{U_1}. \overrightarrow{U_6} = 1\times 2 + 0\times 0 = 2\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On considère les vecteurs représentés sur le schéma.
Quels sont les produits scalaires dont la valeur est égale à -2 ?

Correction
Explication Générale
On cherche un produit scalaire négatif : on cherche donc un produit scalaire entre deux vecteurs de sens opposés (l'un qui pointe vers la gauche, l'autre vers la droite). Les propositions possibles sont donc : \(\overrightarrow{U_5}\cdot \overrightarrow{U_6} \) et \( \overrightarrow{U_2}\cdot \overrightarrow{U_5}\).
On calcule alors les produits scalaires correspondants :
On lit sur le graphique les coordonnées des vecteurs :
\(\overrightarrow{U_2} \begin{pmatrix}2\\-2\end{pmatrix}\) ; \(\overrightarrow{U_5} \begin{pmatrix}-1\\1\end{pmatrix}\) ; \(\overrightarrow{U_6} \begin{pmatrix}2\\0\end{pmatrix}\).
Comme nous sommes dans un repère orthonormé on en déduit :
\(\overrightarrow{U_5}. \overrightarrow{U_6} = -1\times 2 + (1)\times 0 = -2\) ;
\(\overrightarrow{U_2}. \overrightarrow{U_5} = 2\times -1 + -2\times 1 = -4\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On considère la base \((\overrightarrow{i}, \overrightarrow{j})\) et \(a,b,c,d\) 4 nombres réels.
Soient deux forces \(\overrightarrow{F_1}= a\overrightarrow{i}+ b\overrightarrow{j}\) et \(\overrightarrow{F_2}= c\overrightarrow{i}+d\overrightarrow{j}\).
Quelle est l'expression qui permet d'obtenir les composantes du vecteur \(\overrightarrow{F_1} +\overrightarrow{F_2} \) dans la base \((\overrightarrow{i}, \overrightarrow{j})\) ?
Correction
Explication Générale
On développe la somme avec les vecteurs de base puis on factorise :
\(\overrightarrow{F_1} +\overrightarrow{F_2} = a\overrightarrow{i}+ b\overrightarrow{j} + c\overrightarrow{i}+d\overrightarrow{j} =(a+c)\overrightarrow{i}+ (b+d)\overrightarrow{j}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On considère la base \((\overrightarrow{u_x}, \overrightarrow{u_y})\) et \(a,b,c,d\) 4 nombres réels.
Soient deux forces \(\overrightarrow{F}= a\overrightarrow{u_x}+ b \overrightarrow{u_y}\) et \(\overrightarrow{T}= c\overrightarrow{u_x}+d \overrightarrow{u_y}\).
Quelle est l'expression qui permet d'obtenir les composantes du vecteur \(\overrightarrow{F} +\overrightarrow{T} \) dans la base \((\overrightarrow{u_x}, \overrightarrow{u_y})\) ?
Correction
Explication Générale
\(\overrightarrow{F} +\overrightarrow{T} = a\overrightarrow{u_x}+ b \overrightarrow{u_y} + c\overrightarrow{u_x}+d \overrightarrow{u_y} =(a+c)\overrightarrow{u_x}+ (b+d) \overrightarrow{u_y}\)
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On considère la base \((\overrightarrow{i}, \overrightarrow{j})\) et \(a,b,c,d\) 4 nombres réels.
Soient deux vecteurs \(\overrightarrow{AB}= a\overrightarrow{i}+ b\overrightarrow{j}\) et \(\overrightarrow{BC}= c\overrightarrow{i}+d\overrightarrow{j}\).
Quel vecteur est correctement exprimé dans la base dans la base \((\overrightarrow{i}, \overrightarrow{j})\) ?
Correction
Explication Générale
\(\overrightarrow{AC}= \overrightarrow{AB}+\overrightarrow{BC}\) et \(\overrightarrow{CA}=-\overrightarrow{AC}\)
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On considère la base \((\overrightarrow{i}, \overrightarrow{j})\) et \(a,b,c,d\) 4 nombres réels.
Soient deux vecteurs forces \(\overrightarrow{F_1}= a\overrightarrow{i}+ b\overrightarrow{j}\) et \(\overrightarrow{F_2}= c\overrightarrow{i}+d\overrightarrow{j}\).
Quel vecteur est correctement exprimé dans la base dans la base \((\overrightarrow{i}, \overrightarrow{j})\) ?
Correction
Explication Générale
\(\overrightarrow{F_1}+\overrightarrow{F_2}= (a+c)\overrightarrow{i}+ (b+d)\overrightarrow{j} =(a+c)\overrightarrow{i}+ (b+d)\overrightarrow{j}\)
et \(-\overrightarrow{F_1}-\overrightarrow{F_2}= -(a\overrightarrow{i}+ b\overrightarrow{j})-(c\overrightarrow{i}+ d\overrightarrow{j}) =-(a+c)\overrightarrow{i}+ -(b+d)\overrightarrow{j}\)
?Exprimer une grandeur à partir de plusieurs relations
Énoncé
On désigne par \(\begin{pmatrix}x\\y\end{pmatrix}\) et \(\begin{pmatrix}x'\\y'\end{pmatrix}\) les coordonnées dans la base (\(\overrightarrow{i}\), \(\overrightarrow{j}\)) de deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\).
Quelles relations doivent vérifier les nombres réels \(x,y,x',y'\) pour que \(\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{0}\) ?
Correction
Explication Générale
\(\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{0}\) si toutes les coordonnées du vecteurs \(\overrightarrow{u}+\overrightarrow{v}\) sont nulles, c'est-à-dire si \(x+x'=0\) et si \(y+y'=0\).
?Exprimer une grandeur à partir de plusieurs relations
Énoncé
On désigne par \(\begin{pmatrix}x\\y\end{pmatrix}\) et \(\begin{pmatrix}x'\\y'\end{pmatrix}\) les coordonnées dans la base (\(\overrightarrow{i}\), \(\overrightarrow{j}\)) de deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\).
Quelles relations doivent vérifier les nombres réels \(x,y,x',y'\) pour que \(2\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{0}\) ?
Correction
Explication Générale
\(2\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{0}\) si toutes les coordonnées du vecteurs \(2\overrightarrow{u}+\overrightarrow{v}\) sont nulles c'est-à-dire si \(2x+x'=0\) et si \(2y+y'=0\).
?Exprimer une grandeur à partir de plusieurs relations
Énoncé
On désigne par \(\begin{pmatrix}x\\y\end{pmatrix}\) et \(\begin{pmatrix}x'\\y'\end{pmatrix}\) les coordonnées dans la base \((\overrightarrow{i}, \overrightarrow{j})\) de deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\).
Quelles relations doivent vérifier les nombres réels \(x,y,x',y'\) pour que \(\overrightarrow{u}-\overrightarrow{v}=\overrightarrow{0}\) ?
Correction
Explication Générale
\(\overrightarrow{u}-\overrightarrow{v}=\overrightarrow{0}\) si toutes les coordonnées du vecteurs \(\overrightarrow{u}-\overrightarrow{v}\) sont nulles c'est-à-dire si \(x-x'=0\) et \(y-y'=0\).
?Exprimer une grandeur à partir de plusieurs relations
Énoncé
On désigne par \(\begin{pmatrix}x\\y\end{pmatrix}\) et \(\begin{pmatrix}x'\\y'\end{pmatrix}\) les coordonnées dans la base \((\overrightarrow{i}, \overrightarrow{j})\) de deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\).
Quelles relations doivent vérifier les nombres réels \(x,y,x',y'\) pour que \(\overrightarrow{u}-2\overrightarrow{v}=\overrightarrow{0}\) ?
Correction
Explication Générale
\(\overrightarrow{u}-2\overrightarrow{v}=\overrightarrow{0}\) si toutes les coordonnées du vecteurs \(\overrightarrow{u}-2\overrightarrow{v}\) sont nulles c'est-à-dire \(x-2x'=0\) et \(y-2y'=0\).
?Exprimer une grandeur à partir de plusieurs relations
Énoncé
Soit \(\overrightarrow{u}\) et \(\overrightarrow{v}\) de coordonnées respectives dans \(R^2\) \(\begin{pmatrix}2a\\-3\end{pmatrix}\) et \(\begin{pmatrix}1\\b\end{pmatrix}\).
\(a\) et \(b\) étant des nombres réels.
Quel couple de valeurs \((a,b)\) permet d'obtenir que la somme des vecteurs soit le vecteur nul \(\overrightarrow{0}\) ?
Correction
Explication Générale
\(\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{0}\) si toutes les coordonnées du vecteurs \(\overrightarrow{u}+\overrightarrow{v}\) sont nulles c'est-à-dire \(2a+1=0\) et \(-3+b=0\).
Ainsi la somme des vecteurs est nulle si \(a=0,5\) et \(b=3\).
?Exprimer une grandeur à partir de plusieurs relations
Énoncé
Soit \(\overrightarrow{u}\) et \(\overrightarrow{v}\) de coordonnées respectives dans \(R^2\) \(\begin{pmatrix}3a\\-2\end{pmatrix}\) et \(\begin{pmatrix}-6\\2b\end{pmatrix}\).
\(a\) et \(b\) étant des nombres réels.
Quel couple de valeurs \((a,b)\) permet d'obtenir que la somme des vecteurs soit le vecteur nul \(\overrightarrow{0}\) ?
Correction
Explication Générale
\(\overrightarrow{u}+\overrightarrow{v}=\overrightarrow{0}\) si toutes les coordonnées du vecteurs \(\overrightarrow{u}+\overrightarrow{v}\) sont nulles c'est-à-dire \(3a-6=0\) et \(-2+2b=0\).
Ainsi la somme des vecteurs est nulle si \(a=2\) et \(b=1\).
?Exprimer une grandeur à partir de plusieurs relations
Énoncé
Soit \(\overrightarrow{u}, \overrightarrow{v}\) et \(\overrightarrow{w}\) de coordonnées respectives dans \(R^3\) \(\begin{pmatrix}2\\3a\\-b\end{pmatrix}\),\(\begin{pmatrix}a\\2b\\0\end{pmatrix}\) et \(\begin{pmatrix}0\\2a\\b\end{pmatrix}\), \(a\) et \(b\) étant des nombres réels.
Quelles valeurs de \(a\) et de \(b \) permettent d'obtenir que la somme des vecteurs soit le vecteur nul \(\overrightarrow{0}\) ?
Correction
Explication Générale
Le plus simple pour répondre à cette question est de substituer les valeurs proposées.
Méthode de résolution générale :
La relation \(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}=\overrightarrow{0}\) est vérifiée si toutes les coordonnées du vecteurs \(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}\) sont nulles c'est-à-dire si \(\begin{pmatrix}2\\3\times a\\-b\end{pmatrix}+ \begin{pmatrix}a\\2\times b\\0\end{pmatrix} + \begin{pmatrix}0\\2\times a\\+b\end{pmatrix} = \begin{pmatrix}0\\0\\0\end{pmatrix}\).
Cela revient à résoudre les équations suivantes : \(2+a+0=0\), \(3a+2b+2a=0\) et \(-b+0+b=0\).
Soit \(2+a=0\) et \(5a+2b=0\) \(\iff{}\) \(2b=-5a\).
Ainsi la somme des vecteurs est nulle si \(a=-2\) et \(b=5\).
?Exprimer une grandeur à partir de plusieurs relations
Énoncé
Soit \(\overrightarrow{u}, \overrightarrow{v}\) et \(\overrightarrow{w}\) de coordonnées respectives dans \(R^3\) \(\begin{pmatrix}2\\a\\-b\end{pmatrix}\),\(\begin{pmatrix}2a\\b\\0\end{pmatrix}\) et \(\begin{pmatrix}0\\-2a\\b\end{pmatrix}\), \(a\) et \(b\) étant des nombres réels.
Quel couple de valeurs \((a,b)\) permet d'obtenir que la somme des vecteurs soit le vecteur nul \(\overrightarrow{0}\) ?
Correction
Explication Générale
Le plus simple pour répondre à cette question est de substituer les valeurs proposées.
Méthode de résolution générale :
La relation \(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}=\overrightarrow{0}\) est vérifiée si toutes les coordonnées du vecteurs \(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}\) sont nulles c'est-à-dire si \(\begin{pmatrix}2\\a\\-b\end{pmatrix}+ \begin{pmatrix}2\timesa\\b\\0\end{pmatrix} + \begin{pmatrix}0\\-2\times a\\+b\end{pmatrix} = \begin{pmatrix}0\\0\\0\end{pmatrix}\).
Cela revient à résoudre les équations suivantes : \(2+2a+0=0\), \(a+b-2a=0\) et \(-b+0+b=0\).
Soit \(2+2a=0\) et \(b-a=0\) \(\iff{}\) \(b=a\).
Ainsi la somme des vecteurs est nulle si \(a=-1\) et \(b=-1\).
?Exprimer une grandeur à partir de plusieurs relations
Énoncé
Soient un mobile soumis à trois forces \(\overrightarrow{P}, \overrightarrow{F}\) et \(\overrightarrow{T}\) de coordonnées respectives dans le repère \((0,\overrightarrow {i}, \overrightarrow {j}) : \overrightarrow {P} : \begin{pmatrix}0\\2a\end{pmatrix}, \overrightarrow {F} : \begin{pmatrix}-2\\3\end{pmatrix}\) et \(\overrightarrow {T} : \begin{pmatrix}a\\b\end{pmatrix}\)
\(a\) et \(b\) étant deux nombres réels.
Quel couple de valeurs \((a,b)\) permet d'obtenir que le vecteur résultant \(\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}\) soit le vecteur nul \(\overrightarrow{0}\) ?
Correction
Explication Générale
Le plus simple est d'essayer les valeurs proposées par substitution.
Méthode de résolution générale
La relation \(\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}=\overrightarrow{0}\) est vraie si toutes les coordonnées du vecteurs \(\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}\) sont nulles c'est-à-dire si \(\begin{pmatrix}0\\2\times a\end{pmatrix}+ \begin{pmatrix}-2\\3\end{pmatrix} + \begin{pmatrix}a\\b\end{pmatrix} = \begin{pmatrix}0\\0\end{pmatrix}\).
Cela revient à résoudre les équations suivantes : \(0-2+a=0\) et\(2a+3+b=0\).
Soit \(a=2\) et \(b=-2a-3\).
Ainsi la somme des vecteurs est nulle si \(a=2\) et \(b=-7\).
?Exprimer une grandeur à partir de plusieurs relations
Énoncé
Soient un mobile soumis à trois forces \(\overrightarrow{P}, \overrightarrow{F}\) et \(\overrightarrow{T}\) de coordonnées respectives dans le repère \((0,\overrightarrow {i}, \overrightarrow {j}) : \overrightarrow {P} : \begin{pmatrix}0\\a\end{pmatrix}\), \(\overrightarrow {F} : \begin{pmatrix}5\\-1\end{pmatrix}\)et \(\overrightarrow {T} : \begin{pmatrix}a\\b\end{pmatrix}\).
\(a\) et \(b\) étant deux nombres réels.
Quel couple de valeurs \((a,b)\) permet d'obtenir que le vecteur résultant \(\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}\) soit le vecteur nul \(\overrightarrow{0}\) ?
Correction
Explication Générale
Le plus simple est d'essayer les valeurs proposées par substitution.
Méthode de résolution générale
La relation \(\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}=\overrightarrow{0}\) est vraie si toutes les coordonnées du vecteurs \(\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}\) sont nulles c'est-à-dire si \(\begin{pmatrix}0\\a\end{pmatrix}+ \begin{pmatrix}5\\-1\end{pmatrix} + \begin{pmatrix}a\\b\end{pmatrix} = \begin{pmatrix}0\\0\end{pmatrix}\).
Cela revient à résoudre les équations suivantes : \(0+5+a=0\) et\(a-1+b=0\).
Soit \(a=-5\) et \(b=-a+1\).
Ainsi la somme des vecteurs est nulle si \(a=2\) et \(b=-6\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On se place dans \(R^3\), avec un repère orthonormé et trois axes \((Ox, Oy, Oz)\).
On considère \(\overrightarrow{u}\) de coordonnées \(\begin{pmatrix}2\\5\\-1\end{pmatrix}\) et \(\overrightarrow{v}\) de coordonnées \(\begin{pmatrix}-1\\-2\\3\end{pmatrix}\).
Lesquels de ces vecteurs ont une coordonnée positive suivant \(Oy\) ?
Correction
Explication Générale
Pour résoudre cet exercice on utilise deux propriétés :
La coordonnée selon \(y\) de \(\overrightarrow{u}+\overrightarrow{v}\) est égale à la somme des coordonnées selon \(y\) de \(\overrightarrow{u}\) et de \(\overrightarrow{v}\) : \(u_y+v_y\).
La coordonnée selon \(y\) de \(a\overrightarrow{u}\) est égale à \(a\) fois la coordonnée selon \( y\) de \(\overrightarrow{u}\) : \(a\cdot u_y\).
Bonnes réponses :
La coordonnée de \(2 \overrightarrow{u} + \overrightarrow{v}\) suivant l'axe \(Oy\) vaut \(2\times 5 -2 = 8\). Elle est bien strictement positive.
La coordonnée de \(\overrightarrow{u} - 2 \overrightarrow{v}\) suivant l'axe \(Oy\) vaut \(5 -2 \times (-2) = 9\). Elle est bien strictement positive.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On se place dans \(R^3\), avec un repère orthonormé et trois axes \((Ox, Oy, Oz)\).
On considère \(\overrightarrow{u}\) de coordonnées \(\begin{pmatrix}2\\5\\-1\end{pmatrix}\) et \(\overrightarrow{v}\) de coordonnées \(\begin{pmatrix}-1\\-2\\3\end{pmatrix}\).
Lesquels de ces vecteurs ont une coordonnée positive suivant \(Oz\) ?
Correction
Explication Générale
Pour résoudre cet exercice on utilise deux propriétés :
La coordonnée selon \(z\) de \(\overrightarrow{u}+\overrightarrow{v}\) est égale à la somme des coordonnées selon \(z\) de \(\overrightarrow{u}\) et de \(\overrightarrow{v}\) : \(u_z+v_z\).
La coordonnée selon \(z\) de \(a\overrightarrow{u}\) est égale à \(a\) fois la coordonnée selon \( z\) de \(\overrightarrow{u}\) : \(a\cdot u_z\).
Bonnes réponses
La coordonnée de \(2 \overrightarrow{u} + \overrightarrow{v}\) suivant l'axe \(Oz\) vaut \(2*(-1) +3 = 1\). Elle est strictement positive.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On se place dans \(R^3\), avec un repère orthonormé et trois axes \((Ox, Oy, Oz)\).
On considère \(\overrightarrow{u}\) de coordonnées \(\begin{pmatrix}2\\5\\-1\end{pmatrix}\) et \(\overrightarrow{v}\) de coordonnées \(\begin{pmatrix}-1\\-2\\3\end{pmatrix}\).
Lesquels de ces vecteurs ont une coordonnée strictement positive suivant \(Ox\) ?
Correction
Explication Générale
Pour résoudre cet exercice on utilise deux propriétés :
La coordonnée selon \(x\) de \(\overrightarrow{u}+\overrightarrow{v}\) est égale à la somme des coordonnées selon \(x\) de \(\overrightarrow{u}\) et de \(\overrightarrow{v}\) : \(u_x+v_x\).
La coordonnée selon \(x\) de \(a\overrightarrow{u}\) est égale à \(a\) fois la coordonnée selon \( x\) de \(\overrightarrow{u}\) : \(a\cdot u_x\).
Bonnes réponses
La coordonnée de \(2 \overrightarrow{u} + \overrightarrow{v}\) suivant l'axe \(Ox\) vaut \(2\times 2 -1 = 3\). Elle est strictement positive.
La coordonnée de \(\overrightarrow{u} - 2 \overrightarrow{v}\) suivant l'axe \(Ox\) vaut \(2 -2 \times (-1) = 4\). Elle est strictement positive.
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) de \(R^3\) de coordonnées respectives \(\begin{pmatrix}2\\-3\\1\end{pmatrix}\) et \(\begin{pmatrix}1\\2\\-3\end{pmatrix}\).
Quelles sont les coordonnées du vecteur \(\overrightarrow{u} + \overrightarrow{v}\) ?
Correction
Explication Générale
Les coordonnées du vecteur \(\overrightarrow{u} + \overrightarrow{v}\) sont : \(\begin{pmatrix}u_x+v_x\\u_y+v_y\\u_z+v_z\end{pmatrix}\) avec \(u_x\), \(u_y\), \(u_z\), \(v_x\), \(v_y\) et \(v_z\) les coordonnées des vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) selon les axes \(Ox\), \(Oy\) et \(Oz\).
Ainsi les coordonnées de ce vecteur sont : \(\begin{pmatrix}2\\-3\\1\end{pmatrix}+\begin{pmatrix}1\\2\\-3\end{pmatrix}=\begin{pmatrix}2+1\\-3+2\\1-3\end{pmatrix}\) donc les coordonnées sont : \(\begin{pmatrix}3\\-1\\-2\end{pmatrix}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) de \(R^3\) de coordonnées respectives \(\begin{pmatrix}1\\-2\\-3\end{pmatrix}\) et \(\begin{pmatrix}-1\\3\\2\end{pmatrix}\).
Quelles sont les coordonnées du vecteur \(\overrightarrow{u} + \overrightarrow{v}\) ?
Correction
Explication Générale
Les coordonnées du vecteur \(\overrightarrow{u} + \overrightarrow{v}\) sont : \(\begin{pmatrix}u_x+v_x\\u_y+v_y\\u_z+v_z\end{pmatrix}\) avec \(u_x\), \(u_y\), \(u_z\), \(v_x\), \(v_y\) et \(v_z\) les coordonnées des vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) selon les axes \(Ox\), \(Oy\) et \(Oz\).
Ainsi les coordonnées de ce vecteurs sont : \(\begin{pmatrix}1\\-2\\-3\end{pmatrix}+\begin{pmatrix}-1\\3\\2\end{pmatrix}=\begin{pmatrix}1-1\\-2+3\\-3+2\end{pmatrix}\) donc les coordonnées sont : \(\begin{pmatrix}0\\1\\-1\end{pmatrix}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) de \(R^3\) de coordonnées respectives \(\begin{pmatrix}4\\1\\-2\end{pmatrix}\) et \(\begin{pmatrix}-2\\0\\1\end{pmatrix}\).
Quelles sont les coordonnées du vecteur \(\overrightarrow{u} - \overrightarrow{v}\) ?
Correction
Explication Générale
Les coordonnées du vecteur \(\overrightarrow{u} - \overrightarrow{v}\) sont : \(\begin{pmatrix}u_x-v_x\\u_y-v_y\\u_z-v_z\end{pmatrix}\) avec \(u_x\), \(u_y\), \(u_z\), \(v_x\), \(v_y\) et \(v_z\) les coordonnées des vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) selon les axes \(Ox\), \(Oy\) et \(Oz\).
Ainsi les coordonnées de ce vecteurs sont : \(\begin{pmatrix}4\\1\\-2\end{pmatrix}-\begin{pmatrix}-2\\0\\1\end{pmatrix}=\begin{pmatrix}4-(-2)\\1-0\\-2-1\end{pmatrix}\) donc les coordonnées sont : \(\begin{pmatrix}6\\1\\-3\end{pmatrix}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit deux vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) de \(R^3\) de coordonnées respectives \(\begin{pmatrix}3\\1\\-4\end{pmatrix}\) et \(\begin{pmatrix}-2\\0\\3\end{pmatrix}\).
Quelles sont les coordonnées du vecteur \(\overrightarrow{u} - \overrightarrow{v}\) ?
Correction
Explication Générale
Les coordonnées du vecteur \(\overrightarrow{u} - \overrightarrow{v}\) sont : \(\begin{pmatrix}u_x-v_x\\u_y-v_y\\u_z-v_z\end{pmatrix}\) avec \(u_x\), \(u_y\), \(u_z\), \(v_x\), \(v_y\) et \(v_z\) les coordonnées des vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) selon les axes \(Ox\), \(Oy\) et \(Oz\).
Ainsi les coordonnées de ce vecteurs sont : \(\begin{pmatrix}3\\1\\-4\end{pmatrix}-\begin{pmatrix}-2\\0\\3\end{pmatrix}=\begin{pmatrix}3-(-2)\\1-0\\-4-3\end{pmatrix}\) donc les coordonnées sont : \(\begin{pmatrix}5\\1\\-7\end{pmatrix}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient deux vecteurs \(\overrightarrow{u}, et \overrightarrow{v}\) tels que \(\overrightarrow{u} = \begin{pmatrix}4\\1\\-2\end{pmatrix}\) et \(\overrightarrow{v} = \begin{pmatrix}-2\\0\\1\end{pmatrix}\).
Quelles sont les coordonnées du vecteur \(\overrightarrow{u} - \overrightarrow{v}\) ?
Correction
Explication Générale
Les coordonnées du vecteur \(\overrightarrow{u} - \overrightarrow{v}\) sont : \(\begin{pmatrix}u_x-v_x\\u_y-v_y\\u_z-v_z\end{pmatrix}\) avec \(u_x\), \(u_y\), \(u_z\), \(v_x\), \(v_y\) et \(v_z\) les coordonnées des vecteurs \(\overrightarrow{u}\) et \(\overrightarrow{v}\) selon les axes \(Ox\), \(Oy\) et \(Oz\).
Ainsi les coordonnées de ce vecteurs sont : \(\begin{pmatrix}4\\1\\-2\end{pmatrix}-\begin{pmatrix}-2\\0\\1\end{pmatrix}=\begin{pmatrix}4-(-2)\\1-0\\-2-1\end{pmatrix}\) donc les coordonnées sont : \(\begin{pmatrix}6\\1\\-3\end{pmatrix}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit deux vecteurs \(\overrightarrow{u}\) et\(\overrightarrow{v}\) dans \(R^3\) tels que \(\overrightarrow{u}\) a pour cooordonnées \(\begin{pmatrix}3\\-1\\2\end{pmatrix}\) et \(\overrightarrow{u} + \overrightarrow{v}\) a pour coordonnées \(\begin{pmatrix}2\\-2\\3\end{pmatrix}\).
Quelles sont les coordonnées de \(\overrightarrow{v}\) ?
Correction
Explication Générale
D'après l'énoncé on sait que : \(\overrightarrow{u} + \overrightarrow{v} = \begin{pmatrix}2\\-2\\3\end{pmatrix}\).
On peut donc isoler \(\overrightarrow{v}\) ce qui donne : \( \overrightarrow{v} = \begin{pmatrix}2\\-2\\3\end{pmatrix} - \overrightarrow{u}\).
Application numérique : \(\overrightarrow{v}= \begin{pmatrix}2\\-2\\3\end{pmatrix} - \begin{pmatrix}3\\-1\\2\end{pmatrix} = \begin{pmatrix}2-3\\-2-(-1)\\3-2\end{pmatrix}\).
On a donc pour finir : \(\overrightarrow{v}= \begin{pmatrix}-1\\-1\\1\end{pmatrix}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
D'après le graphique suivant, quelles sont les coordonnées dans \(R^2\) du vecteur \(\overrightarrow{U} + \overrightarrow{V}\) ?
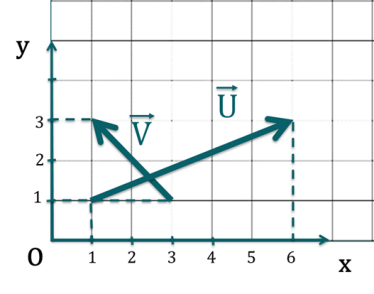
Correction
Explication Générale
Raisonnement : Deux options pour résoudre cet exercice :
Soit on construit graphiquement le vecteur somme, et ensuite on lit les coordonnées du vecteur somme.
Soit on lit les coordonnées de chaque vecteur et ensuite on fait la somme.
Calcul en suivant la deuxième méthode :
D'après le graphique , \(\overrightarrow{U} = 5\overrightarrow{u_x}+2\overrightarrow{u_y}\) et \(\overrightarrow{V} = -2\overrightarrow{u_x}+2\overrightarrow{u_y}\).
La somme des deux vecteurs vaut donc \(\overrightarrow{U} + \overrightarrow{V}=(5-2)\overrightarrow{u_x}+(2+2)\overrightarrow{u_y}=3\overrightarrow{u_x}+4\overrightarrow{u_y}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
D'après le graphique suivant, quelles sont les coordonnées dans \(R^2\) du vecteur \(\overrightarrow{U} - \overrightarrow{V}\) ?

Correction
Explication Générale
Raisonnement : Deux options pour résoudre cet exercice :
Soit on construit graphiquement le vecteur différence, et ensuite on lit ses coordonnées.
Soit on lit les coordonnées de chaque vecteur et ensuite on fait la différence.
Calcul en suivant la deuxième méthode :
D'après le graphique , \(\overrightarrow{U} = 5\overrightarrow{u_x}+2\overrightarrow{u_y}\) et \(\overrightarrow{V} = -2\overrightarrow{u_x}+2\overrightarrow{u_y}\).
La différence des deux vecteurs vaut donc \(\overrightarrow{U} + \overrightarrow{V}=(5+2)\overrightarrow{u_x}+(2-2)\overrightarrow{u_y}=7\overrightarrow{u_x}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On se place dans \(R^2\), avec un repère orthonormé et deux axes \((Ox, Oy)\).
Deux forces \(\overrightarrow{F_1}\) de norme 60 N et \(\overrightarrow{F_2}\) de norme 40 N s'exercent sur un corps au même point d'application M.
Quelles sont les coordonnées du vecteur \(\overrightarrow{F}\) résultant \(\overrightarrow{F_1}+\overrightarrow{F_2}\) ?
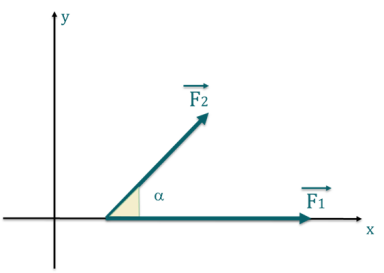
Correction
Explication Générale
Raisonnement : On décompose d'abord chaque vecteur dans la base \((\overrightarrow{u_x},\overrightarrow{u_y})\) pour ensuite sommer les composantes de chaque vecteur.
Calcul : Le vecteur \(\overrightarrow{F_1}\) est selon \(\overrightarrow{u_x}\) uniquement, on a donc : \(\overrightarrow{F_1}=60\overrightarrow{u_x}\).
Pour projeter le vecteur \(\overrightarrow{F_2}\), on utilise le triangle rectangle dessiné sur la figure ci-dessous. On a donc \(\overrightarrow{F_2}=40 \cos(\alpha)\ \overrightarrow{u_x}+ 40 \sin(\alpha)\ \overrightarrow{u_y}\).
La somme vectorielle donne \(\overrightarrow{F}= \left(60 + 40 \cos(\alpha)\right)\overrightarrow{u_x} +40 \sin(\alpha)\ \overrightarrow{u_y}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On se place dans \(R^2\), avec un repère orthonormé et deux axes \((Ox, Oy)\).
Deux forces \(\overrightarrow{F_1}\) de norme 100 N et \(\overrightarrow{F_2}\) de norme 50 N s'exercent sur un corps au même point d'application M.
Quelles sont les composantes du vecteur \(\overrightarrow{F}\) résultant \(\overrightarrow{F_1}+\overrightarrow{F_2}\) ?
Correction
Explication Générale
Raisonnement : On décompose d'abord chaque vecteur dans la base \((\overrightarrow{u_x},\overrightarrow{u_y})\) pour ensuite sommer les composantes de chaque vecteur.
Calcul : Pour projeter le vecteur \(\overrightarrow{F_1}\), on utilise le triangle rectangle dessiné sur la figure ci-dessous. On a donc \(\overrightarrow{F_1}=-100 \cos(\alpha)\ \overrightarrow{u_x}+ \left(50-100 \sin(\alpha)\right)\overrightarrow{u_y}\).
Le vecteur \(\overrightarrow{F_2}\) est selon \(\overrightarrow{u_y}\) uniquement, on a donc : \(\overrightarrow{F_1}=50\overrightarrow{u_y}\).
La somme vectorielle donne \(\overrightarrow{F}= \left(-100 \cos{\alpha}\right)\overrightarrow{u_x} +\left(50 -100 * \sin{\alpha})\right)\overrightarrow{u_y}\).
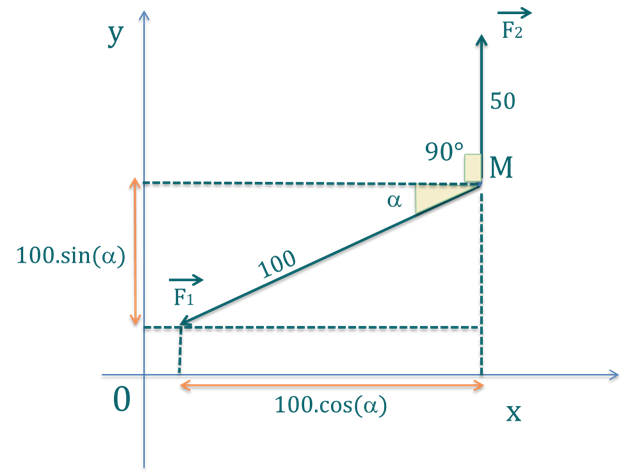
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient deux vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\).
Dans quel(s) cas a-t-on la relation \(\overrightarrow{U}+\overrightarrow{V}=\overrightarrow{0}\) ?
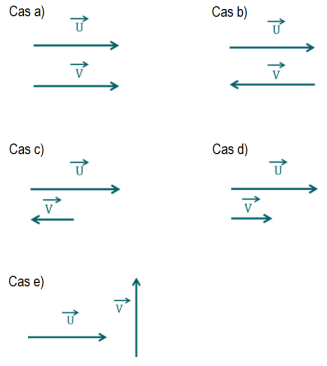
Correction
Explication Générale
Pour que la somme de deux vecteurs soit égale au vecteur nul il faut qu'ils aient :
la même direction ;
la même norme ;
des sens opposés.
Résolution graphique :
\(\overrightarrow{U}+\overrightarrow{V}=\overrightarrow{0}\) correspond à la représentation graphique suivante :
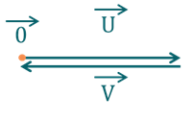
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient deux vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\).
Quelle représentation vérifie \(\overrightarrow{U}+2\overrightarrow{V}=\overrightarrow{0}\) ?
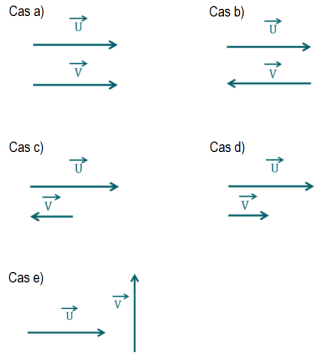
Correction
Explication Générale
Pour que la somme de deux vecteurs soit égale au vecteur nul il faut qu'ils aient :
la même direction ;
la même norme ;
des sens opposés.
Résolution graphique :
La relation \(\overrightarrow{U}+2\overrightarrow{V}=\overrightarrow{0}\) correspond à la représentation graphique suivante :
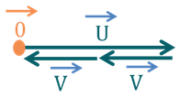
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient deux vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\).
Quelle représentation vérifie \(\overrightarrow{U}-\overrightarrow{V}=\overrightarrow{0}\) ?
Correction
Explication Générale
Pour que la différence de deux vecteurs soit égale au vecteur nul il faut qu'ils aient :
- La même direction
- La même norme
- Les mêmes sens
Résolution graphique :
La relation \(\overrightarrow{U}-\overrightarrow{V}=\overrightarrow{0}\) correspond à la représentation graphique :
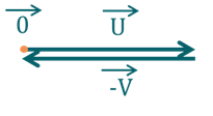
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient deux vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\).
Quelle représentation vérifie \(\overrightarrow{U}-2\overrightarrow{V}=\overrightarrow{0}\) ?
Correction
Explication Générale
Pour que la différence de deux vecteurs soit égale au vecteur nul il faut qu'ils aient :
la même direction ;
la même norme ;
les mêmes sens.
Résolution graphique :
La relation \(\overrightarrow{U}-2\overrightarrow{V}=\overrightarrow{0}\) correspond à la représentation graphique :
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit une rivière dont la vitesse du courant est représentée par \(\overrightarrow{U}\). Un nageur traverse la rivière en nageant à la vitesse \(\overrightarrow{V}\) perpendiculairement au courant.
Quelle est la représentation du vecteur vitesse du nageur \(\overrightarrow{W}\) sachant que \(\overrightarrow{W}= \overrightarrow{U}+ \overrightarrow{V}\) ?
Correction
Explication Générale
On veut obtenir la représentation du vecteur \(\overrightarrow{W}\) sachant que \(\overrightarrow{W}= \overrightarrow{U}+ \overrightarrow{V}\).
Pour cela, on place en priorité le vecteur \(\overrightarrow{U}\) puis on place à sa suite le vecteur \(\overrightarrow{V}\).
Le vecteur \(\overrightarrow{W}\) est alors représenté entre le début de la flèche du vecteur \(\overrightarrow{U}\) et de la fin de celle du vecteur \(\overrightarrow{V}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit une rivière dont la vitesse du courant est représentée par \(\overrightarrow{U}\). Un nageur traverse la rivière en nageant à la vitesse \(\overrightarrow{V}\) perpendiculairement au courant.
Quelle est la représentation du vecteur déplacement du nageur \(\overrightarrow{W}\) sachant que \(\overrightarrow{W}= \overrightarrow{U}+ \overrightarrow{V}\) ?
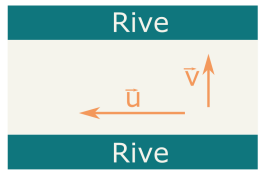
Correction
Explication Générale
On veut obtenir la représentation du vecteur \(\overrightarrow{W}\) sachant que \(\overrightarrow{W}= \overrightarrow{U}+ \overrightarrow{V}\).
Pour cela, on place en priorité le vecteur \(\overrightarrow{U}\) puis on place à sa suite le vecteur \(\overrightarrow{V}\).
Le vecteur \(\overrightarrow{W}\) est alors représenté entre le début de la flèche du vecteur \(\overrightarrow{U}\) et de la fin de celle du vecteur \(\overrightarrow{V}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit une rivière dont la vitesse du courant est représentée par \(\overrightarrow{U}\). Un nageur traverse la rivière en nageant à la vitesse \(\overrightarrow{V}\) perpendiculairement au courant.
Quelle est la représentation du vecteur déplacement du nageur \(\overrightarrow{W}\) sachant que \(\overrightarrow{W}= \overrightarrow{U}+ \overrightarrow{V}\) ?
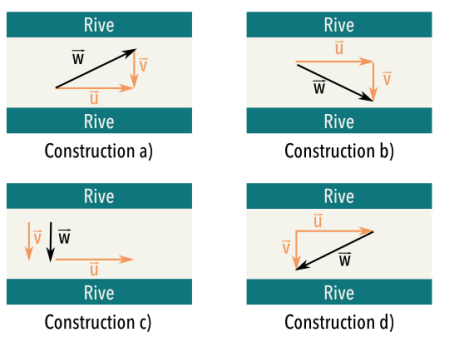
Correction
Explication Générale
Le vecteur \(\overrightarrow{W}\) est la somme des vecteurs \(\overrightarrow{U}\) et \(\overrightarrow{V}\). La construction géométrique se fait en mettant le point de départ du vecteur \(\overrightarrow{V}\) au niveau du point d'arrivée du vecteur \(\overrightarrow{U}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit une rivière dont la vitesse du courant est représentée par \(\overrightarrow{U}\). Un nageur traverse la rivière en nageant à la vitesse \(\overrightarrow{V}\) perpendiculairement au courant.
Quelle est la représentation du vecteur déplacement du nageur \(\overrightarrow{W}\) sachant que \(\overrightarrow{W}= \overrightarrow{U}+ \overrightarrow{V}\) ?
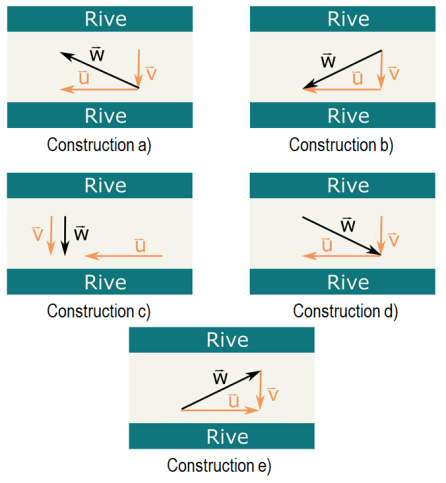
Correction
Explication Générale
On veut obtenir la représentation du vecteur \(\overrightarrow{W}\) sachant que \(\overrightarrow{W}= \overrightarrow{U}+ \overrightarrow{V}\).
Pour cela, on place en priorité le vecteur \(\overrightarrow{U}\) puis on place à sa suite le vecteur \(\overrightarrow{V}\).
Le vecteur \(\overrightarrow{W}\) est alors représenté entre le début de la flèche du vecteur \(\overrightarrow{U}\) et de la fin de celle du vecteur \(\overrightarrow{V}\).
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soient trois vecteurs : \(\overrightarrow{U}, \overrightarrow{V}\) et \(\overrightarrow{W}\).
Laquelle des affirmations suivantes est vraie ?
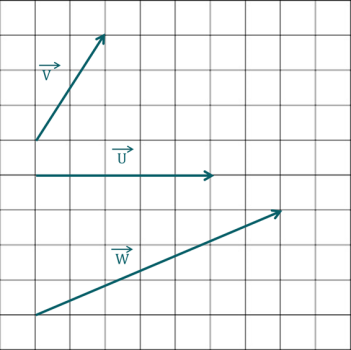
Correction
Explication Générale
Graphiquement :
Il faut voir les vecteurs comme des déplacements dans le plan. Additionner deux vecteurs c'est se déplacer du premier vecteur, puis du deuxième.
Pour additionner deux vecteurs on met le début du deuxième vecteur à la fin du premier vecteur. Le vecteur somme relie le point de départ et le point d'arrivée :
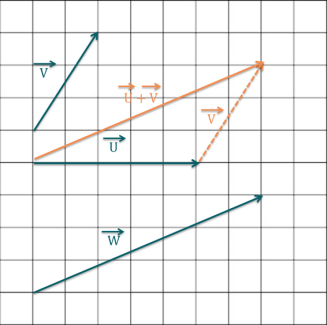
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Parmi les vecteurs "somme” suivants, lequel a la plus grande norme ?
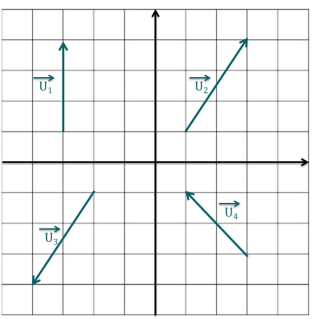
Correction
Explication Générale
La norme correspond à la longueur du vecteur. Pour répondre à la question il faut faire chaque somme graphiquement puis comparer les normes obtenues.
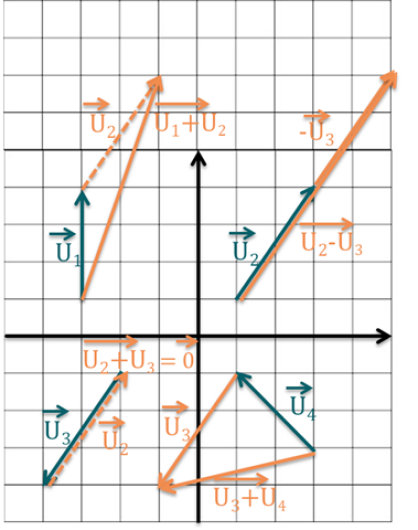
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
On construit des vecteurs résultants en sommant des vecteurs pris sur le graphique ci-dessous.
Parmi les vecteurs "somme” suivants, lequel a la plus petite norme ?

Correction
Explication Générale
La norme correspond à la longueur du vecteur. Pour répondre à la question il faut faire chaque somme graphiquement puis comparer les normes obtenues.

?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Un objet ponctuel peut être soumis à plusieurs forces présentées dans le schéma ci-dessous.
Parmi les propositions suivantes, quelle(s) combinaison(s) de forces tire le plus l'objet vers la droite ?
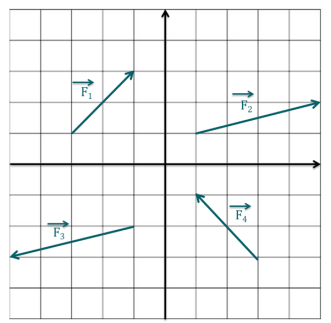
Correction
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Soit un objet ponctuel peut être soumis à plusieurs forces présentées dans le schéma ci dessous.
Parmi les propositions suivantes, quelle(s) combinaison(s) de forces tire le plus l'objet vers le haut ?

Correction
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Un objet ponctuel peut être soumis à plusieurs forces présentées dans le schéma ci-dessous.
Parmi les propositions suivantes, quelle(s) combinaison(s) de forces tire le plus l'objet vers la gauche ?

Correction
Explication Générale
Cf graphe.
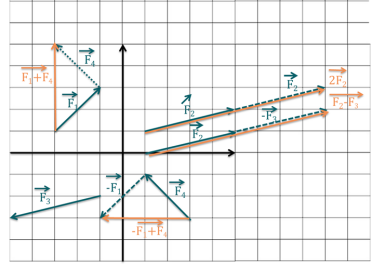
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Quelle(s) est (sont) la (les) affirmation(s) vraie(s) parmi les propositions suivantes ?
Correction
Explication Générale
Graphiquement :
Il faut voir les vecteurs comme des déplacements dans le plan. Additionner deux vecteurs c'est se déplacer du premier vecteur, puis du deuxième.
Pour additionner deux vecteurs on met le début du deuxième vecteur à la fin du premier vecteur. Le vecteur somme relie le point de départ et le point d'arrivée :
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Trois forces agissent en un point P comme représenté sur la figure. Ces trois forces sont dans un même plan et leur résultante est \(\overrightarrow{F}=\overrightarrow{T_1} + \overrightarrow{T_2} + \overrightarrow{T_3}\).
Quelle est la norme du vecteur force \(\overrightarrow{F}\) résultant ?
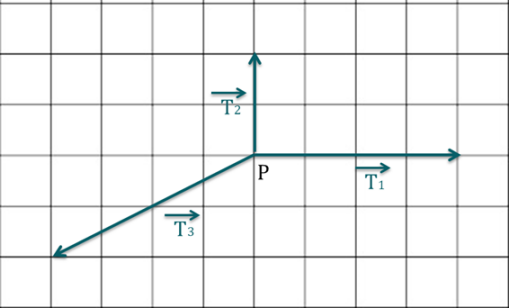
Correction
Explication Générale
Il faut faire la somme vectorielle graphiquement et on constate que le vecteur résultant est nul car \(\overrightarrow{T_1}+\overrightarrow{T_2} = - \overrightarrow{T_3}\).
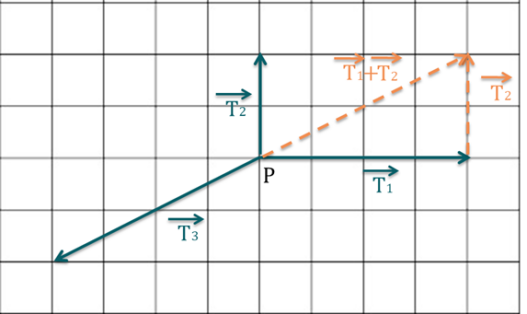
?Représenter une grandeur physique avec un vecteur
Énoncé
Calculatrice autorisée
Le champ de pesanteur terrestre est modélisé par un vecteur\( \vec{g}\) dont la direction est verticale, le sens vers les bas et la norme vaut environ 10 m/s²
Comment peut on écrire la coordonnée \(g_z\) de ce vecteur ?
Correction
Explication Générale
Les coordonnées du vecteur doivent tenir compte du repère choisi.
Un vecteur aura une coordonnée positive dans un repère orienté dans le même sens que le vecteur et une coordonnée négative dans un repère orienté dans l'autre sens.
?Représenter une grandeur physique avec un vecteur
Énoncé
Le point M est repéré dans le plan par ses coordonnées \((x,y)\). Le vecteur \(\overrightarrow{OM}\) a pour norme \(r\) et forme un angle \(\theta\) avec l'axe des abscisses.
\(r=5\) cm et \(\theta=40\)°
Que vaut \(x\) ?
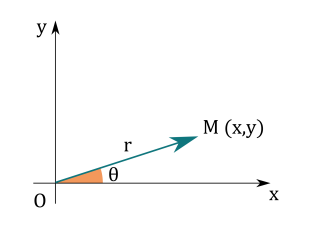
Correction
Explication Générale
\(x=r \cos(\theta)\)
Il faut faire l'application numérique en faisant attention à ce que la calculatrice soit bien en mode degrés et non radians.
\(x=5\times \cos(40°)=3,83\) cm
L'arrondi se fait à 1 ou 2 chiffres significatifs (40° : 2 chiffres significatifs, 5 cm : 1 chiffre significatif)
?Représenter une grandeur physique avec un vecteur
Énoncé
Le point M est repéré dans le plan par ses coordonnées \((x,y)\). Le vecteur \(\overrightarrow{OM}\) a pour norme \(r\) et forme un angle \(\theta\) avec l'axe des abscisses.
\(x=5\) cm et \(\theta=40\)°
Que vaut \(r\) ?

Correction
Explication Générale
\(r=\frac{x}{ \cos(\theta)}\)
Il faut faire l'application numérique en faisant attention à ce que la calculatrice soit bien en mode degrés et non radians.
\(x=\frac{5 }{\cos(40°)}=6,527\) cm
L'arrondi se fait à 1 ou 2 chiffres significatifs (40° : 2 chiffres significatifs, 5 cm : 1 chiffre significatif)
?Représenter une grandeur physique avec un vecteur
Énoncé
Le point M est repéré dans le plan par ses coordonnées \((x,y)\). Le vecteur \(\overrightarrow{OM}\) a pour norme \(r\) et forme un angle \(\theta\) avec l'axe des abscisses.
\(x=3\) cm et \(y=4\) cm
Que vaut \(r\) ?

Correction
Explication Générale
Le théorème de Pythagore appliqué dans le triangle rectangle dont l'hypoténuse est OM, et dont les deux autres côtés ont pour longueur x et y.
\(r^2=x^2+y^2 \rightarrow r=\sqrt{x^2+y^2}\)
Application numérique : \(r=\sqrt{3^2+4^2}=\sqrt{25}=5 cm\)
?Représenter une grandeur physique avec un vecteur
Énoncé
Le point M est repéré dans le plan par ses coordonnées \((x,y)\). Le vecteur \(\overrightarrow{OM}\) a pour norme \(r\) et forme un angle \(\theta\) avec l'axe des abscisses.
\(x=3\) cm et \(y=4\) cm
Que vaut \(\theta\) ?

Correction
Explication Générale
On rappelle que \(\tan(\theta)=\frac{oppose}{adjacent}=y/x\)
Dons \(\theta=\arctan(\frac{y}{x})\)
Application numérique : \(\theta=\arctan(\frac{4}{3})=0,93\) rad ou \(\theta=53,1°\)
?Représenter une grandeur physique avec un vecteur
Énoncé
Un pendule est soumis à la force de tension du fil \(\overrightarrow T\) et à son poids \(\overrightarrow P\). On veut décrire ces forces dans la base \(\left( \overrightarrow{e_r},\overrightarrow{e_\theta}\right)\).
Quelles sont les composantes de \(\overrightarrow T\) dans la base \(\left( \overrightarrow{e_r},\overrightarrow{e_\theta}\right)\) ?
Correction
Explication Générale
Le vecteur \(\overrightarrow{T}\) est un vecteur qui a la même direction que \(\overrightarrow{e_r}\) mais qui est de sens opposé et de norme \(T\). Il n'a pas de composante dans la direction de \(\overrightarrow{e_\theta}\).
Dans la notation en vecteur colonne, la première ligne correspond à la composante selon le premier vecteur de la base (ici \(\overrightarrow{e_r}\)).
On a donc : \(\overrightarrow{T}=\begin{pmatrix} -T\\0\end{pmatrix}\)
?Représenter une grandeur physique avec un vecteur
Énoncé
Un pendule est soumis à la force de tension du fil \(\overrightarrow T\) et à son poids \(\overrightarrow P\). On veut décrire ces forces dans la base \(\left( \overrightarrow{e_r},\overrightarrow{e_\theta}\right)\).

Quelle est la composante de \(\overrightarrow P\) selon \( \overrightarrow{e_r}\) ?
Correction
Explication Générale
1) On commence par dessiner le triangle rectangle dont l'hypoténuse est le vecteur \(\overrightarrow{P}\) et dont l'un des côtés est la projection de \(\overrightarrow{P}\) sur \(\overrightarrow{e_r}\).
2) On identifie ensuite le côté opposé : \(P\sin\theta\) et le côté adjacent :\(P\cos\theta\).
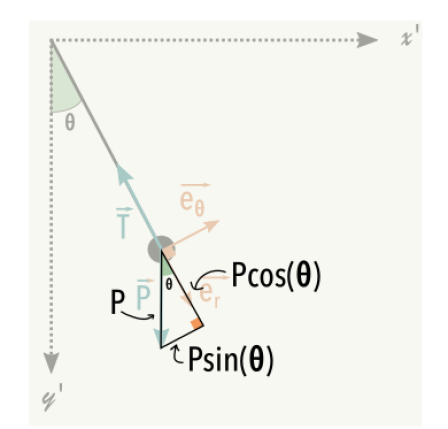
3) L'énoncé nous demande la composante selon \(\overrightarrow{e_r}\), donc la norme de cette composante est \(P\cos\theta\).
4) Le poids agit dans le même sens que \(\overrightarrow{e_r}\), il faut donc mettre un signe plus.
?Représenter une grandeur physique avec un vecteur
Énoncé
Un pendule est soumis à la force de tension du fil \(\overrightarrow T\) et à son poids \(\overrightarrow P\). On veut décrire ces forces dans la base \(\left( \overrightarrow{e_r},\overrightarrow{e_\theta}\right)\).

Quelle est la composante de \(\overrightarrow P\) selon \( \overrightarrow{e_\theta}\) ?
Correction
Explication Générale
1) On commence par dessiner le triangle rectangle dont l'hypoténuse est le vecteur \(\overrightarrow{P}\) et dont l'un des côtés est la projection de \(\overrightarrow{P}\) sur \(\overrightarrow{e_r}\)
(on a choisit le vecteur de la base le plus "pratique" mais il est tout à fait possible de travailler en projetant sur \(\overrightarrow{e_\theta}\))
2) On identifie ensuite le côté opposé : \(P\sin\theta\) et le côté adjacent : \(P\cos\theta\).

3) L'énoncé nous demande la composante selon \(\overrightarrow{e_\theta}\), donc la norme de cette composante est \(P\sin\theta\).
4) Le poids agit dans le sens opposé de \(\overrightarrow{e_r}\), il faut donc mettre un signe moins.
?Représenter une grandeur physique avec un vecteur
Énoncé
Dans un référentiel terrestre R supposé galiléen, on étudie le mouvement d'une bille roulant sans glisser sur un dôme hémisphérique (voir figure). La bille est en contact ponctuel avec le dôme au point A. On repère les composantes des vecteurs dans la base de vecteurs unitaires \(\left( \overrightarrow{e_\rho},\overrightarrow{e_\theta}\right)\).
Quelles sont les composantes du vecteur \(\overrightarrow{AC}\) dans la base \(\left( \overrightarrow{e_\rho},\overrightarrow{e_\theta}\right)\) ?
Correction
Explication Générale
Raisonnement : Pour aller de A à C, il faut se déplacer de la distance \(r\) selon \(\overrightarrow{e_\rho}\) et de 0 selon \(\overrightarrow{e_\theta}\).
Calcul : On a donc : \( \overrightarrow{AC}=r \overrightarrow{e_\rho}.\)
Pour exprimer le résultat en colonne on met donc les composantes de \(\overrightarrow{AC}\) dans un vecteur colonne : \(\overrightarrow{AC}=\begin{pmatrix} r\\0\end{pmatrix}\)
?Points cocycliques
Énoncé
Soient \(A, B, C\) et \(D\) quatre points 2 à 2 distincts et non alignés, \(M\) un point différent de ces points. \(A, B, C\) et D appartiennent au cercle de centre \(M\) si, et seulement si :
Correction
?Points cocycliques
Énoncé
4 points \(A, B, C\) et \(D\) d'affixes respectifs, \(a, b, c\) et \(d\), 2 à 2 distincts sont cocycliques ou alignés si, et seulement si,
Correction
?Linéarisation
Énoncé
Coche la ou les bonne(s) réponse(s)
Correction
Explication Générale
On utilise la formule de Moivre
?Linéarisation
Énoncé
Coche la ou les bonne(s) réponses
Correction
?Linéarisation
Énoncé
Coche la ou les bonne(s) réponse(s)
Correction
?Linéarisation
Énoncé
Coche la ou les bonne(s) réponse(s)
Correction
?Linéarisation
Énoncé
Coche la ou les bonne(s) réponse(s)
Correction
?Linéarisation
Énoncé
Coche la bonne réponse
Correction
?Linéarisation
Énoncé
Coche la bonne réponse
Correction
?Linéarisation
Énoncé
Coche la bonne réponse
Correction
?Linéarisation
Énoncé
Coche la bonne réponse
Correction
?Linéarisation
Énoncé
Coche la bonne réponse
Correction
?Forme exponentielle
Énoncé
Coche la ou les bonnes réponses
Correction
?Forme exponentielle
Énoncé
Soit le nombre complexe \(z_1=4e^{i\frac{\pi}{4}}\)
Correction
?Forme exponentielle
Énoncé
Soit le nombre complexe \(z_2=3ie^{i\frac{\pi}{6}}\)
Correction
?Forme exponentielle
Énoncé
Soit le nombre complexe \(z=-2e^{i\frac{2\pi}{3}}\)
Correction
?Forme exponentielle
Énoncé
Soit les nombres complexes \(z_1=4e^{i\frac{\pi}{4}}\) et \(z_2=3ie^{i\frac{\pi}{6}}\)
Correction
?Forme exponentielle
Énoncé
Soient les nombres complexes \(z_1=4e^{i\frac{\pi}{4}}\), \(z_2=3ie^{i\frac{\pi}{6}}\) et \(z_3=-2e^{i\frac{2\pi}{3}}\)
Correction
?Forme exponentielle
Énoncé
Soit le nombre complexe \(z_1=1+e^{ia}\), \(a \in [0 ;\pi]\)
Correction
?Forme exponentielle
Énoncé
Soit le nombre complexe \(z_2=1-e^{ia}\), \(a \in [0 ;\pi]\)
Correction
?Forme exponentielle
Énoncé
Soit le nombre complexe \(z=e^{ia}+e^{ib}\) \(a \in [0 ;\pi]\) et \(b \in [0 ;\pi]\)
Correction
?Forme exponentielle
Énoncé
Soit le ombre complexe \(z=\frac{1+e^{ia}}{1+e^{ib}}\) \(a \in [0 ;\pi]\) et \(b \in [0 ;\pi]\)
Correction
?Variables aléatoires
Énoncé
On considère un dé cubique truqué dont les faces sont numérotées de 1 à 6 et on note \(X\) la variable aléatoire donnée par le numéro de la face du dessus. On suppose que le dé est truqué de sorte que la probabilité d'obtenir une face est proportionnelle au numéro inscrit sur cette face.
\(P(X = 6)\) est égal à :
Correction
?Statistiques
Énoncé
On soumet un litre de sang à différentes valeurs de pression partielle en dioxygène\( (PO_2 )\), on mesure alors le volume de dioxygène fixé sur l'hémoglobine. Les résultats sont reproduits dans le tableau ci-dessous :
\(PO_2\) (en kPa) | 1,4 | 3 | 4,2 | 5,6 | 7,4 | 8,4 |
Volume d'\(O_2\) fixé sur l'hémoglobine (en mL par litre de sang) | 16 | 56 | 110 | 148 | 160 | 170 |
Correction
?Statistiques
Énoncé
On soumet un litre de sang à différentes valeurs de pression partielle en dioxygène \((PO_2 )\), on mesure alors le volume de dioxygène fixé sur l'hémoglobine. Les résultats sont reproduits dans le tableau ci-dessous :
\(PO_2\) (en kPa) | 1,4 | 3 | 4,2 | 5,6 | 7,4 | 8,4 |
Volume d\('O_2\) fixé sur l'hémoglobine (en mL par litre de sang) | 16 | 56 | 110 | 148 | 160 | 170 |
Correction
?Statistiques
Énoncé
On considère le tableau obtenu à partir du précédent en indiquant le rang de l'année et la consommation de pain correspondante :
Année | 1950 | 1960 | 1970 | 1980 | 1985 | 1990 | 1995 | 1996 |
Rang de l'année : \(x_i\) | 0 | 10 | 20 | 30 | 35 | 40 | 45 | 46 |
Consommation de pain en kg par an et par habitant \(:y_i\) | 121,7 | 100,0 | 80,3 | 70,6 | 66,3 | 63,4 | 59,6 | 60,0 |
Correction
?Statistiques
Énoncé
On considère le tableau obtenu à partir du précédent en indiquant le rang de l'année et la consommation de pain correspondante :
Année | 1950 | 1960 | 1970 | 1980 | 1985 | 1990 | 1995 | 1996 |
Rang de l'année : \(x_i\) | 0 | 10 | 20 | 30 | 35 | 40 | 45 | 46 |
Consommation de pain en kg par an et par habitant \(:y_i\) | 121,7 | 100,0 | 80,3 | 70,6 | 66,3 | 63,4 | 59,6 | 60,0 |
Correction
?Statistiques
Énoncé
6. On considère le tableau obtenu à partir du précédent en indiquant le rang de l'année et la consommation de pain correspondante :
Année | 1950 | 1960 | 1970 | 1980 | 1985 | 1990 | 1995 | 1996 |
Rang de l'année : \(x_i\) | 0 | 10 | 20 | 30 | 35 | 40 | 45 | 46 |
Consommation de pain en kg par an et par habitant \(:y_i\) | 121,7 | 100,0 | 80,3 | 70,6 | 66,3 | 63,4 | 59,6 | 60,0 |
Correction
?Encadrement d'une suite numérique
Énoncé
Pour tout entier naturel \(n\), on donne \( U_{n} = 2^n\) et \(V_n = n^2\) . Cocher la bonne réponse
Correction
?Encadrement d'une suite numérique
Énoncé
Pour tout entier naturel \(n\), on donne \(U_n = 3^n\) et \(V_n = n^3\) . Cocher la bonne réponse
Correction
?Encadrement d'une suite numérique
Énoncé
Soit la suite \((U_n)\) définie sur \(\mathbb{N}^*\) par :\( U_n =\frac{1}{1^2}+\frac{1}{2^2}+.....+\frac{1}{n^2}\) Pour tout entier naturel, on a :
Correction
?Suites numériques
Énoncé
Soit \(U_n\) la suite définie sur \(\mathbb{N}\) par : \(U_0=1\) et \(U_{n+1}=\sqrt{2+U_n}\)
Correction
?Suites numériques
Énoncé
Soit \(U_n\) la suite définie sur \(\mathbb{N}\) par : \(U_0=1\) et \(U_{n+1}=\frac{1}{2}U_n+1\)
Correction
?Suites numériques
Énoncé
Soit la suite \((U_n)\) définie sur \(\mathbb{N}\) par : \(U_0=\frac{1}{2}\) et \(U_{n+1}=\frac{e^{U_n}}{U_n+2}\)
Correction
?Suites numériques
Énoncé
Soit la suite U_n définie sur\( \mathbb{N}\) par : \(U{n+1}=U_n-U_n^2\)
Correction
?Suites numériques
Énoncé
Soit la suite \((U_n\) ) définie sur \(\mathbb{N}\) par : \(U_{n+1}=ln(1+U_n)\)
Correction
?Suites - Suites arithmétiques et suites géométriques
Énoncé
Soit \((u_n)\) la suite définie par : pour tout \(n\geqslant 1\), \(u_n=\dfrac 1{2^n}\). Cochez les bonnes réponses parmi les propositions suivantes.
Correction
Explication Générale
Il suffit d'appliquer la définition de la somme d'une suite géométrique de raison 1/2 et prendre en compte le fait que le premier terme est \(u_1=\dfrac 12\).
?Suites - Suites arithmétiques et suites géométriques
Énoncé
Soit \((u_n)\) la suite définie par : pour tout \(n\in\mathbf{N}\), \(u_n=\dfrac 1{2^n}\). Cochez les bonnes réponses parmi les propositions suivantes.
Correction
Explication Générale
Il suffit d'appliquer la définition de la somme d'une suite géométrique de raison 1/2 et prendre en compte le fait que le premier terme est \(u_0=1\).
?Suites - Suites arithmétiques et suites géométriques
Énoncé
On considère la somme \(S\) définie par \(\displaystyle\sum_{k=10}^{100} k=10+11+\cdots+100\). Cochez les bonnes réponses parmi les propositions suivantes.
Correction
Explication Générale
Il suffit d'appliquer la définition de la somme d'une suite arithmétique de raison 1 et prendre en compte le fait que le premier terme est \(10\).
?Suites - Suites arithmétiques et suites géométriques
Énoncé
On considère la somme \(S\) définie par \(\displaystyle\sum_{k=11}^{101} k=11+12+\cdots+101\). Cochez les bonnes réponses parmi les propositions suivantes.
Correction
Explication Générale
Il suffit d'appliquer la définition de la somme d'une suite arithmétique de raison 1 et prendre en compte le fait que le premier terme est \(11\).
?Suites - Suites arithmétiques et suites géométriques
Énoncé
On considère la somme \(S\) définie par \(\displaystyle\sum_{k=0}^{100} k\). Cochez les bonnes réponses parmi les propositions suivantes.
Correction
Explication Générale
Il suffit d'appliquer la définition de la somme d'une suite arithmétique de raison 1 et prendre en compte le fait que le premier terme est \(1\) car \(0\) est neutre.
?Suites - Suites arithmétiques et suites géométriques
Énoncé
On considère la somme \(S\) d'une suite arithmétique \((u_n)\): \(u_{10}+u_{11}+\cdots+u_{30}\). Cochez les bonnes réponses parmi les propositions suivantes.
Correction
Explication Générale
Il suffit d'appliquer la définition de la somme d'une suite arithmétique.
?Suites - Suites arithmétiques et suites géométriques
Énoncé
On considère la somme \(S\) d'une suite arithmétique \((u_n)\): \(u_{10}+u_{11}+\cdots+u_{30}\). Cochez les bonnes réponses parmi les propositions suivantes.
Correction
Explication Générale
Il suffit d'appliquer la définition de la somme d'une suite arithmétique.
?Suites - Suites arithmétiques et suites géométriques
Énoncé
On considère la somme \(S\) d'une suite géométrique \((u_n)\): \(u_{10}+u_{11}+\cdots+u_{30}\). Cochez les bonnes réponses parmi les propositions suivantes.
Correction
Explication Générale
Il suffit d'appliquer la définition de la somme d'une suite géométrique.
?Suites - Suites arithmétiques et suites géométriques
Énoncé
On considère la somme \(S\) d'une suite géométrique \((v_n)\): \(v_{10}+v_{11}+\cdots+v_{30}\). Cochez les bonnes réponses parmi les propositions suivantes.
Correction
Explication Générale
Il suffit d'appliquer la définition de la somme d'une suite géométrique.
?Suites - Suites arithmétiques et suites géométriques
Énoncé
Cochez les bonnes réponses parmi les propositions suivantes.
Correction
Questions d'analyse
?Question
Énoncé
En informatique, un nombre entier \(\textstyle{n}\) est codé par une suite \(\textstyle{l_i}\) de \(\textstyle{0}\) et de \(\textstyle{1}\) appelés bits de sorte que \(\textstyle{n=l_0+2l_1+2^2l_2+\cdots}\) . Par exemple, \(\textstyle{13}\) est codé par \(\textstyle{(1,0,1,1)}\) car \(\textstyle{13=1+0\times 2+2^2+2^3}\)
On appelle octet un regroupement de \(\textstyle{8}\) bits. En allumant un ordinateur, une case mémoire de la taille d'un octet est initialisée de telle sorte que chaque bit de cet octet prend la valeur \(\textstyle{1}\) avec probabilité \(\textstyle{p}\) , où \(\textstyle{0<p<1}\) , et ce, de façon indépendante des autres bits. On note \(\textstyle{X}\) la variable aléatoire donnant la valeur de l'entier dont cet octet est l'écriture en base \(\textstyle{2}\)
Correction
?Question
Énoncé
Tous les élèves d'une classe de \(\textstyle{35}\) étudient au moins une langue, allemand, anglais ou espagnol. \(\textstyle{11}\) parlent allemand, \(\textstyle{20}\) anglais et \(\textstyle{14}\) espagnol. Parmi eux, \(\textstyle{5}\) parlent anglais et espagnol, \(\textstyle{4}\) anglais et allemand et \(\textstyle{3}\) espagnol et allemand. On tire un élève au hasard dans la classe. Quelle est la probabilité qu'il parle les trois langues?
Correction
Explication Générale
Soit \(\textstyle{x}\) le nombre d'élèves apprenant les trois langues. On a \(\textstyle{5-x}\) élèves apprenant uniquement l'anglais et l'espagnol et \(\textstyle{4-x}\) apprenant uniquement l'anglais et l'allemand. Sur les \(\textstyle{20}\) élèves anglicistes, il reste \(\textstyle{20-\left((4-x)+(5-x)+x\right)}\) élèves n'apprenant que l'anglais, soit \(\textstyle{11+x}\) élèves. On fait de même pour les autres langues et l'on obtient le schéma ci-dessous. On a alors : \(\textstyle{(11+x)+(4+x)+(6+x)+(4-x)+(5-x)+(3-x)=35}\) soit \(\textstyle{x=2}\)

L'univers est l'ensemble des élèves, et il y a équiprobabilité, d'où la réponse \(\textstyle{\dfrac2{35}}\)
?Question
Énoncé
Une urne contient \(\textstyle{5}\) cartons portant les numéros, \(\textstyle{1}\) , \(\textstyle{2}\) , \(\textstyle{3}\) , \(\textstyle{4}\) et \(\textstyle{5}\) . On tire au hasard, successivement et sans remise \(\textstyle{3}\) cartons. Quelle est la probabilité d'avoir au moins un numéro pair ?
Correction
Explication Générale
On peut représenter les tirages par un arbre, comme celui ci-dessous où quelques résultats ont été notés. Il y a \(\textstyle{5\times4\times3=60}\) résultats possibles. Il y a équiprobabilité. On demande la probabilité de l'événement contraire de l'événement \(\textstyle{A}\) : « tous les numéros sont impairs». Il y a \(\textstyle{3\times2\times1}\) résultats qui réalisent \(\textstyle{A}\) , donc \(\textstyle{\mathbb P(A)=\dfrac6{60}=\dfrac1{10}}\)
La probabilité cherchée est donc \(\textstyle{1-\dfrac1{10}=\dfrac9{10}}\)

?Question
Énoncé
Le domaine de définition de la fonction \(f\) de la variable réelle définie par \(f:x\mapsto\ln(\sqrt{x}-\sqrt{2-x})\) est
Correction
Explication Générale
On note \(D\) le domaine de définition.
La fonction racine étant définie sur \(\mathbb R_+\) il faut \(x \geq 0\) et \(2-x \geq 0\), c'est-à-dire \(x \geq 0\) et \(x \leq 2\), d'où \(D\) inclus dans \([0,2]\)
\(\ln\) est définie sur \(\mathbb R_+^*\) il faut \(\sqrt(x)-\sqrt(2-x)>0\), ce qui équivaut à \(x>2-x\) (car \(x\) et \(2-x\) sont positifs), soit \(x>1\). Ainsi \(D\subset]1,2]\). On a bien pour tout \(x\in]1,2]\) que \(f(x)\) est bien défini : \(D=]1,2]\).
?Question
Énoncé
Grâce à la l'étude de la fonction \(f:x \mapsto \frac{\ln(x)}{x}\), on peut affirmer que l'équation \(3\ln(x)=x \)
Correction
Explication Générale
On constate que \(3\ln(x)=x\) si et seulement si \(f(x)=\frac{1}{3}\). \(f'(x)=\frac{1-\ln(x)}{x^2}\) donc est positive sur \(]0,\rm e]\), s'annule en \(\rm e\) et est négative sur \([\rm e, +\infty[\). \(f\) est donc croissante sur \(]0,\rm e]\), décroissante sur \([\rm e, +\infty[\). Comme \(\lim\limits_{x\to 0^+}f(x)=-\infty\), \(f(\rm e)={\rm e}^{-1}>\frac{1}{3}\) et \(\lim\limits_{x\to +\infty}f(x)=0\), \(f(x)=\frac{1}{3}\) admet deux solutions : une entre \(0\) et \(\rm e\), l'autre entre \(\rm e\) et \(+\infty\).
Voici deux ressources pour revoir quelques notions :
?Question
Énoncé
On admet qu'il existe trois réels \(a\), \(b\) et \(c\) tels que pour tout \(x\) différent de \(1\) et de \(-3\), on ait l'égalité \(\frac{x}{(x-1)(x+3)^2}=\frac{a}{x-1}+\frac{b}{x+3}+\frac{c}{(x+3)^2}.\) On en déduit que
Correction
Explication Générale
On réduit au même dénominateur : \(\frac{a}{x-1}+\frac{b}{x+3}+\frac{c}{(x+3)^2}=\frac{a(x+3)^2+b(x-1)(x+3)+c(x-1)}{(x-1)(x+3)^2}\). On a donc l'égalité \(\frac{a(x+3)^2+b(x-1)(x+3)+c(x-1)}{(x-1)(x+3)^2}=\frac{x}{(x-1)(x+3)^2}\), et, en multipliant par \((x-1)(x+3)^2\), \(a(x+3)^2+b(x-1)(x+3)+c(x-1)=x\). On développe :
\(ax^2+6ax+9a+bx^2+2bx-3b+cx-c=x\)
\((a+b)x^2+(6a+2b+c)x+9a-3b-c=x\) : la réponse 1) est juste
\((a+b)x^2+(6a+2b+c-1)x+9a-3b-c=0\) pour tout \(x\) différent de \(1\) et \(-3\) : ce polynôme admet une infinité de racines, donc c'est le polynôme nul, c'est-à-dire
\(a+b=0\), \(6a+2b+c-1=0\), \(9a-3b-c=0\). La résolution de ce petit système donne \(a=\frac{1}{16},\,b=-\frac{1}{16},\,c=\frac{3}{4}\).
?Question
Énoncé
L'équation \({\rm e}^{2x}- 7{\rm e}^{x}+1=0\)
Correction
?Question
Énoncé
Soit\( (v_n)_{n\ge 0}\) une suite réelle géométrique de raison \(\frac{2}{3}\). On définit la suite\( (w_n)_{n\ge 0}\) en posant \(w_0= v_0\) et \(w_{n+1}= w_n+v_{n+1}\) pour \(n\ge 0 \)
Correction
Explication Générale
On peut commencer par calculer les premiers termes de \((w_n)\) (on pose \(a=\frac{2}{3}\)) : \(w_0=v_0\), \(w_1=v_0+a v_0=v_0(1+a)\), \(w_2=v_0(1+a+a^2)\), \(w_3=v_0(1+a+a^2+a^3)\). En se souvenant que \(1+a+a^2+\dots+a^m=\frac{1-a^{m+1}}{1-a}\) (\(a\neq 1\)), on a \(w_2=v_0\frac{1-a^{3}}{1-a}\), \(w_3=v_0\frac{1-a^{4}}{1-a}\), et on peut supposer que \(w_n=v_0 \frac{1-a^{n+1}}{1-a}\). Cela se prouve par récurrence : on a fait l'initialisation, pour l'hérédité, supposons la propriété vraie au rang \(n\), montrons la au rang \(n+1\). \(w_{n+1}=w_n+v_{n+1}=v_0 \frac{1-a^{n+1}}{1-a}+v_0 a^{n+1}=v_0 \frac{1-a^{n+1}+a^{n+1}-a^{n+2}}{1-a}=v_0 \frac{1-a^{n+2}}{1-a}\), ce qu'il fallait démontrer. A partir de là, on voit que \((w_n)\) n'est ni géométrique, ni arithmétique, par contre elle converge vers \(v_0 \frac{1-0}{1-2/3}=3v_0\).
?Question
Énoncé
Quelle que soit la suite réelle arithmétique \((u_n)_{n\ge 0}\), on a
Correction
Explication Générale
Soit \((u_n)\) une suite arithmétique de raison \(a\). On a \(u_n=u_0+na\). En particulier, \(u_1+u_2+u_3=u_0+a+u_0+2a+u_0+3a=2u_0+u_0+6a=2u_0+u_6\). Les réponses 2 et 3 sont fausses, prendre par exemple la suite \(u_n=n+1\) pour s'en convaincre (\(10\neq 3\) et \(9\neq7\)). La réponse 4 est vraie : \(u_1+u_3=2u_0+4a=2u_2\).
?Question
Énoncé
La suite récurrente définie pour tout entier naturel \(n\) par : \(u_{n+1}=0.5u_n+1\) et \(u_0=0\) est :
Correction
Explication Générale
La suite \((u_n)\) vérifie la relation de récurrence \(u_{n+1}=f(u_n)\), où \(f :x\mapsto 0.5 x+1\). On a \(u_0=0\) et \(u_1=1\), donc \(u_0\leq u_1\), comme \(f\) est croissante, \(f(u_0)\leq f(u_1)\), c'est-à-dire \(u_1\leq u_2\), toujours par croissance de \(f\), \(f(u_1)\leq f(u_2)\), c'est-à-dire \(u_2\leq u_3\), et ainsi de suite : on montre par récurrence que \((u_n)\) est croissante. On montre aussi par récurrence que \(u_n\leq 2\). Initialisation : \(u_0=0\leq 2\). Hérédité : supposons \(u_n\leq 2\). \(u_{n+1}=0.5 u_n+1\leq 2\), ce qui achève la récurrence. La suite \((u_n)\) étant croissante majorée, elle converge. Comme pour \(n\geq 1\) \(u_n\geq u_1\), sa limite est supérieure à \(u_1\), donc différente de 1.
?Question
Énoncé
Pour tout nombre complexe non nul \(z\), notons par \(\overline z\) le conjugué de \(z\)
En général, le nombre complexe \(z^3-\overline z^3\) est :
Correction
?Question
Énoncé
On donne la courbe représentative d'une fonction \(f\) définie par \(f(x)=(\sin x)(2\cos x-1)\).
Correction
Explication Générale
\(f(x)=(\sin x)(2\cos x-1)=-\frac14\times2(2\sin x)(2\cos x-1)\) : \(f\) est égale à\(-\frac14\times2u'u\) avec \(u(x)=2\cos x-1\)
Une primitive \(F\) est donc égale à \(-\frac14u^2\), soit \(F(x)=-\frac14(2\cos x-1)2\).
Remarque : \((-\cos x)(2\sin x-x)\) n'est pas une primitive car une primitive d'un produit n'est pas le produit des primitives
\(\displaystyle\int_0^{3\pi/2}f(x)dx=\left[F(x)\right]_0^{3\pi/2}=\left[-\frac14(2\cos x-1)^2\right]_0^{3\pi/2}=-\frac14(0-1)^2+\frac14(2-1)^2=-\frac14+\frac14=0\)
Attention, il ne faut pas confondre intégrale et aire : le nombre\(\int_0^{3\pi/2}f(x)dx\) n'est pas égal à l'aire « sous la courbe » de \(f\) car \(f\) change de signe sur \(\left[0 ; \frac{3\pi}{2}\right]\)
La fonction \(f\) étant positive sur \(\left[0 ; \frac{\pi}{3}\right]\), négative sur \(\left[\frac{\pi}{3} ; \pi\right]\) et positive sur \(\left[\pi ; \frac{3\pi}{2}\right]\), on utilise la relation de Chasles pour calculer l'aire coloriée (notée \(A\) ). On obtient :
\(A=\int_{0}^{\pi/3}f(x)dx+\int_{\pi/3}^{\pi}-f(x)dx+\int_{\pi}^{3\pi/2}f(x)dx\)
\(=\left[-\frac14(2\cos x-1)^2\right]_{0}{\pi/3}+\left[\frac14(2\cos x-1)^2\right]_{\pi/3}^{\pi}+\left[-\frac14(2\cos x-1)^2\right]_{\pi}^{3\pi/2}\)
\(=-\frac14(1-1)^2+\frac14(2-1)^2+\frac14(-2-1)^2-\frac14(1-1)^2-\frac14(0-1)^2+\frac14(-2-1)^2\)
\(=\frac14+\frac94-\frac14+\frac94=\frac{18}{4}=\frac92\) soit \(4,5 u.a.\)
?Question
Énoncé
Soit \(f\) et \(g\) deux fonctions définies sur \(\mathbb R\), et soit \(a<b\). On suppose que \(\int_a^bf(t)dt\leq\int_a^bg(t)dt\). Alors
Correction
Explication Générale
L'affirmation "pour tout \(x \in [a ;b]\), on a \(f(x)\leq g(x)\)" est fausse : prenons un exemple pour s'en convaincre, posons \(g(x)=x\), \(f(x)=\frac13\), \(a=0\) et \(b=1\). On a bien \(\displaystyle{\int_0^1f(t)dt = \frac13 \leq \int_0^1g(t)dt = \bigg[\frac{t^2}{2}\bigg]^1_0 = \frac12}\) MAIS on n'a pas \(f(x)\leq g(x)\) pour tout \(x \in [0 ;1]\), puisque pour tout \(x \in \bigg[0 ;\frac13\bigg[\) on a \(g(x) <f(x)\). La "croissance de l'intégrale" n'est donc qu'une implication, sa réciproque est fausse comme le montre cet exemple.
Les affirmations "pour tout \(x\in [a ;b]\), on a \(\int_a^xf(t)dt\leq \int_a^xg(t)dt\)" et "si \(f\) et \(g\) sont positives sur \([a ;b]\), alors on a \(\int_a^x f(t)dt\leq\int_a^xg(t)dt\) pour tout \(x\in [a ;b]\)" sont fausses également. En reprenant les mêmes exemples que précédemment, puisque \(f\) et \(g\) sont positives sur \([0 ;1]\), on a \(G(x) = \int_a^xg(t)dt =\bigg[\frac{t^2}{2}\bigg]^x_0 = \frac{x^2}{2}\) (la fonction \(G(x) = \int_a^xg(t)dt\) est, d'après le théorème fondamental de l'intégration, la primitive de \(g\) qui s'annule en \(a\)), et on a \(F(x)=\int_a^xf(t)dt=\bigg[\frac{t}{3}\bigg]^x_0=\frac{x}{3}\). Pour \(x=\frac12\), on a \(F\bigg(\frac12\bigg) = \frac16 > G\bigg(\frac12\bigg) = \frac18\), ce qui montre que la relation \(\int_a^xf(t)dt \leq \int_a^xg(t)dt\) n'est pas vérifiée pour tout \(x\in[a ;b]\).
L'affirmation "l'intégrale \(\int_a^b(g(t)-f(t))dt\) est positive" est juste : par linéarité de l'intégrale, on a \(\int_a^b(g(t)-f(t))dt = \int_a^bg(t)dt - \int_a^bf(t)dt \geq 0\) par hypothèse de l'énoncé.
?Question
Énoncé
Soit \(a>0\), \(a\neq1\).
Correction
Explication Générale
Les bonnes réponses sont \(\lim\limits_{a \rightarrow + \infty} \displaystyle\int_a^{a^2}xe^{-x^2}dx=0\) et \(\lim\limits_{x \rightarrow + \infty}\displaystyle \int_a^{a^2}xe^{-x^2}dt=0\).
L'affirmation "On a \(\lim\limits_{x \rightarrow + \infty}\displaystyle \int_a^{a^2}xe^{-x^2}dx=0\)" est fausse (et n'a pas grand sens) : en effet, l'intégrale \(\displaystyle \int_a^{a^2}xe^{-x^2}dx\) ne dépend pas de la variable muette \(x\), donc à \(a\) fixé cette quantité est constante et non nulle (puisque \(a^2\neq a\) car \(a\neq 0\) et \(a \neq 1\), et que la fonction \(x\mapsto xe^{-x^2}\) est strictement positive sur \(\mathbb{R}\)).
L'affirmation "On a \(\lim\limits_{a \rightarrow + \infty} \displaystyle\int_a^{a^2}xe^{-x^2}dx=0\)" est juste : notons \(f(x)=xe^{-x^2}.\) On constate que \(f(x)=-\frac12u'(x)e^{u(x)},\) où \(u(x)=-x^2.\) On peut donc choisir comme primitive de \(f\) la fonction \(F(x)=-\frac12e^{u(x)}=-\frac12e^{-x^2}\). On a alors, par le théorème fondamentale de l'intégration, l'égalité \(\displaystyle \int_a^{a^2}xe^{-x^2}dx=F(a^2)-F(a)=-\frac12(e^{-a^{4}}-e^{-a^2}).\) Comme \(\lim\limits_{a \rightarrow + \infty} e^{-a^{4}}=\lim\limits_{a \rightarrow + \infty} e^{-a^2}=0\), on a bien \(\lim\limits_{a \rightarrow + \infty} \displaystyle\int_a^{a^2}xe^{-x^2}dx=0\).
L'affirmation "On a \(\lim\limits_{x \rightarrow + \infty}\displaystyle \int_a^{a^2}xe^{-x^2}dt=0\)" est juste : ici l'intégrale \(\displaystyle \int_a^{a^2}xe^{-x^2}dt\) est facile à calculer, car la fonction \(t\mapsto xe^{-x^2}\) ne dépend pas de la variable d'intégration \(t\). Cette intégrale vaut donc \(xe^{-x^2}(a^{2}-a)\). Comme, par croissance comparée, on a \(\lim\limits_{x\rightarrow+\infty}xe^{-x^2}=0\), on en déduit que \(\lim\limits_{x\rightarrow+\infty}xe^{-x^2}(a^2-a)=0\), et donc que \(\lim\limits_{x \rightarrow + \infty}\displaystyle \int_a^{a^2}xe^{-x^2}dt=0\).
L'affirmation "On a \(\lim\limits_{a \rightarrow + \infty} \displaystyle\int_a^{a^2}xe^{-x^2}dt=+\infty\)" n'est pas juste en général (cela dépend du signe de \(x\), qui n'est pas précisé ici). En effet, comme on l'a vu précédemment, on a \(\displaystyle \int_{a}^{a^{2}}xe^{-x^2}dt=xe^{-x^2}(a^2-a).\) On a \(\lim\limits_{a\rightarrow+\infty}a^2-a=\lim\limits_{a\rightarrow+\infty}a(a-1)=+\infty.\) Ainsi, si \(x>0\), on obtient \(\lim \limits_{a\rightarrow+\infty}xe^{-x^2}(a^2-a)=+\infty\), et si \(x<0\) on obtient \(\lim \limits_{a\rightarrow+\infty}xe^{-x^2}(a^2-a)=-\infty\).
?Question
Énoncé
Soit \(a>1\) un réel.
Correction
Explication Générale
Les bonnes réponses sont : \(\lim\limits_{a \rightarrow + \infty} \int_x^{x^2}\frac{\ln(a)}{a}dt=0\) et \(\lim\limits_{a \rightarrow + \infty} \int_a^{a^2}\frac{\ln(x)}{x}dx=+\infty\).
L'affirmation "On a \(\lim\limits_{x \rightarrow + \infty} \int_x^{x^2}\frac{\ln(a)}{a}dt=0\)" est fausse : en effet \(\lim\limits_{x \rightarrow + \infty} \int_x^{x^2}\frac{\ln(a)}{a}dt=(x²-x)\frac{\ln(a)}a\) (puisque la fonction que l'on intègre est constante par rapport à la variable \(t\)). Comme \(a>1\), la constante \(\frac{\ln(a)}a\) est strictement positive, et puisque \(\lim\limits_{x \rightarrow +\infty}x^2-x=\lim\limits_{x\rightarrow +\infty}x(x-1)=+\infty\), on en déduit que \(\lim\limits_{x \rightarrow + \infty}\displaystyle\int_x^{x^2}\frac{\ln(a)}adt=+\infty\).
L'affirmation "On a \(\lim\limits_{a \rightarrow + \infty} \int_x^{x^2}\frac{\ln(a)}{a}dt=0\)" est juste : comme ci-dessus, on a\(\displaystyle\int_x^{x^2}\frac{\ln(a)}adt=(x^2-x)\frac{\ln(a)}a.\) Par croissance comparée, on sait que \(\lim\limits_{a\rightarrow +\infty}\frac{\ln(a)}a=0\), donc à \(x\) fixé on a bien \(\lim\limits_{a\rightarrow +\infty}(x^2-x)\frac{\ln(a)}a=0\).
L'affirmation "On a \(\lim\limits_{x \rightarrow + \infty} \int_a^{a^2}\frac{\ln(x)}{x}dx=+\infty\)" est fausse, elle n'a d'ailleurs pas grand sens : en effet, la quantité \(\displaystyle\int_a^{a^2}\frac{\ln(x)}xdx\) est indépendante de la variable \(x\). Pour \(a\) fixé, la quantité \(I(a)=\displaystyle\int_a^{a^2}\frac{\ln(x)}xdx,\) est un nombre réel, qui ne dépend pas de \(x\), donc sa limite lorsque \(x\) tend vers \(+\infty\) est \(I(a)\).
L'affirmation "On a \(\lim\limits_{a \rightarrow + \infty} \int_a^{a^2}\frac{\ln(x)}{x}dx=+\infty\)" est juste : pour s'en convaincre, on va calculer à \(a\) fixé la valeur de \(I(a)=\displaystyle\int_a^{a^2}\frac{\ln(x)}xdx\). Par le théorème fondamental de l'intégrale, on sait que si \(G\) est une primitive de la fonction \(g(x)=\frac{\ln(x)}x,\) on a \(I(a)=G(a^2)-G(a)\). Or, comme la dérivée de la fonction \(u(x)=\ln(x)\) est \(u'(x)=\frac1x\), on constate que \(g(x)=u'(x)u(x)\) est la dérivée de la fonction \(x\mapsto\frac12[u(x)]^2\), donc \(G(x)=\frac12[\ln(x)]²\) est une primitive de \(g\). On en déduit que \(I(a)=\frac12[(\ln(a^2))^2-(\ln(a))^2]=\frac12[(2\ln(a))^2-(\ln(a))^2]=\frac32(\ln(a))^2\). On a alors \(\lim\limits_{a\rightarrow +\infty}I(a)=\lim\limits_{a\rightarrow +\infty}\frac32(\ln(a))^2=+\infty\).
?Les maïs nains
Énoncé
Les maïs nains sont homozygotes pour un gène récessif a qui représente 22 % des allèles à ce locus dans une population échantillonnée. Si on croise deux grands individus pris au hasard dans cette population, est-il possible d'obtenir des individus nains et avec quelle probabilité ?
Choisissez l'intervalle dans lequel se situe la probabilité d'avoir des descendants nains ?
Correction
Explication Générale
L'énoncé indique que la fréquence de l'allèle a = f(a) = q = 0,22
[grand] | [nain] |
AA + Aa | aa |
p² + 2pq | q² |
Les individus grands peuvent être de deux génotypes AA ou Aa. On pourrait envisager toutes les possibilités de couples entre grands. Cependant, pour que deux parents grands donnent un individu nain aa, il faut forcément que chacun des deux parents transmettent un allèle a. Donc la seule possibilité pour que deux parents grands donnent un descendant nain est que les deux parents soient hétérozygotes sachant qu'ils sont de phénotype [grand]. On parle ici de probabilité conditionnelle. La condition, qui nous est imposée dans l'énoncé est que les parents sont de phénotype [grand].
La probabilité d'être de phénotype [grand] est la probabilité d'être AA ou Aa soit f[grand] = f(AA) + f(Aa).
La probabilité d'être hétérozygote sachant qu'on est de phénotype [grand] est = f(Aa) / f[grand].
Ici, pour effectuer l'application numérique, il est nécessaire de poser que la population de maïs est à l'équilibre de Hardy-Weinberg pour le gène étudié. Ainsi, il est possible d'utiliser la relation entre fréquences alléliques et génotypiques pour calculer nos probabilités.
On considérera que la taille de l’échantillon est suffisamment grande pour considérer que la probabilité d'un événement est égal à sa fréquence.
p = 1 - 0,22 = 0,78 donc p² = 0,61 et 2pq = 0,34
f(Aa) / f[grand] = f(Aa) /( f(Aa) + f(AA)) = 0,34 / (0,34+0,61) = 0,36
Si on décompose la probabilité recherchée, probabilité d'avoir des descendants nains en croisant deux individus grands pris au hasard dans la population =P= probabilité que le père soit hétérozygote sachant qu'il est grand et probabilité que la mère soit hétérozygote sachant qu'elle est grande et probabilité que le père transmette son allèle a et probabilité que la mère transmette son allèle a.
Au final P = 0,36 x 0,36 x 1/2 x 1/2 = 0,032.
En moyenne, 3,2% des descendants de couples grands seront nains.
?Diagnostic prénatal 1
Énoncé
La mucoviscidose est une maladie génétique due à un allèle muté du gène CFFR. Cet allèle est à l'origine d'une diminution du transport des ions chlorure à travers la membrane des cellules des muqueuses. Le mucus sécrété par ces cellules, déshydraté et visqueux, obture alors les voies aériennes et digestives.
En Europe, un enfant est atteint sur 2 500 naissances.
Quelle est la probabilité pour l'individu IV1 à naître d'être malade ?
Correction
Explication Générale
D'après la généalogie, le gène de la maladie est récessif car deux parents sains peuvent avoir un enfant malade. Le gène est autosomal car une mère malade donne des garçons sains (si le gène était porté par X, tous les garçons seraient malades). Notons l'allèle malade a et sa fréquence q. L'allèle A a pour fréquence p.
La mère III8 a un frère malade. Puisque les parents sont de phénotypes sains, cela indique que les parents sont forcément hétérozygotes (chacun a transmis un allèle a mais aucun des deux n'est malade).
Pour que IV2 soit malade, il faut donc que sa mère lui transmette un allèle a. Puisque III8 est de phénotype sain, nous recherchons donc sa probabilité d'être hétérozygote sachant qu'elle est de phénotype sain.
Les deux parents de III8 sont hétérozygotes d'où le tableau de croisement suivant
gamètes II3 \ gamètes II4 | A de fréquence 1/2 | a de fréquence 1/2 |
A de fréquence 1/2 | AA en fréquence 1/4 | Aa en fréquence 1/4 |
a de fréquence 1/2 | Aa en fréquence 1/4 | aa en fréquence 1/4 |
On sait que III8 est de phénotype sain, cela exclut donc dans le tableau la possibilité d'être aa, d'ou le tableau suivant
gamètes II3 \ gamètes II4 | A de fréquence 1/2 | a de fréquence 1/2 |
A de fréquence 1/2 | AA en fréquence 1/3 | Aa en fréquence 1/3 |
a de fréquence 1/2 | Aa en fréquence 1/3 |
Ainsi, la probabilité de III8 d'être hétérozygote sachant qu'elle est de phénotype sain et 2/3.
D'autre part, le père est sain, il porte donc au moins un allèle A. Pour que IV1 soit malade, il faut que le père soit hétérozygote et lui transmette son allèle a.
La probabilité que le père soit hétérozygote sachant qu'il est de phénotype sain n'est pas juste la probabilité qu'il soit hétérozygote car il faut tenir compte du fait que l'individu est avec certitude de phénotype sain (comme précédemment). Cette probabilité conditionnelle est égale à la fréquence d'être hétérozygote sur la fréquence d'être de phénotype sain = f(Aa) /[ f(Aa) + f(AA)]=2pq / (2pq + p²)
Un enfant est atteint sur 2500 naissances signifie que f(aa) = 1/2500 = 0,0004 = q² donc f(a) = racine(1/2500) = 0,02
probabilité que le père soit hétérozygote sachant qu'il est de phénotype sain = 2 x 0,02 x 0,98 / ( 2 x 0,02 x 0,98 + 0,98²) = 0,392
La probabilité que l'enfant soit malade est donc la probabilité que le père soit hétérozygote sachant qu'il est de phénotype sain x la probabilité de transmettre l'allèle a x la probabilité pour la mère soit hétérozygote sachant qu'elle est de phénotype sain x la probabilité pour la mère de transmettre son allèle a sachant qu'elle est hétérozygote = 0,392 x 1/2 x 2/3 x 1/2 =0,065
?Diagnostic prénatal 2
Énoncé
La mucoviscidose est une maladie génétique due à un allèle muté du gène CFFR. Cet allèle est à l'origine d'une diminution du transport des ions chlorure à travers la membrane des cellules des muqueuses. Le mucus sécrété par ces cellules, déshydraté et visqueux, obture alors les voies aériennes et digestives.
En Europe, un enfant est atteint sur 2 500 naissances.

Quelle est la probabilité pour l'individu IV2 à naître d'être malade ?
Correction
Explication Générale
D'après la généalogie, le gène de la maladie est récessif car deux parents sains peuvent avoir un enfant malade. Le gène est autosomal car une mère malade donne des garçons sains (si le gène était porté par X, tous les garçons seraient malades). Notons l'allèle malade a et sa fréquence q. L'allèle A a pour fréquence p.
La mère de IV2, III10, ne peut être qu'hétérozygote car sa propre mère II5 est atteinte par la maladie. II5 est donc de génotype aa et a transmis un allèle a à III10. Cependant, III10est de phénotype sain donc de génotype Aa.
Pour que IV2 soit malade, il faut donc que sa mère lui transmette son allèle a avec la probabilité 1/2.
D'autre part, le père est sain, il porte donc au moins un allèle A. Pour que IV2 soit malade, il faut que le père soit hétérozygote et lui transmette son allèle a.
La probabilité que le père soit hétérozygote sachant qu'il est de phénotype sain n'est pas juste la probabilité qu'il soit hétérozygote car il faut tenir compte du fait que l'individu est avec certitude de phénotype sain. Cette probabilité conditionnelle est égale à la fréquence d'être hétérozygote sur la fréquence d'être de phénotype sain = f(Aa) /[ f(Aa) + f(AA)]=2pq / (2pq + p²)
Un enfant est atteint sur 2500 naissances signifie que f(aa) = 1/2500 = 0,0004 = q² donc f(a) = racine(1/2500) = 0,02
probabilité que le père soit hétérozygote sachant qu'il est de phénotype sain = 2 x 0,02 x 0,98 / ( 2 x 0,02 x 0,98 + 0,98²) = 0,392
La probabilité que l'enfant soit malade est donc la probabilité que le père soit hétérozygote sachant qu'il est de phénotype sain x la probabilité de transmettre l'allèle a x la probabilité pour la mère de transmettre son allèle a sachant qu'elle est hétérozygote = 0,392 x 1/2 x 1/2 =0,098
?Diagnostic prénatal 3
Énoncé
La mucoviscidose est une maladie génétique due à un allèle muté du gène CFFR. Cet allèle est à l'origine d'une diminution du transport des ions chlorure à travers la membrane des cellules des muqueuses. Le mucus sécrété par ces cellules, déshydraté et visqueux, obture alors les voies aériennes et digestives.
En Europe, un enfant est atteint sur 2 500 naissances.

Quel est le risque pour le couple II
1 et II
2 (couple génération II complètement à gauche) d'avoir un garçon atteint par la maladie ?
Correction
Explication Générale
D'après la généalogie, le gène de la maladie est récessif car deux parents sains peuvent avoir un enfant malade. Le gène est autosomal car une mère malade donne des garçons sains (si le gène était porté par X, tous les garçons seraient malades). Notons l'allèle malade a et sa fréquence q. L'allèle A a pour fréquence p.
La généalogie nous indique que II1 et II2 sont de phénotypes sains. II1 a une mère malade qui est de génotype aa et qui lui a transmis un allèle a. II1 est donc forcément hétérozygote Aa.
Pour que les descendants de II1 et II2 soit malades, il faut donc que la mère II1 transmette son allèle a avec la probabilité 1/2 et que le père soit hétérozygote sachant qu'il est de phénotype sain et transmette son allèle a avec la probabilité 1/2.
La probabilité que le père soit hétérozygote sachant qu'il est de phénotype sain n'est pas juste la probabilité qu'il soit hétérozygote car il faut tenir compte du fait que l'individu est avec certitude de phénotype sain (on exclut la possibilité d'être aa). Cette probabilité conditionnelle est égale à la fréquence d'être hétérozygote sur la fréquence d'être de phénotype sain = f(Aa) /[ f(Aa) + f(AA)]=2pq / (2pq + p²)
Un enfant est atteint sur 2500 naissances signifie que f(aa) = 1/2500 = 0,0004 = q² donc f(a) = racine(1/2500) = 0,02
probabilité que le père soit hétérozygote sachant qu'il est de phénotype sain = 2 x 0,02 x 0,98 / ( 2 x 0,02 x 0,98 + 0,98²) = 0,392
La probabilité que l'enfant soit malade est donc la probabilité que le père soit hétérozygote sachant qu'il est de phénotype sain x la probabilité de transmettre l'allèle a x la probabilité pour la mère de transmettre son allèle a sachant qu'elle est hétérozygote = 0,392 x 1/2 x 1/2 =0,098
?Matrices
Énoncé
Soit \(a,b\in \mathbb{R}\), \(A=\left(\begin{array}{rcc}a&1&b\\0&a&2\\ 0&0&a\\ \end{array}\right)\) et \(N= A-aI\), où \(I= \left(\begin{array}{rcc}1&0&0\\0&1&0\\ 0&0&1\\ \end{array}\right)\). Quelles sont les assertions vraies ?
Correction
Explication Générale
On a : \(N=\left(\begin{array}{rcc}0&1&b\\0&0&2\\ 0&0&0\\ \end{array}\right)\), \(N^2=\left(\begin{array}{rcc}0&0&2\\0&0&0\\ 0&0&0\\ \end{array}\right)\) et \(N^k=0, \) pour tout \(k\ge 3\).
On a : \(A= N+aI\). Comme le produit des matrices \(N\) et \(aI\) est commutatif, on peut appliquer la formule du binôme pour le calcul des puissances de \(A\).
?Matrices
Énoncé
Soit \(A= \left(\begin{array}{rcc}1&2&3\\0&1&2\\ 0&0&1\\ \end{array}\right)\) et \(N= A-I\), où \(I= \left(\begin{array}{rcc}1&0&0\\0&1&0\\ 0&0&1\\ \end{array}\right)\). On considère \(3\) suites récurrentes \((u_n)_{n\ge 0}\), \((v_n)_{n\ge 0}\) et \((w_n)_{n\ge 0}\) définies par \(u_0,v_0,w_0\) des réels donnés et pour \(n \ge 1\) : \((\mathtt{S})\left\{\begin{array}{rcc}u_n&=&u_{n-1}+2v_{n-1}+3w_{n-1}\\v_n&=&v_{n-1}+2w_{n-1}\\ w_n&=&w_{n-1} \\\end{array}\right.\)
Quelles sont les assertions vraies ?
Correction
Explication Générale
On a : \(N=\left(\begin{array}{rcc}0&2&3\\0&0&2\\ 0&0&0\\ \end{array}\right)\), \(N^2=\left(\begin{array}{rcc}0&0&4\\0&0&0\\ 0&0&0\\ \end{array}\right)\) et \(N^k=0, \) pour tout \(k\ge 3\). Comme \(A= N+I\) et le produit des matrices \(N\) et \(I\) est commutatif, on peut appliquer la formule du binôme pour le calcul des puissances de \(A\).
En calculant \(A^n\) et utilisant l'égalité : \(\left(\begin{array}{r}u_n\\v_n\\ w_n\\ \end{array}\right) = A^n \left(\begin{array}{r}u_0\\v_0\\ w_0\\ \end{array}\right)\), on déduit que : \(\left\{\begin{array}{rcc}u_n&=&u_0+2nv_0+n(2n+1)w_0\\v_n&=&v_0+2nw_0\\ w_n&=&w_0 \\\end{array}\right.\)
?MatriceS
Énoncé
On considère \({\cal F}\) l'espace vectoriel des fonctions réelles engendré par les fonctions \(f_1, \; f_2\) et \(f_3\) définies par : \(f_1(x)=1, \; f_2(x)=e^x\) et \(f_3(x)=xe^x\). Soit \(\phi\) l'application linéaire définie : \(\begin{array}{rccc}\phi:& {\cal F}&\to& {\cal F}\\& f&\to &f+f'-f'' \end{array}\), où \(f'\) (resp. \(f''\)) est la dérivée première (resp. seconde) de \(f\). On notera \(M\) la matrice de \(\phi\) dans la base \({\cal B}=\{f_1, f_2,f_3\}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
La matrice de \(\phi\) d'une base \( {\cal {B}}=(u_j)\) dans une base \( {\cal {B}}'=(v_i)\) est la matrice dont la \(j\)-ème colonne est constituée des coordonnées de \(\phi(u_j)\) dans la base \( {\cal {B}}'\). Donc \(M= \left(\begin{array}{rcc}1&0&0\\0&1&-1\\ 0&0&1\end{array}\right)\). Le rang d'une matrice est le nombre maximum de vecteurs colonnes ou lignes linéairement indépendants. Donc le rang de \(M\) est \(3\). Par conséquent, \(\phi\) est bijective et \(M\) est inversible. On vérifie que \(M^{-1} = \left(\begin{array}{rcc}1&0&0\\0&1&1\\ 0&0&1\end{array}\right)\).
?Fonction majorée/minorée (2)
Énoncé
Soient \(f,g : \mathbb{R} \to \mathbb{R}\). Quelles sont les assertions (ou propositions) vraies ?
Mais attention bornée signifie à la fois majorée et minorée
Correction
Explication Générale
La somme de deux fonctions majorées (resp. minorées) est majorée (resp. minorée). Ce n'est pas le cas pour le produit : par exemple \(f(x) = -1\) est minorée, \(g(x) = \exp(x)\) aussi, mais \(f \times g (x) = -\exp(x)\) ne l'est pas.
Pour aller plus loin :
cours : Limites et fonctions continues
video : Fonctions bornées
?Fonctions : domaine de définition (4)
Énoncé
Soient \(f : ]-\infty,0[ \to ]0,1[\) et \(g : ]-2,2[ \to ]0,+\infty[\). Quelles sont les assertions (ou propositions) vraies ?
Correction
Explication Générale
Si \(x \mapsto f(x)\) est définie sur \(]a,b[\) alors \(x \mapsto f(x+k)\) est définie sur \(]a-k,b-k[\) et \(x \mapsto f(\ell x)\) est définie sur \(]\frac{a}{\ell},\frac{b}{\ell}[\) (où \(\ell > 0\)).
Pour aller plus loin :
video : Notion sur les fonctions
?Fonctions - continuité en un point (3)
Énoncé
Parmi les propriétés suivantes, quelles sont celles qui impliquent que \(f\) est continue en \(x_ 0\) ?
Correction
Explication Générale
Si \(f(x)^2 \to f(x_0)^2\) alors ce n'est pas toujours vrai que \(f(x) \to f(x_0)\), prendre la fonction \(f(x)=-1\) si \(x < 0\) et \(f(x)=+1\) sinon. Par contre avec le cube c'est vrai, car la fonction \(x \mapsto x^3\) est une bijection continue de \(\mathbb{R}\) dans \(\mathbb{R}\), idem avec l'exponentielle.
Pour aller plus loin :
cours : Limites et fonctions continues
video : Continuité autour d'un point
exercices : Fonctions continues
?Fonctions - continuité en un point (4)
Énoncé
Soit \(f : \mathbb{R} \to \mathbb{R}\) une fonction et \((u_n)_{n\in\mathbb{N}}\) une suite. Quelles sont les assertions vraies ?
Correction
Explication Générale
Une fonction \(f\) est continue en \(\ell\) si et seulement si pour toute suite \((u_n)\) qui tend vers \(\ell\), on a \(f(u_n) \to f(\ell)\).
Pour aller plus loin :
video : Suites et continuité
?Fonctions - zéros de fonction (5)
Énoncé
Soit \(f : [a,b] \to \mathbb{R}\) une fonction continue (avec \(a < b\)). Quelles assertions sont vraies ?
Correction
Explication Générale
Le théorème des valeurs intermédiaires implique que si \(f : [a,b] \to \mathbb{R}\) est continue avec \(f(a) \cdot f(b) < 0\) alors il existe une valeur \(c \in [a,b]\) telle que \(f(c)=0\). Pour avoir l'unicité de ce zéro, il suffit que \(f\) soit strictement croissante ou bien strictement décroissante sur l'intervalle \( [a,b]\).
Pour aller plus loin :
video : Continuité en un point
video : Fonctions monotones
video : La bijection
exercices : Fonctions continues
?Fonction bijective (1)
Énoncé
Soit \(f : \mathbf{R} \to \mathbf{R}\) une fonction continue telle que : elle est strictement croissante sur \(]-\infty,0]\) ; strictement décroissante sur \([0,1]\) ; strictement croissante sur \([1,+\infty[\). En plus \(\lim_{x\to-\infty} f = - \infty\), \(f(0)=2\), \(f(1) = 1\) et \(\lim_{x\to+\infty} f = 3\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Le plus simple est de dessiner l'allure du graphe (ou le tableau de variation) pour se convaincre que \(f\) restreinte à \(]-\infty,0]\) définit une bijection vers \(]-\infty,2]\) ; \(f\) restreinte à \([0,1]\) définit une bijection (décroissante) vers \([1,2]\) ; \(f\) restreinte à \([1,+\infty[\) définit une bijection vers \([1,3[\).
Pour aller plus loin :
cours : Limites et fonctions continues
video : Continuité en un point
video : La bijection
exercices : Fonctions continues
?Fonction bijective (3)
Énoncé
Soit \(f : I \to J\) une fonction continue, où \(I\) et \(J\) sont des intervalles de \(\mathbf{R}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
La bijection réciproque d'une fonction continue est continue. En particulier cela implique que pour \(f^{-1} : J \to I\), si \(J\) est un intervalle fermé et borné, alors \(I\) aussi.
Pour aller plus loin :
cours : Limites et fonctions continues
video : La bijection
exercices : Fonctions continues
?Dérivée seconde ou plus (1)
Énoncé
Soit \(x\in R\setminus\{-1\} \) et soit \(\displaystyle f(x)=\frac{1}{1+x}\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On a \(\displaystyle f'(x)=\frac{-1}{(1+x)^2}\), \(\displaystyle f''(x)=\frac{2}{(1+x)^3}\) et l'on vérifie, par récurrence, que \(\forall n\in \mathbf{N}^*,\; f^{(n)}(x)=\frac{(-1)^nn!}{(1+x)^{n+1}}.\)
Pour aller plus loin :
cours : Dérivée d'une fonction
video : Définition de la dérivée
video : Théorème de Rolle
?Fonctions réelles - dérivée en un point (3)
Énoncé
Soit \(a,b\in \mathbf{R}\) et \(f(x)=\left\{\begin{array}{cl}\displaystyle \mathrm{e}^{x^2+x}&\mbox{si }x\leq 0\\ \\ a \arctan x+b &\mbox{si }x > 0.\end{array}\right.\) Quelles valeurs faut-il donner à \(a\) et \(b\) pour que \(f\) soit dérivable sur \(\mathbf{R}\) ?
Correction
Explication Générale
La fonction \(f\) est continue sur \(\mathbf{R}^*\) et pour qu'elle soit continue en \(0\), il faut que \(\lim _{x\to 0^-}f(x)=\lim _{x\to 0^+}f(x)\Rightarrow 1=b.\) De plus, \(f\) est dérivable sur \(\mathbf{R}^*\) avec \(f'(x)=\left\{\begin{array}{cl}\displaystyle (2x+1)\mathrm{e}^{x^2+x}&\mbox{si }x < 0\\ \\ \displaystyle \frac{a}{1+x^2} &\mbox{si }x > 0\end{array}\right.\) et \(f'_g(0)=1\) et \(f'_d(0)=a\). Donc, pour que \(f\) soit dérivable en \(0\), on doit avoir \(f'_g(0)=f'_d(0)\). D'où \(a=1\).
Pour aller plus loin :
cours : Dérivée d'une fonction
video : Définition de la dérivée
?Dérivabilité des fonctions réelles - fonction constante sur un intervalle
Énoncé
Soit \(f(x)=\arctan x+\arctan \frac{1}{x}\) définie sur \(\mathbf{R}^*\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
La fonction \(f\), tout comme la fonction \(\arctan\), est impaire. On calcule \(f'(x)\) pour \(x\neq 0\) : \(f'(x)=\frac{1}{1+x^2}+\frac{\left(\frac{1}{x}\right)'}{1+\left(\frac{1}{x}\right)^2}=0\) Donc \(f\) est constante sur chaque intervalle de son domaine de définition : \(f(x)=\left\{\begin{array}{ll} \displaystyle f(1)=\frac{\pi}{2} & \mbox{si }x > 0\\ f(-1)=-\frac{\pi}{2}&\mbox{si }x < 0.\end{array} \right.\)
Pour aller plus loin :
video : Fonctions paire et impaire
cours : Dérivée d'une fonction
video : Définition de la dérivée
video : Calculs fonction arctangente
?Dérivée sur un intervalle
Énoncé
Soit \(f\) une fonction continue sur \([-1,1]\) telle que \(f(0)=\pi\) et, pour tout \(x\in ]-1,1[\), \(\displaystyle f'(x)=\frac{1}{\sqrt{1-x^2}}\). Comment peut-on exprimer \(f\) ?
Correction
Explication Générale
On remarque que \(f'(x)=(\arcsin x)'=(-\arccos x)'\). Donc, \(\forall x\in [-1,1],\; f(x)=\arcsin x+C_1=-\arccos x+C_2.\) Mais \(f(0)=\pi \Rightarrow C_1=\pi\) et \(\displaystyle C_2=\frac{3\pi}{2}\).
?Dérivabilité des fonctions réelles - théorème de Rolle (4)
Énoncé
Soit \(f\) une fonction réelle continue sur \([a,b]\), dérivable sur \(]a,b[\) et telle que \(f(a)=f(b)=0\). Soit \(\alpha \notin [a,b]\) et \(\displaystyle g(x)=\frac{f(x)}{x-\alpha }\).
Correction
Explication Générale
La fonction \(g\) est continue sur \([a,b]\) et elle est dérivable sur \(]a,b[\) avec \(g'(x)=\frac{f'(x)(x-\alpha)-f(x)}{(x-\alpha)^2}.\) De plus \(g(a)=g(b)=0\). On peut donc appliquer le théorème de Rolle. Il existe alors \(c\in ]a,b[\) tel que \(g'(c)=0\Leftrightarrow f'(c)(c-\alpha)-f(c)=0\Leftrightarrow f'(c)=\frac{f(c)}{c-\alpha}.\) La tangente à la courbe représentative de \(f\) au point d'abscisse \(c\) a pour équation cartésienne \(y=f'(c)(x-c)-f(c).\) Cette tangente passe par le point de coordonnées \((\alpha ,0)\).
Pour aller plus loin :
cours : Dérivée d'une fonction
video : Définition de la dérivée
video : Définition de la tangente
video : Définition de la continuité
video : Calculs
?Dérivabilité des fonctions réelles - étude convexité (2)
Énoncé
Soit \(f\) la fonction logarithme népérien. Quelles sont les bonnes réponses ?
Correction
Explication Générale
On a \(\displaystyle f''(x)=-\frac{1}{x^2} < 0\). Donc \(f\) est concave sur \(\mathbf{R}^{+*}\). Ainsi, par définition, \(\forall t\in [0,1]\; \forall a,b\in \mathbf{R}^{+*},\; f\left[ta+(1-t)b\right]\geq tf(a)+(1-t)f(b).\) En prenant \(a=\mathrm{e}^x\) et \(b=\mathrm{e}^x\), où \(x,y\in \mathbf{R}\), on aura \(\ln\left[t\mathrm{e}^x+(1-t)\mathrm{e}^y\right]\geq tx+(1-t)y.\) Il suffit de composer par la fonction exponentielle, qui est strictement croissante, pour avoir \(t\mathrm{e}^x+(1-t)\mathrm{e}^y\geq \mathrm{e}^{tx+(1-t)y}.\)
Pour aller plus loin :
cours : Dérivée d'une fonction
video : Définition de la dérivée
video : Calculs
video : Extremum local
video : Théorème de Rolle
exercices : Fonctions dérivables
?Fonctions réelles : calcul de dérivée (6)
Énoncé
Soit \(f(x)=\arcsin (1-2x^2)\) définie sur \([-1,1]\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
La fonction \(f\) est clairement paire. On calcule \(f'(x)\) pour \(x\in ]0,1[\) : \(f'(x)=\frac{(1-2x^2)'}{\sqrt{1-(1-2x^2)^2}}=\frac{-2x}{|x|\sqrt{1-x^2}}.\) Donc, pour \(x\in ]0,1[\), \(\displaystyle f'(x)=\frac{-2}{\sqrt{1-x^2}}=(-2\arcsin x)'\). Ainsi, \(\forall x\in [0,1],\; f(x)=-2\arcsin x+C.\) Or \(\displaystyle f(0)=\arcsin 1=\frac{\pi}{2}=-2\arcsin 0+C\), donc \(\displaystyle C=\frac{\pi}{2}\). Par ailleurs, \(\left\{\begin{array}{l}f\mbox{ est continue sur }[0,1]\\ f\mbox{ est dérivable sur }]0,1[\\ \displaystyle \lim _{x\to 0^+}f'(x)=-2 \end{array}\right\}\Rightarrow f'_d(0)=-2.\) On vérifie, de même, que \(f'_g(0)=2\).
Pour aller plus loin :
cours : Dérivée d'une fonction
video : Définition de la dérivée
video : Fonctions paire et impaire
?Développements limités
Énoncé
Soit \(\displaystyle f(x)=(1+x)^{1/(\mathrm{e}^x-1)}\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
On a : \(\displaystyle f(x)=\mathrm{exp}\left(\frac{\ln (1+x)}{\mathrm{e}^x-1}\right)\). Donc, pour écrire le \(\displaystyle DL_2(0)f(x)\), on utilise le \(DL_3(0)\ln (1+x)\) et le \(DL_3(0)(\mathrm{e}^x-1)\). La division suivant les puissances croissantes donne \(DL_2(0)\frac{\ln (1+x)}{\mathrm{e}^x-1}=1-x+\frac{2x^2}{3}+o(x^2)\). Ensuite, avec \(\displaystyle \mathrm{e}^{1+u}=\mathrm{e}.\mathrm{e}^u=\mathrm{e}.\left(1+u+\frac{u^2}{2}+o(u^2)\right)\) où \(\displaystyle u=-x+\frac{2x^2}{3}+o(x^2)\), on obtient : \(f(x)=\mathrm{e}-\mathrm{e}.x+\frac{7\mathrm{e}}{6}x^2+o(x^2)\).
?Développements limités
Énoncé
Soit \(\displaystyle f(x)=\sqrt{x^2+x}-\sqrt{x^2-1}\). On considère la fonction \(g\) définie par \(\displaystyle g(t)=f\left(\frac{1}{t}\right)\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
On a : \(\displaystyle g(t)=\sqrt{\frac{1}{t^2}+\frac{1}{t}}-\sqrt{\frac{1}{t^2}-1}=\frac{\sqrt{1+t}-\sqrt{1-t^2}}{|t|}\). Donc, pour \(0 < t < 1\), \(\displaystyle g(t)=\frac{\sqrt{1+t}-\sqrt{1-t^2}}{t}\Rightarrow DL_2(0^+)g(t)=\frac{1}{2}+\frac{3t}{8}+\frac{t^2}{16}+o(t^2)\). Ainsi : \(\displaystyle DL_2(+\infty)f(x)=\frac{1}{2}+\frac{3}{8x}+\frac{1}{16x^2}+o\left(\frac{1}{x^2}\right)\). Pour \(-1 < t < 0\), \(\displaystyle g(t)=\frac{\sqrt{1+t}-\sqrt{1-t^2}}{-t}\Rightarrow DL_2(0^-)g(t)=-\frac{1}{2}-\frac{3t}{8}-\frac{t^2}{16}+o(t^2)\). D'où, \(\displaystyle DL_2(-\infty)f(x)=-\frac{1}{2}-\frac{3}{8x}-\frac{1}{16x^2}+o\left(\frac{1}{x^2}\right)\).
?Développements limités
Énoncé
Soit \(\displaystyle f(x)=\arctan\left(\frac{x}{x+1}\right)\). On considère la fonction \(g\) définie par \(\displaystyle g(t)=f\left(\frac{1}{t}\right)\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Pour \(0 < t\), on a : \(\displaystyle g(t)=\arctan\left(\frac{1}{1+t}\right)=\frac{\pi}{2}-\arctan (1+t)\) et \(g'(t)=\frac{-1}{1+(1+t)^2}=\frac{-1}{2}\times \frac{1}{1+(t+t^2/2)}=-\frac{1}{2}+\frac{t}{2}+o(t)\). Par intégration, et puisque \(\displaystyle \arctan 1=\frac{\pi}{4}\), on obtient : \(DL_2(0^+)g(t)=\frac{\pi}{4}-\frac{t}{2}+\frac{t^2}{4}+o(t^2)\Rightarrow DL_2(+\infty)f(x)=\frac{\pi}{4}-\frac{1}{2x}+\frac{1}{4x^2}+o\left(\frac{1}{x^2}\right)\).
?Développements limités
Énoncé
Soient \(f\) et \(g\) telles que \(\displaystyle f(x)=\frac{x^2}{x-1}\ln\left(\frac{x+1}{x}\right)\) et \(\displaystyle g(t)=f\left(\frac{1}{t}\right)\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
D'abord \(\displaystyle g(t)=\frac{\ln (1+t)}{t-t^2}=1+\frac{t}{2}+\frac{5t^2}{6}+o(t^2)\). Donc \(DL_2(+\infty)f(x)=1+\frac{1}{x}+\frac{5}{6x^2}+o\left(\frac{1}{x^2}\right)\).
?Développements limités
Énoncé
On considère les fonctions \(f\) et \(g\) telles que \(\displaystyle f(x)=x\arctan x\) et \(\displaystyle g(x)=xf\left(\frac{1}{x}\right)\). On note \(\Gamma\) le graphe de \(f\) et \(\Delta\) la droite d'équation \(\displaystyle y=\frac{\pi}{2}x-1\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
On a : \(\displaystyle g(x)=\arctan \frac{1}{x}=\frac{\pi}{2}-\arctan x\) si \(x > 0\) et \(\displaystyle g(x)=-\frac{\pi}{2}-\arctan x\) si \(x < 0\). Or, \(\displaystyle g'(x)=-\frac{1}{1+x^2}=-1+x^2+o(x^2)\). Donc, par intégration : \(DL_3(0^+)g(x)=\frac{\pi}{2}-x+\frac{x^3}{3}+o(x^3)\Rightarrow DL_2(+\infty)f(x)=\frac{\pi}{2}x-1+\frac{1}{3x^2}+o\left(\frac{1}{x^2}\right)\) et \(DL_3(0^-)g(x)=-\frac{\pi}{2}-x+\frac{x^3}{3}+o(x^3)\Rightarrow DL_2(-\infty)f(x)=-\frac{\pi}{2}x-1+\frac{1}{3x^2}+o\left(\frac{1}{x^2}\right)\). Ainsi, au voisinage de \(+\infty\), \(\Gamma\) admet \(\Delta\) comme asymptote et \(\Gamma\) est situé au dessus de \(\Delta\) car \(\displaystyle f(x)-y=\frac{1}{3x^2}+o\left(\frac{1}{x^2}\right)\geq 0\). Par contre, au voisinage de \(-\infty\), \(\Gamma\) admet la droite \(\Delta '\) d'équation \(\displaystyle y=-\frac{\pi}{2}x-1\) comme asymptote et \(\Gamma\) est situé au dessus de \(\Delta '\) car \(\displaystyle f(x)-y=\frac{1}{3x^2}+o\left(\frac{1}{x^2}\right)\geq 0\). Enfin, \(g\) n'admet pas de limite en \(0\) car \(\displaystyle \lim _{x\to 0^+}g(x)=\frac{\pi}{2}\) et \(\displaystyle \lim _{x\to 0^-}g(x)=-\frac{\pi}{2}\).
?Développements limités
Énoncé
On considère les fonctions \(f\) et \(g\) telles que \(\displaystyle f(x)=x^2\arctan \frac{1}{1+x^2}\) et \(\displaystyle g(x)=f\left(\frac{1}{x}\right)\). On note \(\Gamma\) le graphe de \(f\) et \(\Delta\) la droite d'équation \(\displaystyle y=1\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
On a : \(\displaystyle g(x)=\frac{1}{x^2}\arctan \frac{x^2}{1+x^2}\). On vérifie que \(\displaystyle DL_4(0)\arctan u=u-\frac{u^3}{3}+o(u^4)\) et donc avec \(\displaystyle u=\frac{x^2}{1+x^2}=x^2-x^4+o(x^4)\), on obtient : \(DL_2(0)g(x)=1-x^2+o(x^2) \Rightarrow DL_2(\pm\infty)f(x)=1-\frac{1}{x^2}+o\left(\frac{1}{x^2}\right)\). Ainsi, au voisinage de \(\pm\infty\), \(\Gamma\) admet \(\Delta\) comme asymptote et \(\Gamma\) est situé en dessous de \(\Delta\) car \(\displaystyle f(x)-y=-\frac{1}{x^2}+o\left(\frac{1}{x^2}\right)\leq 0\). Enfin, \(\displaystyle \lim _{x\to 0^+}g(x)=\lim _{x\to 0^-}g(x)=1\).
?Développements limités
Énoncé
Soit \(\displaystyle f(x)=x\arctan \left(\frac{1}{\sqrt{1+x^2}}\right)\). On considère la fonction \(g\) telle que \(\displaystyle g(x)=f\left(\frac{1}{x}\right)\) et on note \(\Gamma\) le graphe de \(f\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
On a : \(\displaystyle g(x)=\frac{1}{x}\arctan \left(\frac{x}{\sqrt{1+x^2}}\right)\) si \(x > 0\) et \(\displaystyle g(x)=\frac{-1}{x}\arctan \left(\frac{x}{\sqrt{1+x^2}}\right)\) si \(x < 0\). Dans le \(DL_3(0)\arctan u\), on pose \(\displaystyle u=\frac{x}{\sqrt{1+x^2}}=x-\frac{x^3}{2}+o(x^3)\). Ceci donne : \(DL_2(0^+)g(x)=1-\frac{5x^2}{6}+o(x^2)\Rightarrow DL_2(+\infty)f(x)=1-\frac{5}{6x^2}+o\left(\frac{1}{x^2}\right)\) et \(DL_2(0^-)g(x)=-1+\frac{5x^2}{6}+o(x^2)\Rightarrow DL_2(-\infty)f(x)=-1+\frac{5}{6x^2}+o\left(\frac{1}{x^2}\right).\) Ainsi \(\Gamma\) admet la droite d'équation \(\displaystyle y=1\) (resp. \(y=-1\)) comme asymptote au voisinage de \(+\infty\) (resp. \(-\infty\)). Enfin, \(g\) n'admet pas de limite en \(0\) car \(\displaystyle \lim _{x\to 0^+}g(x)=1\) et \(\displaystyle \lim _{x\to 0^-}g(x)=-1\).
?Développements limités
Énoncé
On considère les fonctions \(f\) et \(g\) telles que \(\displaystyle f(x)=\sqrt{x^2+1}\mathrm{e}^{1/(x+1)}\) et \(\displaystyle g(x)=xf\left(\frac{1}{x}\right)\). On note \(\Gamma\) le graphe de \(f\) et \(\Delta\) la droite d'équation \(y=x+1\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
On a : \(\displaystyle g(x)=\sqrt{1+x^2}\mathrm{e}^{x/(1+x)}\) si \(x > 0\) et \(\displaystyle g(x)=-\sqrt{1+x^2}\mathrm{e}^{x/(1+x)}\) si \(x < 0\). On calcule le \(DL_3(0)\sqrt{1+x^2}\mathrm{e}^{x/(1+x)}\). Ce qui donne : \(DL_3(0^+)g(x)=1+x+\frac{2}{3}x^3+o(x^3)\Rightarrow DL_2(+\infty)f(x)=x+1+\frac{2}{3x^2}+o\left(\frac{1}{x^2}\right)\) et \(DL_3(0^-)g(x)=-1-x-\frac{2}{3}x^3+o(x^2)\Rightarrow DL_2(-\infty)f(x)=-x-1-\frac{2}{3x^2}+o\left(\frac{1}{x^2}\right)\). Ainsi, au voisinage de \(+\infty\), \(\Gamma\) admet \(\Delta\) comme asymptote et \(\Gamma\) est situé au dessus de \(\Delta\) car \(\displaystyle f(x)-y=\frac{2}{3x^2}+o\left(\frac{1}{x^2}\right)\geq 0\). Mais, au voisinage de \(-\infty\), \(\Gamma\) admet la droite \(\Delta '\) d'équation \(y=-x-1\) comme asymptote, et \(\Gamma\) est situé en dessous de \(\Delta '\) car \(\displaystyle f(x)-y=-\frac{2}{3x^2}+o\left(\frac{1}{x^2}\right)\leq 0\). Enfin, \(g\) n'admet pas de limite en \(0\) car \(\displaystyle \lim _{x\to 0^+}g(x)=1\) et \(\displaystyle \lim _{x\to 0^-}g(x)=-1\).
?Équations différentielles du premier ordre
Énoncé
On considère l'équation différentielle \((E)\) : \((x+1)y'+y=2x+1\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Remarquer que \(y_0=x\) est une solution particulière. Donc la solution générale de \((E)\) sur \(]-1,+\infty[\), ou \(]-\infty,-1[\), est : \(\displaystyle y=x+\frac{k}{x+1}\), \(k\in \mathbb{R}\). Si \(y\) est une solution de \((E)\) sur \(\mathbb{R}\), alors \(y\) est une solution de \((E)\) sur \(]-1,+\infty[\) et \(y\) est une solution de \((E)\) sur \(]-\infty,-1[\). De plus, avec \(x=-1\) dans \((E)\), on aura \(y(-1)=-1\). D'où \(y(x)=\left\{\begin{array}{lll}\displaystyle y(x)=x+\frac{k_1}{x+1}&\mbox{si}&x\in ]-1,+\infty [ \\\\ \displaystyle y(x)=x+\frac{k_2}{x+1}&\mbox{si}&x\in ]-\infty ,-1[\\ -1&\mbox{si}&x=-1 \end{array}\right.\)
La continuité de \(y\) en \(-1\) implique que \(k_1=k_2=0\). L'équation \((E)\) ne possède qu'une seule solution sur \(\mathbb{R}\).
?Équations différentielles du premier ordre
Énoncé
On considère l'équation différentielle \((E)\) : \((1-x^2)y'-(1+x)y=1\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
La solution générale de l'équation homogène sur l'un de ces intervalles est \(\displaystyle y=\frac{k}{1-x}\), \(k\in \mathbb{R}\). La variation de la constante implique que \(\displaystyle y_0=\frac{\ln |1+x|}{1-x}\) est une solution particulière. En posant \(x=-1\) dans \((E)\), on obtient \(0=1\) ce qui est absurde. Donc \((E)\) n'admet pas de solution ni sur \(\mathbbf{R}\) ni sur \(]-\infty ,1[\).
Si \(y\) est une solution sur \(]-1,+\infty [\), on aura : \(y(x)=\left\{\begin{array}{lll}\displaystyle \frac{k_1+\ln (1+x)}{1-x}&\mbox{si}&x\in ]-1,1[ \\ \\ \displaystyle \frac{k_2+\ln (1+x)}{1-x}&\mbox{si}&x\in ]1,+\infty[ \end{array}\right.\) et \(y(1)=-1/2\)
La continuité en \(1\) implique que \(k_1=k_2=-\ln 2\). Une telle fonction est aussi dérivable en \(1\). Ainsi \((E)\) admet une unique solution sur \(]-1,+\infty [\).
?Équations différentielles du premier ordre
Énoncé
On considère l'équation différentielle \((E)\) : \(x(1-x)y'+y=x\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Si \((E)\) admet une solution \(y\) sur \(]-\infty ,1[\), on aura : \(y(x)=\left\{\begin{array}{lll}\displaystyle \frac{k_1(x-1)}{x}+\frac{1-x}{x}\ln |1-x|+\frac{1}{x}&\mbox{si}&x\in ]-\infty ,0[ \\ \\ \displaystyle \frac{k_2(x-1)}{x}+\frac{1-x}{x}\ln |1-x|+\frac{1}{x}&\mbox{si}&x\in ]0,1[ \end{array}\right.\) et \(y(0)=0\).
La continuité de \(y\) en \(0\), implique que \(k_1=k_2=1\). De plus, une telle fonction est dérivable en \(0\). Ainsi \((E)\) admet une unique solution sur \(]-\infty ,1[\). De même, si \((E)\) admet une solution \(y\) sur \(]0,+\infty [\), on aura : \(y(x)=\left\{\begin{array}{lll}\displaystyle \frac{k_1(x-1)}{x}+\frac{1-x}{x}\ln |1-x|+\frac{1}{x}&\mbox{si}&x\in ]0,1[ \\ \\ \displaystyle\frac{k_2(x-1)}{x}+\frac{1-x}{x}\ln |1-x|+\frac{1}{x}&\mbox{si}&x\in ]1,+\infty[ \end{array}\right.\) et \(y(1)=1\).
Une telle fonction est continue en \(1\) mais elle n'est pas dérivable en \(1\). Ainsi \((E)\) n'admet pas de solution sur \(]0,+\infty [\).
?Équations différentielles du second ordre
Énoncé
On considère les équations différentielles \((E_1)\; :\; xy''+2(x+1)y'+(x+2)y=2\mathrm{e}^{-x}\quad\mbox{et}\quad (E_2)\; :\; y''+2y'+y=2\mathrm{e}^{-x}\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
On a : \(z'=xy'+y\), \(z''=xy''+2y'\) et \(z''+2z'+z=xy''+2(x+1)y'+(x+2)y\), donc si \(y\) est une solution de \((E_1)\), alors \(\displaystyle z=xy\) est une solution de \((E_2)\). La solution générale de l'équation homogène associée à \((E_2)\) est : \(Z=(ax+b)\mathrm{e}^{-x}\) et \(z_0=x^2\mathrm{e}^{-x}\) est une solution particulière de \((E_2)\). Donc la solution générale de \((E_2)\) est \(z=Z+z_0\). Ainsi, la solution générale de \((E_1)\) sur \(]0,+\infty[\) est : \(\displaystyle y=\left(x+a+\frac{b}{x}\right)\mathrm{e}^{-x}\), \(a,b\in \mathbb{R}\). Une telle solution se prolonge par continuité en \(0\) si et seulement si \(b=0\).
?Équations différentielles du second ordre
Énoncé
On considère les équations différentielles \((E_1)\; :\; xy''+2y'-xy=2\mathrm{e}^{x}\quad\mbox{et}\quad (E_2)\; :\; z''-z=2\mathrm{e}^{x}\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
On a : \(z'=xy'+y\), \(z''=xy''+2y'\) et \(z''-z=xy''+2y'-xy\), donc si \(y\) est une solution de \((E_1)\), alors \(\displaystyle z=xy\) est une solution de \((E_2)\). La solution générale de l'équation homogène associée à \((E_2)\) est : \(Z=a\mathrm{e}^{x}+b\mathrm{e}^{-x}\) et \(z_0=x\mathrm{e}^{x}\) est une solution particulière de \((E_2)\). Donc la solution générale de \((E_2)\) est \(z=Z+z_0\). Ainsi, la solution générale de \((E_1)\) sur \(]0,+\infty[\) est : \(\displaystyle y=\left(\frac{a}{x}+1\right)\mathrm{e}^{x}+\frac{b}{x}\mathrm{e}^{-x}\), \(a,b\in \mathbb{R}\). Une telle solution se prolonge par continuité en \(0\) si et seulement si \(a=b=0\). D'où \(\displaystyle y=\mathrm{e}^{x}\). Réciproquement, on vérifie qu'une telle fonction est bien une solution de \((E_1)\) sur \(\mathbb{R}\).
?Ensembles, applications
Énoncé
Soient \(E\) et \(F\) deux ensembles non vides et \(f\) une application de \(E\) dans \(F\). Soient \(A,B\) deux sous-ensembles de \(E\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On a : \(y\in f(A\cup B)\Leftrightarrow \exists x\in A\cup B,\; y=f(x)\Leftrightarrow (\exists x\in A,\; y=f(x))\mbox{ ou }(\exists x\in B,\; y=f(x))\Leftrightarrow (y\in f(A)\mbox{ ou }y\in f(B)).\)
Par ailleurs, si \(y\in f(A\cap B)\), il existe \(x\in A\cap B\) tel que \(y=f(x)\). Donc \(y\in f(A)\) et \(y\in f(B)\), c'est-à-dire \(y\in f(A)\cap f(B)\).
Pour aller plus loin :
cours : Ensembles et applications
video : Ensembles
video : Applications
?Fonctions usuelles - Domaine de définition (2)
Énoncé
Soit \( f(x)= \sqrt{\frac{1-x}{2-x}} \) et \(g(x)=\frac{\sqrt{1-x}}{\sqrt{2-x}}\). On notera \(D_f\) et \(D_g\) le domaine de définition de \(f\) et \(g\) respectivement. Quelles sont les assertions vraies ?
Correction
Explication Générale
\(f\) est définie si \(x\neq 2\) et \(\frac{1-x}{2-x}\ge 0\). On déduit que \(D_f=]-\infty, 1] \cup ]2,+\infty[\). \(g\) est définie si \(1-x \ge 0\) et \(2-x > 0\), c'est-à-dire \(x\le 1\).
Pour aller plus loin :
video : Notion sur les fonctions
?Fonctions usuelles - inéquation
Énoncé
Soit \((E)\) l'inéquation : \( \ln |1+x|-\ln |2x+1| \le \ln 2\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Soit \(x \in \mathbf{R} \backslash \{-1, -\frac{1}{2}\}\). \((E) \Leftrightarrow \ln \vert \frac{x+1}{4x+2} \vert \le 0 \Leftrightarrow \, (E') : \, \vert \frac{x+1}{4x+2} \vert \le 1 \). Si \(x > -\frac{1}{2}\), \((E')\Leftrightarrow -4x-2 \le x+1\le 4x+2 \Leftrightarrow x \ge -\frac{1}{3}\). Si \(x < -\frac{1}{2}\), \((E')\Leftrightarrow -4x-2 \ge x+1 \ge 4x+2 \Leftrightarrow x \le -\frac{3}{5}\). Par conséquent, l'ensemble des solutions de \((E)\) est \(]-\infty, -1[ \cup ]-1,-\frac{3}{5}] \cup [-\frac{1}{3}, + \infty[\).
Pour aller plus loin :
video : Logarithme Népérien
?Fonctions usuelles - étude de fonction (4)
Énoncé
Soit \(f(x)= \arctan x + \arctan (\frac{1}{x})\). Quelles sont les assertions vraies ?
Correction
Explication Générale
\(f\) est définie sur \(\mathbf{R}^*\), dérivable sur \(\mathbf{R}^*\) et \(f'(x)=0\), \(\forall x \in \mathbf{R}^*\). Puisque \(\mathbf{R}^* =]-\infty,0[\cup ]0,+\infty[\), \(f\) est constante sur chaque intervalle. Or \(f(1)=\frac{\pi}{2}\) et \(f(-1)=-\frac{\pi}{2}\), on déduit que \(f(x)=\left\{\begin{array}{cc}\frac{\pi}{2},& \mbox{si} \, \, x > 0 \\ -\frac{\pi}{2},& \mbox{si} \, x < 0 \end{array}\right.\).
Pour aller plus loin :
video : Fonctions circulaires inverses
exercices : Fonctions circulaires et hyperboliques inverses
?Fonctions usuelles - étude de fonction (6)
Énoncé
Soit \(f(x)=x+ \sqrt{ 1-x^2}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
\(f\) est définie sur \([-1,1]\), dérivable sur \(]-1,1[\) et \(f'(x)= 1-\frac{x}{\sqrt{1-x^2}}\). En étudiant les variations de \(f\), on déduit que \(f\) établit une bijection de \([-1,\frac{1}{\sqrt 2}]\) dans \([-1,\sqrt 2]\) et de \([\frac{1}{\sqrt 2}, 1]\) dans \([1,\sqrt 2]\). On peut aussi résoudre l'équation d'inconnue \(x\),\(y=f(x)\).
Pour aller plus loin :
cours : Fonctions usuelles
video : Fonctions monotones
video : Notion sur les fonctions
video : Logarithme Népérien
video : Exponentielle
video : Fonctions circulaires inverses
video : La bijection
exercices : Fonctions circulaires et hyperboliques inverses
?Fonctions usuelles - équation trigonométrique (1)
Énoncé
Soit \((E)\) l'équation : \( \cos 2x = \sin x. \)On note \(\cal{S}\) l'ensemble des solutions de \((E).\) Quelles sont les assertions vraies ?
Correction
Explication Générale
\((E) \Leftrightarrow \cos 2x = \cos ( \frac{\pi}{2} -x) \Leftrightarrow \exists k\in \mathbf{Z}; \, 2x = \frac{\pi}{2} -x +2k\pi \, \mbox {ou} \, 2x = -\frac{\pi}{2} +x +2k\pi \Leftrightarrow \exists k\in \mathbf{Z};\, x = \frac{\pi}{6} +\frac{ 2k\pi}{3} \, \mbox {ou} \, x = -\frac{\pi}{2} +2k\pi\). Donc \({\cal{S}} = \{\frac{\pi}{6} +\frac{ 2k\pi}{3}, \, k\in \mathbf{Z} \} \cup \{ -\frac{\pi}{2} +2k\pi, \, k\in \mathbf{Z} \}.\)
Pour aller plus loin :
video : Fonctions circulaires inverses
?Fonctions usuelles - équation trigonométrique (2)
Énoncé
Soit \(f\) une fonction solution de l'équation \((E)\) : \( \arcsin f(x) + \arcsin x = \frac{\pi}{2}\). on notera \(D_f\) le domaine de définition de \(f\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Pour aller plus loin :
video : Fonctions circulaires inverses
?Fonctions usuelles - trigonométrie (3)
Énoncé
Soit \(f(x)= \arcsin (\frac{2x}{1+x^2})\). On notera \(D_f\) le domaine de définition de \(f\). Quelles sont les assertions vraies ?
Correction
Explication Générale
\(f\) est définie si \(-1\le \frac{2x}{1+x^2} \le 1 \), c'est-à-dire \(-1-x^2 \le 2x \le 1+x^2\), ce qui revient à : \((x+1)^2\ge 0\) et \((x-1)^2\ge 0\), ce qui est le cas pour tout \(x \in \mathbf{R}\). \(f\) est dérivable sur \(\mathbf{R} \backslash \{-1,1\}\) et \(f'(x) = \frac{2(1-x^2)}{|1-x^2|(1+x^2)} = \left\{\begin{array}{cc}\frac{2}{1+x^2},& \mbox{si} \, -1 < x < 1 \\ -\frac{2}{1+x^2},& \mbox{si} \, x > 1 \, \mbox{ou} \, x < -1 \end{array}\right. \). Comme \(f\) est continue sur \(\mathbf{R}\), on déduit que : \(f(x)= \left\{\begin{array}{ccc}2\arctan x + c_1, & \mbox{si} \, -1\le x\le 1 \\ -2\arctan x + c_2, & \mbox{si} \, x\le -1 \\ -2\arctan x + c_3, & \mbox{si} \, x\ge 1 \end{array}\right.\), où \(c_1, c_2\) et \(c_3\) sont des constantes. En identifiant en \(0\), en \(-\infty\) et en \(+\infty\), on obtient : \(f(x)= \left\{\begin{array}{ccc}2\arctan x, & \mbox{si} \, -1\le x\le 1 \\ -2\arctan x -\pi, & \mbox{si} \, x\le -1 \\ -2\arctan x +\pi, & \mbox{si} \, x\ge 1 \end{array}\right.\).
Pour aller plus loin :
video : Fonctions circulaires inverses
?Fonctions usuelles - trigonométrie (4)
Énoncé
Soit \(f(x)= \arccos (\frac{1-x^2}{1+x^2})\). On notera \(D_f\) le domaine de définition de \(f\). Quelles sont les assertions vraies ?
Correction
Explication Générale
\(f\) est définie si \(-1\le \frac{1-x^2}{1+x^2} \le 1 \), ce qui est le cas pour tout \(x \in \mathbf{R}\). \(f\) est dérivable sur \(\mathbf{R}^*\) et \(f'(x) = -\frac{2x}{|x|(1+x^2)} =\left\{\begin{array}{cc}-\frac{2}{1+x^2},& \mbox{si} \, x > 0 \\ \frac{2}{1+x^2},& \mbox{si} \, x < 0 \end{array}\right. \). Comme \(f\) est continue sur \(\mathbf{R}\), on déduit que : \(f(x)= \left\{\begin{array}{cc}-2\arctan x + c_1, & \mbox{si} \, x\ge 0 \\ 2\arctan x + c_2, & \mbox{si} \, x\le 0 \end{array}\right. \), où \(c_1\) et \( c_2\) sont des constantes. En identifiant en \(+\infty\) et en \(-\infty\), on obtient : \(f(x)= \left\{\begin{array}{cc}-2\arctan x+2\pi, & \mbox{si} \, x\ge 0 \\ 2\arctan x +2\pi, & \mbox{si} \, x\le 0 \end{array}\right.\). Donc \(f(x) = -2\arctan |x|+2\pi, \, \forall x \in \mathbf{R}\).
Pour aller plus loin :
video : Fonctions circulaires inverses
?Fonctions usuelles - trigonométrie (5)
Énoncé
Soit \(f(x)= \arcsin (\sin x) + \arccos (\cos x)\). On notera \(D_f\) le domaine de définition de \(f\). Quelles sont les assertions vraies ?
Correction
Explication Générale
\(D_f=\mathbf{R}\). \(f\) est périodique de période \(2\pi\). En simplifiant \(f\) sur \([-\pi, \pi]\), on obtient : \(f(x) = \left\{\begin{array}{cccc}2x,& \mbox{si} \, 0\le x \le \frac{\pi}{2} \\ \pi ,& \mbox{si} \,\frac{\pi}{2} \le x \le \pi \\ 0 ,& \mbox{si} \,-\frac{\pi}{2} \le x \le 0 \\ -\pi-2x ,& \mbox{si} \, -\pi \le x \le - \frac{\pi}{2} \end{array}\right.\).
Pour aller plus loin :
video : Fonctions circulaires inverses
?Fonctions usuelles - étude de fonction (5)
Énoncé
Soit \(f(x)= \exp ( \frac{\ln^2 |x|}{\ln^2 |x|+1})\). On notera \(D_f\) le domaine de définition de \(f\). Quelles sont les assertions vraies ?
Correction
Explication Générale
\(D_f= \mathbf{R}^*\). Pour tout \(x\in \mathbf{R}^*\), \(f(-x)=f(x)\), donc \(f\) est paire. \(f\) est dérivable sur \(\mathbf{R}^*\). Si \(x > 0\), \(f'(x)= \frac{2\ln x}{x(\ln^2x+1)^2}f(x)\). En étudiant les variations de \(f\), on déduit que \(f\) est n'est pas monotone sur \(]0,+\infty[\) et qu'elle établit une bijection de \(]0,1]\) dans \([1,e[\) et de \([1,+\infty[\) dans \([1,e[\).
Pour aller plus loin :
video : Fonctions monotones
video : La bijection
video : Logarithme Népérien
video : Exponentielle
?Fonctions usuelles - étude de fonction (6)
Énoncé
Soit \(f(x)= x^x(1-x)^{1-x}\). On notera \(D_f\) le domaine de définition de \(f\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Par définition, \(f(x)= \exp [x\ln x + (1-x)\ln (1-x)]\), on déduit que \(D_f=]0,1[\). \(f\) est dérivable sur \(]0,1[\) et \(f'(x)= \ln (\frac{x}{1-x}) f(x)\). En étudiant les variations de \(f\), \(f\) n'est pas monotone sur \(]0,1[\). Elle établit une bijection de \(]0,\frac{1}{2}]\) dans \([\frac{1}{2},1[\) et de \([\frac{1}{2},1[ \) dans \([\frac{1}{2},1[\).
Pour aller plus loin :
video : Fonctions monotones
video : La bijection
video : Logarithme Népérien
video : Exponentielle
?Fonctions usuelles - étude de fonction (7)
Énoncé
Soit \(f(x)= (1+\frac{1}{x})^x\). Quelles sont les assertions vraies ?
Correction
Explication Générale
Par définition, \(f(x)= \exp [x\ln (1+\frac{1}{x})]\), on déduit que \(f\) est définie si \(x\in ]-\infty, -1[\cup ]0,+\infty[\). \(f\) est dérivable sur son domaine de définition et \(f'(x)= [\ln (1+\frac{1}{x}) - \frac{1}{x+1}] f(x)\). En étudiant les variations de la fonction \(x \mapsto \ln (1+\frac{1}{x}) - \frac{1}{x+1}\), on déduit les variations de \(f\). En particulier, \(f\) est croissante sur \(]-\infty, -1[\) et sur \(]0,+\infty[\), \(f(]-\infty, -1[)= ]e,+\infty[\) et \(f(]0, +\infty[)= ]1,e[\).
Pour aller plus loin :
video : Fonctions monotones
video : La bijection
video : Logarithme Népérien
video : Exponentielle
?Géométrie du plan - base orthonormée
Énoncé
Dans le plan muni d'un repère orthonormé direct \((O,\vec{i},\vec{j})\), on considère les vecteurs \(\displaystyle \vec{u}=\left(\frac{1}{2},a\right)\) et \(\displaystyle \vec{v}=\left(-\frac{\sqrt{3}}{2},b\right)\). Comment choisir les réels \(a\) et \(b\) pour que \((\vec{u},\vec{v})\) soit une base orthonormée directe ?
Correction
Explication Générale
D'abord, \(\displaystyle \|\vec{u}\|=1\Leftrightarrow a=\frac{\pm \sqrt{3}}{2}\), \(\displaystyle \|\vec{v}\|=1\Leftrightarrow b=\frac{\pm 1}{2}\) et \(\vec{u}\cdot\vec{v}=0\) si, et seulement si, \(a\) et \(b\) sont de même signe. Enfin pour que \((\vec{u},\vec{v})\) soit directe, il faut que \(\mbox{det}(\vec{u},\vec{v})\) soit positif.
Pour aller plus loin :
exercices : Droites du plan ; droites et plans de l'espace
?Intégration par parties
Énoncé
Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
D'abord \(\displaystyle \int \frac{\mathrm{d}x}{\sqrt{1-x^2}}=\arcsin (x)+k\), \(k\in \mathbb{R}\). Une intégration par parties avec \(u=\sqrt{1-x^2}\) et \(v=x\) donne \(\int \sqrt{1-x^2}\mathrm{d}x=x\sqrt{1-x^2}-\int \frac{-x^2\mathrm{d}x}{\sqrt{1-x^2}}\). Ensuite, en écrivant \(\displaystyle -x^2=(1-x^2)-1\), on obtient : \(\int \sqrt{1-x^2}\mathrm{d}x=x\sqrt{1-x^2}-\int \sqrt{1-x^2}\mathrm{d}x+\int \frac{\mathrm{d}x}{\sqrt{1-x^2}}\). D'où : \(\displaystyle 2\int \sqrt{1-x^2}\mathrm{d}x=x\sqrt{1-x^2}+\arcsin x+k\).
?Intégration par parties
Énoncé
Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Avec \(\displaystyle t=\sqrt{x}\), on a : \(\displaystyle x=t^2\Rightarrow \mathrm{d}x=2t\, \mathrm{d}t\) et \(\displaystyle \int \frac{\mathrm{d}x}{\sqrt{x}(x+1)^2}=\int \frac{2\, \mathrm{d}t}{(t^2+1)^2}\). Une intégration par parties avec \(\displaystyle u=\frac{1}{t^2+1}\) et \(v=t\) donne \(\int \frac{\mathrm{d}t}{t^2+1}=\frac{t}{t^2+1}+\int \frac{2t^2\, \mathrm{d}t}{(t^2+1)^2}=\frac{t}{t^2+1}+\int \frac{2\, \mathrm{d}t}{t^2+1}-\int \frac{2\, \mathrm{d}t}{(t^2+1)^2}\). D'où \(\displaystyle \int \frac{2\, \mathrm{d}t}{(t^2+1)^2}=\frac{t}{t^2+1}+\arctan t+k\Rightarrow \int \frac{\mathrm{d}x}{\sqrt{x}(x+1)^2}=\frac{\sqrt{x}}{x+1}+\arctan \sqrt{x}+k\), \(k\in \mathbb{R}\).
?Intégrale définie
Énoncé
On pose \(\displaystyle I=\int _0^{\pi}\mathrm{e}^x\cos ^2x\mathrm{d}x\), \(\displaystyle J=\int _0^{\pi}\mathrm{e}^x\sin ^2x\mathrm{d}x\) et \(\displaystyle K=\int _0^{\pi}\mathrm{e}^x\cos (2x)\mathrm{d}x\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Deux intégrations par parties successives, avec \(u=\cos (2x)\) et \(v=\mathrm{e}^x\) et ensuite avec \(u=\sin (2x)\) et \(v=\mathrm{e}^x\), donnent \(K=\mathrm{e}^{\pi}-1+2\int _0^{\pi} \mathrm{e}^x\sin (2x)\mathrm{d}x=\mathrm{e}^{\pi}-1-4K\Rightarrow K=\frac{\mathrm{e}^{\pi}-1}{5}\). A l'aide des relations \(\cos ^2x+\sin ^2x=1\) et \(\cos ^2x-\sin ^2x=\cos (2x)\), on obtient : \(I+J=\mathrm{e}^{\pi}-1\mbox{ et }I-J=K\Rightarrow I=\frac{3(\mathrm{e}^{\pi}-1)}{5}\quad \mbox{et}\quad J=\frac{2(\mathrm{e}^{\pi}-1)}{5}\).
?Intégrale définie
Énoncé
Soit \(f\) la fonction définie par \(\displaystyle f(x)=\frac{1}{(4+x^2)^2}\). On pose \(\displaystyle I=\int _0^2f(x)\,\mathrm{d}x\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Pour tout \(x\in [0,2]\), on a : \(\displaystyle \frac{1}{8^2}\leq f(x)\leq \frac{1}{4^2}\). Donc \(\displaystyle \frac{2}{8^2}\leq I\leq \frac{2}{4^2}\).
Le changement de variable \(x=2t\) donne \(\displaystyle I=\int _0^1\frac{2\mathrm{d}t}{(4+4t^2)^2}=\frac{2}{4^2}\int _0^1\frac{\mathrm{d}t}{(1+t^2)^2}\).
En intégrant \(\displaystyle \int _0^1\frac{\mathrm{d}t}{1+t^2}\) par parties avec \(\displaystyle u=\frac{1}{1+t^2}\) et \(v=t\), on obtient : \(\int _0^1\frac{\mathrm{d}t}{(1+t^2)^2}=\frac{1}{2}\left(\left[\frac{t}{1+t^2}\right]_0^1+\int _0^1\frac{\mathrm{d}t}{1+t^2}\right)=\frac{2+\pi}{8} \Rightarrow I=\frac{2+\pi}{64}\).
?Intégrale définie
Énoncé
Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Avec \(\displaystyle t=\sqrt{\frac{1+x}{1-x}}\), on a : \(\displaystyle x=\frac{t^2-1}{t^2+1}\). D'où \(\displaystyle \mathrm{d}x=\frac{4t\, \mathrm{d}t}{(t^2+1)^2}\) et \(\int _0^{1/2}\sqrt{\frac{1+x}{1-x}}\mathrm{d}x=\int _1^{\sqrt{3}}\frac{4t^2\, \mathrm{d}t}{(t^2+1)^2}\). Une intégration par parties avec \(\displaystyle u=\frac{1}{t^2+1}\) et \(v=t\) donne \(\int _1^{\sqrt{3}}\frac{\mathrm{d}t}{t^2+1}=\left[\frac{t}{1+t^2}\right]_1^{\sqrt{3}}+\int _1^{\sqrt{3}}\frac{2t^2\mathrm{d}t}{(t^2+1)^2}\). Donc \(\displaystyle \int _0^{1/2}\sqrt{\frac{1+x}{1-x}}\mathrm{d}x=2\int _1^{\sqrt{3}}\frac{\mathrm{d}t}{t^2+1}-2\left[\frac{t}{1+t^2}\right]_1^{\sqrt{3}}=\frac{\pi}{6}-\frac{\sqrt{3}}{2}+1\).
?Primitives des éléments simples
Énoncé
Soit \(n\in \mathbb{N}^*\). On note \(\displaystyle F_n(x)=\int _0^x\frac{\mathrm{d}t}{(t^2+1)^n}\) et \(\displaystyle I_n=\int _1^{\mathrm{e}}\frac{\mathrm{d}x}{x\left(\ln ^2x+1\right)^n}\). Parmi les affirmations suivantes, cocher celles qui sont vraies :
Correction
Explication Générale
Une intégration par parties, avec \(\displaystyle u=(t^2+1)^{-n}\) et \(v=t\), donne \(F_n(x)=\frac{x}{(x^2+1)^n}+2n\int _0^x \frac{t^2}{(t^2+1)^{n+1}}\mathrm{d}t\). En écrivant \(t^2=(t^2+1)-1\), on obtient : \(\displaystyle F_n(x)=\frac{x}{(x^2+1)^n}+2nF_n(x)-2nF_{n+1}(x)\). D'où \(F_{n+1}(x)=\frac{1}{2n}\left[\frac{x}{(x^2+1)^n}+(2n-1)F_n(x)\right]\). En particulier, comme \(F_1(x)=\arctan x\) on en déduit que \(\displaystyle F_2(x)=\frac{1}{2}\left[\frac{x}{x^2+1}+\arctan x\right]\). Le changement de variable \(t=\ln x\) donne \(I_n=F_n(1)\). On en déduit que \(\displaystyle I_1=\arctan 1=\frac{\pi}{4}\) et \(\displaystyle I_2=\frac{1}{4}+\frac{\pi}{8}\).
?Limites des fonctions réelles
Énoncé
Soit \(f(x)= \frac{\sqrt x}{\sqrt{x+\sqrt{x}}}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
\(f(x)= \frac{1}{\sqrt{1+\frac{1}{\sqrt{x}}}}.\)
Pour aller plus loin :
exercices : Limites de fonctions
?Limites des fonctions réelles
Énoncé
Soit \(f(x)= x-\frac{|x|}{x}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
En utilisant la définition de la valeur absolue, \(f(x)=\left\{\begin{array}{cc}x-1,& \mbox{si} \, \, x > 0 \\ x+1,& \mbox{si} \, x < 0 \end{array}\right.\).
Pour aller plus loin :
?Limites des fonctions réelles
Énoncé
Soit \(f(x)= \frac{x}{|x-1|}-\frac{3x-1}{|x^2-1|}\). Quelles sont les assertions vraies ?
Correction
Explication Générale
En utilisant la définition de la valeur absolue, \(f(x)=\left\{\begin{array}{ccc}\frac{x^2+4x-1}{1-x^2},& \mbox{si} \, x \le -1 \\ \frac{1-x}{1+x} ,& \mbox{si} \, -1\le x \le 1\\ \frac{x-1}{1+x} ,& \mbox{si} \, x \ge 1 \end{array}\right.\)
Pour aller plus loin :
video : Opérations sur les limites
exercices : Limites de fonctions
?Limites des fonctions réelles - limite en un point
Énoncé
Soit \(f(x)= \frac{\sin(3x)}{\sin(4x)}\). Quelles sont les assertions (ou propositions) vraies ?
Correction
Explication Générale
\(\lim_{x\to 0}\frac{\sin x}{x} = 1,\) donc \(\lim_{x\to 0} f(x)= \lim_{x\to 0}\frac{3x}{4x} \cdot \frac{\sin (3x)}{3x}\cdot \frac{4x}{\sin(4x)} = \frac{3}{4}\).
Pour aller plus loin :
video : La fonction sinus
?Limites des fonctions réelles - limite en un point
Énoncé
Soit \(f(x)= xE(\frac{1}{x})\), où \(E\) désigne la partie entière. Quelles sont les assertions (ou propositions) vraies ?
Correction
Explication Générale
Pour tout \(x\in \mathbf{R}\), on a : \(x-1 < E(x)\le x\). Donc \(1-x < f(x) \le 1\), pour \(x > 0\) et \(1 \le f(x) < 1-x\), pour \(x < 0\). On déduit que \(\lim_{x\to 0} f(x) =1\).
Pour aller plus loin :
video : Opérations sur les limites
?Limites des fonctions réelles
Énoncé
Soit \(f\) une fonction définie sur \([0,1]\) par : \(f(x)=\left\{\begin{array}{cc}x-1,& \mbox{si} \, x \in \mathbf{R} \setminus \mathbf{Q}\\ 1,& \mbox{si} \, x \in \mathbf{Q} \end{array}\right.\). Quelles sont les assertions (ou propositions) vraies ?
Correction
Explication Générale
L'ensemble des rationnels est dense dans \(\mathbf{R}\). Donc il existe une suite de rationnels \((u_n)\) qui tend vers \(0\) et donc \(\lim_{n\to +\infty} f(u_n)=1\). D'autre part, l'ensemble des irrationnels est dense dans \(\mathbf{R}\). Donc il existe une suite d'irrationnels \((v_n)\) qui tend vers \(0\) et donc \(\lim_{n\to +\infty} f(v_n)=\lim_{n\to +\infty} (v_n-1) = -1 \). On en déduit que \(f\) n'admet pas de limite en \(0\).
Pour aller plus loin :
cours : Limites et fonctions continues
video : Notion sur les fonctions
video : Densité dans R
exercices : Limites de fonctions
?Limites des fonctions réelles
Énoncé
Soit \(f\) une fonction définie sur \(]0,1[\) par : \(f(x)=1\), si \(x \in \mathbf{R} \setminus \mathbf{Q}\) et \(f(x)=\frac{1}{m},\) si \(x= \frac{n}{m},\) où \(n, m \in \mathbf{N}^*\) tels que \( \frac{n}{m}\) soit une fraction irréductible. Quelles sont les assertions (ou propositions) vraies ?
Correction
Explication Générale
L'ensemble des irrationnels est dense dans \(\mathbf{R}\). Donc il existe une suite d'irrationnels \((u_n)\) qui tend vers \(1^-\) et donc \(\lim_{n\to +\infty} f(u_n)=1\). D'autre part, la suite \((\frac{n}{n+1})\) tend vers \(1^-\) et \(\lim_{n\to +\infty} f(\frac{n}{n+1})=\lim_{n\to +\infty} \frac{1}{n+1} = 0 \). On déduit que \(f\) n'admet pas de limite en \(1^-\).
Pour aller plus loin :
cours : Limites et fonctions continues
video : Notion sur les fonctions
video : Densité dans R
exercices : Limites de fonctions
?Limites des fonctions réelles - étude d'une fonction croissante
Énoncé
Soit \(f:\mathbf{R} \to \mathbf{R}\) une fonction croissante. Quelles sont les assertions (ou propositions) vraies ?
Correction
Explication Générale
(a) On suppose que \(f\) est majorée et on pose \(M=\sup_{x\in \mathbf{R}} f(x)\) (le plus petit des majorants de \(f\)). Alors, \( \lim_{x\to +\infty } f(x)=M\). En effet, soit \(\epsilon > 0\), alors il existe \(a > 0\) tel que : \(M-\epsilon < f(a)\le M \). Comme \(f\) est croissante, si \(x\ge a\), alors \(M-\epsilon < f(a)\le f(x)\le M \). D'où le résultat, d'après la définition d'une limite. (b) On suppose que \(f\) n'est pas majorée. Alors, \( \lim_{x\to +\infty } f(x)=+\infty\). En effet, soit \(A > 0\), alors il existe \(a > 0\) tel que \(f(a) > A\). Comme \(f\) est croissante, si \(x\ge a\), alors \(f(x)\ge f(a) > A\). D'où le résultat, d'après la définition d'une limite.
Pour aller plus loin :
video : Les limites et l'infini
video : Fonctions bornées
?Limites des fonctions réelles - limite en un point
Énoncé
Soit \(f(x)= \frac{\sqrt{x+1}-1}{\sqrt[3]{x+1}-1}\). Quelles sont les assertions (ou propositions) vraies ?
Correction
Explication Générale
On pourra multiplier \(f\) par \(\sqrt{x+1}+1\) et \((\sqrt[3]{x+1})^2+\sqrt[3]{x+1}+1\) les expressions conjuguées de \(\sqrt{x+1}-1\) et de \(\sqrt[3]{x+1}-1\) respectivement. On obtient : \(f(x)=\frac{(\sqrt[3]{x+1})^2+\sqrt[3]{x+1}+1}{\sqrt{x+1}+1}\).
Pour aller plus loin :
exercices : Limites de fonctions
?Limites des fonctions réelles - limite en l'infini
Énoncé
Soit \(f(x)=x+\sqrt[5]{1-x^5}\). Quelles sont les assertions (ou propositions) vraies ?
Correction
Explication Générale
En utilisant l'égalité : \(a^5+b^5=(a+b)(a^4-a^3b+a^2b^2-ab^3+b^4)\), on pourra multiplier \(f\) par l'expression conjuguée de \(x+\sqrt[5]{1-x^5}\). On obtient : \(f(x)=\big[x^4-x^3\sqrt[5]{1-x^5} +x^2(\sqrt[5]{1-x^5})^2-x(\sqrt[5]{1-x^5})^3+(\sqrt[5]{1-x^5})^4\big]^{-1}\).
Pour aller plus loin :
exercices : Limites de fonctions
?Limites des fonctions réelles - limite en l'infini
Énoncé
Soit \(f(x)=\sqrt{x^3+2x^2+3}-ax\sqrt{x+b}, \, a,b \in \mathbf{R}\). \(f\) admet une limite finie en \(+\infty\) si et seulement si :
Correction
Explication Générale
Si \(a\le 0\), \(\lim_{x\to +\infty} f(x)=+\infty\). On suppose donc que \(a > 0\) et on multiplie \(f\) par son expression conjuguée. on obtient : \(f(x)= \frac{(1-a^2)x^3+(2-a^2b)x^2+3}{\sqrt{x^3+2x^2+3}+ax\sqrt{x+b}}\). On déduit que \(f\) admet une limite finie en \(+\infty\) si et seulement si \(a=1\) et \(b=2\).
Pour aller plus loin :
exercices : Limites de fonctions
?Limites des fonctions réelles - limite en un point
Énoncé
Soit \(f\) la fonction définie sur \(]\frac{3}{2}, +\infty[ \setminus \{2\}\) par : \(f(x)=\left\{\begin{array}{cc}a\frac{\sqrt{x-1}-1}{x-2},& \mbox{si} \, x < 2 \\ \frac{\sqrt{2x-3}-b}{x-2},& \mbox{si} \, x > 2 \end{array}\right.\). \(f\) admet une limite finie quand \(x\) tend vers \(2\) si et seulement si :
Correction
Explication Générale
Si \(b\neq 1\), \(f\) admet une limite infinie quand \(x\) tend vers \(2^+\). On suppose que \(b=1\) et on multiplie \(f\) par l'expression conjuguée selon les cas. On obtient : \(f(x)=\left\{\begin{array}{cc} \frac{a}{\sqrt{x-1}+1}& \mbox{si} \, x < 2 \\ \frac{2}{\sqrt{2x-3}+1}& \mbox{si} \, x > 2 \end{array}\right.\). On déduit que \(f\) admet une limite finie quand \(x\) tend vers \(2\) si et seulement si \(a=2\).
Pour aller plus loin :
exercices : Limites de fonctions
?Limites des fonctions réelles - limite en l'infini
Énoncé
Soit \(f(x)=\frac{(2x)^x}{x^{(2x)}}\). Quelles sont les assertions (ou propositions) vraies ?
Correction
Explication Générale
Par définition, si \(u\) et \(v\) sont deux fonctions telles que \(u > 0\), \(u^v=e^{v\ln u}\). On en déduit que \(f(x)=\exp[ x\ln (2x )- 2x\ln x] = \exp[ x\ln 2 - x\ln x]\). Donc \(\lim_{x\to +\infty } f(x)=0\).
Pour aller plus loin :
video : Logarithme Népérien
video : Exponentielle
?Nombres complexes - trigonométrie
Énoncé
Soit \(\theta\) un réel. Quelles sont les assertions vraies ?
Correction
Explication Générale
On peut appliquer les formules de Moivre.
Pour aller plus loin :
?Nombres complexes -trigonométrie
Énoncé
Soit \(\theta\) un réel. Quelles sont les assertions vraies ?
Correction
Explication Générale
On peut appliquer la formule de Moivre.
Pour aller plus loin :
?Nombres complexes - module/argument
Énoncé
Soit \(z=1+ e^{i\theta},\theta \in ]-\pi,\pi[\). Quelles sont les assertions vraies ?
Correction
Explication Générale
\(z=e^{i\frac{\theta}{2}} (e^{i\frac{\theta}{2}} + e^{-i\frac{\theta}{2}}) = 2 \cos (\frac{\theta}{2}) e^{i\frac{\theta}{2}}\). Comme \(\theta \in ]-\pi,\pi[\) , \(\cos (\frac{\theta}{2}) > 0\). On déduit que : \(|z|=2\cos (\frac{\theta}{2})\) et \(\arg z = \frac{\theta}{2} \, [2\pi]\).
Pour aller plus loin :
video : Argument et trigonométrie
?Nombres complexes - module/argument
Énoncé
Soit \(x\in \mathbf{R}\backslash \{2k\pi, k \in \mathbf{Z}\}\), \(n \in \mathbf{N}^*\), \(S_1= \sum_{k=0}^{n} \cos(kx)\) et \(S_2= \sum_{k=0}^{n} \sin(kx)\). Quelles sont les assertions vraies ?
Correction
Explication Générale
On calcule la somme géométrique \(\sum_{k=0}^{n} e^{ikx}= \sum_{k=0}^{n} (e^{ix})^k = \frac{1-e^{i(n+1)x}}{1-e^{ix}}=\frac{e^{i\frac{(n+1)x}{2}}(e^{-i\frac{(n+1)x}{2}}-e^{i\frac{(n+1)x}{2}})}{e^{i\frac{x}{2}}(e^{-i\frac{x}{2}}-e^{i\frac{x}{2}})}= e^{i\frac{nx}{2}}\cdot \frac{\sin (\frac{n+1}{2})x}{\sin (\frac{x}{2})}\); puis, la partie réelle et imaginaire de cette somme.
Pour aller plus loin :
?Nombres complexes - équations
Énoncé
Les racines cubiques de \(1+i\) sont :
Correction
Explication Générale
On résout l'équation : \(z^3=1+i= \sqrt 2e^{i\frac{\pi}{4}}\).
Pour aller plus loin :
video : Argument et trigonométrie
?Nombres complexes - module/argument
Énoncé
Soit \(z\in \mathbf{C}\) tel que \(|z-2|=1\). Quelles sont les assertions vraies ?
Correction
Explication Générale
\(|z-2|=1\), donc \(z-2=e^{i\theta}\), \(\theta \in \mathbf{R}\).
Pour aller plus loin :
video : Nombres complexes et géométrie
?Nombres complexes - équations
Énoncé
On considère l'équation \((E) : \, (z^2+1)^2+z^2=0, \, z\in \mathbf{C}\). L'ensemble des solutions de \((E)\) est :
Correction
Explication Générale
Remarquer que \((z^2+1)^2+z^2= (z^2+1)^2 - (iz)^2= (z^2-iz+1)(z^2+iz+1)\). On peut aussi poser \(Z=z^2\) et se ramener à une équation du second degré.
Pour aller plus loin :
exercices : Nombres complexes
?Suites réelles - limites
Énoncé
Soit \(n \in \mathbb N^*\) et soit \(\displaystyle u_n=n\ln\left(1+\frac{1}{n}\right)\) et \(\displaystyle v_n=\left(1+\frac{1}{n}\right)^n\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On utilise le fait que si \(\displaystyle \lim _{n\to +\infty}a_n=0\), alors les suites \((a_n)\) et \(\ln (1+a_n)\) sont équivalentes. Ainsi le terme \(u_n\) est équivalent, en \(+\infty\), à \(\displaystyle n\times \frac{1}{n}=1\). Donc \(\displaystyle \lim _{n\to +\infty}u_n=1\) et, puisque \(v_n=\mathrm{e}^{u_n}\), \(\displaystyle \lim _{n\to +\infty}v_n=\mathrm{e}\).
Pour aller plus loin :
video : Limite
?Suites réelles - calcul de limites
Énoncé
Soit \(n\) un nombre entier non nul et soit \(\displaystyle u_n=\frac{2^{n+1}-3^{n+1}}{2^n+3^n}\) et \(\displaystyle v_n=\frac{n2^{2n}-3^n}{n2^{2n}+3^n}\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
D'abord, \(\displaystyle u_n=\frac{3^{n+1}\times \left[\left(\frac{2}{3}\right)^{n+1}-1\right]}{3^n\times \left[\left(\frac{2}{3}\right)^{n}+1\right]}=3\frac{\left(\frac{2}{3}\right)^{n+1}-1}{\left(\frac{2}{3}\right)^n+1}\). Or \(\displaystyle \left(\frac{2}{3}\right)^n\) est le terme général d'une suite géométrique de limite \(0\), donc \(\displaystyle \lim _{n\to +\infty}u_n=3\frac{0-1}{0+1}=-3\). De même, \(\displaystyle v_n=\frac{n(2^2)^n-3^n}{n(2^2)^n+3^n}=\frac{n4^n-3^n}{n4^n+3^n}=\frac{n4^n\times \left[1-\frac{1}{n}\left(\frac{3}{4}\right)^{n}\right]}{n4^n\times \left[1+\frac{1}{n}\left(\frac{3}{4}\right)^{n}\right]}=\frac{1-\frac{1}{n}\left(\frac{3}{4}\right)^{n}}{1+\frac{1}{n}\left(\frac{3}{4}\right)^{n}}.\) Donc \(\displaystyle \lim _{n\to +\infty}v_n=1\) car \(\displaystyle \lim _{n\to +\infty}\frac{1}{n}=0\) et\(\displaystyle \lim _{n\to +\infty}\left(\frac{3}{4}\right)^{n}=0\).
Pour aller plus loin :
video : Premières définitions
video : Exemples remarquables
?Suites réelles - étude d'une suite
Énoncé
Soit \(n\in\mathbb {N^*}.\) Soit \(\displaystyle u_n=1+\frac{1}{2^2}+\frac{1}{3^2}+\dots +\frac{1}{n^2}\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On vérifie par récurrence que \(\displaystyle u_n\leq 2-\frac{1}{n}\), donc \((u_n)\) est majorée par \(2\). Par ailleurs, il est clair que \((u_n)\) est croissante. Le théorème des suites monotones implique que \((u_n)\) est convergente et que \(\displaystyle \lim _{n\to +\infty}u_n\leq 2\).
Pour aller plus loin :
video : Théorèmes de convergence
?Suites réelles - étude de la limite
Énoncé
Soit \((u_n)\) une suite réelle. On suppose que \(\displaystyle |u_{n+1}-1|\leq \frac{1}{2}|u_n-1|\) pour tout \(n\geq 0\). Que peut-on en déduire ?
Correction
Explication Générale
On vérifie par récurrence que \(\displaystyle |u_n-1|\leq \frac{1}{2^n}|u_0-1|\), et donc, par passage à la limite, \(\displaystyle \lim _{n\to +\infty}(u_n-1)=0\). C'est-à-dire, \(\displaystyle \lim _{n\to +\infty}u_n=1\).
Pour aller plus loin :
video : Limite
?Suites réelles - étude d'une suite
Énoncé
Soit \(n\) un nombre entier non nul et soit \(\displaystyle u_n=\left|\frac{1}{n}-\frac{2}{n}+\frac{3}{n}-\dots+\frac{(-1)^{n-1}n}{n}\right|\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On vérifie que, pour tout \(n\geq 1\), \(u_{2n}=\frac{1}{2}\mbox{ et }u_{2n+1}=\frac{n+1}{2n+1}.\) Donc les suites \((u_{2n})\) et \((u_{2n+1})\) convergent vers la même limite, à savoir \(\displaystyle \frac{1}{2}\). D'après le théorème des suites extraites, la suite \((u_n)\) converge aussi vers \(\displaystyle \frac{1}{2}\).
Pour aller plus loin :
video : Théorèmes de convergence
?Suites réelles - étude de la convergence
Énoncé
Soit \(n\) un entier supérieur ou égal à 1. On considère les suites de termes généraux \(\displaystyle u_n=\sum _{k=1}^n\frac{(-1)^k}{k}\), \(\displaystyle v_n=\sum _{k=1}^{n}\frac{(-1)^{2k}}{2k}\) et \(\displaystyle w_n=\sum _{k=1}^{2n+1}\frac{(-1)^{2k+1}}{2k+1}\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On vérifie que \((v_n)\) est décroissante, \((w_n)\) est croissante et que \(\displaystyle \lim _{n\to +\infty}(v_n-w_n)=0\). Donc ces deux suites sont adjacentes. En particulier, elles convergent et elles ont la même limite \(\ell \in \mathbf{R}\). Or \(v_n=u_{2n}\) et \(w_n=u_{2n+1}\), donc, d'après le théorème des suites extraites, la suite \((u_n)\) converge aussi vers \(\displaystyle \ell\).
Pour aller plus loin :
?Suites réelles - étude d'une suite définie par récurrence
Énoncé
Soit \(a > 0\). On définit par récurrence une suite \((u_n)_{n\geq 0}\) par \(u_0 > 0\) et, pour \(n\geq 0\), \(\displaystyle u_{n+1}= \frac{u_n^2+a^2}{2u_n}\). Que peut-on en déduire ?
Correction
Explication Générale
Par récurrence, \(u_n > 0\) pour tout \(n\in \mathbf{N}\). Donc \((u_n)\) est bien définie. D'autre part, \(\displaystyle 0\leq (u_n-a)^2=u_n^2+a^2-2au_n \Rightarrow a\leq \frac{u_n^2+a^2}{2u_n}.\) Donc \(u_{n+1}\geq a > 0\) pour tout \(n\in \mathbf{N}\). On en déduit que \(\displaystyle u_{n+1}-u_n=\frac{a^2-u_n^2}{2u_n}\leq 0,\mbox{ pour }n\geq 1,\) donc \((u_n)_{n\geq 1}\) est décroissante. On vérifie aussi par récurrence que \(\displaystyle \left|u_{n+1}-a\right|\leq \frac{\left|u_1-a\right|}{2^n}\), et donc, par passage à la limite, \(\displaystyle \lim _{n\to +\infty}(u_n-a)=0\). C'est-à-dire, \((u_n)\) est convergente et \(\displaystyle \lim _{n\to +\infty}u_n=a\).
Pour aller plus loin :
video : Premières définitions
video : Limite
?Suites réelles - étude d'une suite croissante
Énoncé
Soit \((u_n)\) une suite croissante. On suppose que \(\displaystyle u_{n+1}-u_n\leq \frac{1}{2^n}\) pour tout \(n\geq 0\). Que peut-on en déduire ?
Correction
Explication Générale
On vérifie par récurrence que \(\displaystyle u_0\leq u_n\leq u_0+1+\frac{1}{2}+\frac{1}{2^2}+\dots +\frac{1}{2^{n-1}}=u_0+2-\frac{1}{2^{n-1}}.\) Donc, \(u_0\leq u_n\leq u_0+2\). Étant à la fois croissante est majorée, la suite \((u_n)\) est convergente et, par passage à la limite, \(\displaystyle u_0\leq \lim _{n\to +\infty}u_n\leq u_0+2\).
Pour aller plus loin :
video : Premières définitions
video : Limite
video : Théorèmes de convergence
?Suites réelles - étude d'une suite définie par récurrence
Énoncé
Soit \((u_n)_{n\geq 0}\) la suite définie par \(u_0\geq 0\) et \(\displaystyle u_{n+1}= \ln(1+u_n)\). Que peut-on en déduire ?
Correction
Explication Générale
On vérifie par récurrence que \(\displaystyle 0\leq u_n\) pour tout \(n\geq 0\). Donc la suite \((u_n)\) est bien définie. On vérifie aussi que \(\ln (1+x)\leq x\) pour tout réel \(x\geq 0\). En particulier, \(u_{n+1}=\ln (1+u_n)\leq u_n.\) Donc \((u_n)\) est décroissante. Étant à la fois décroissante est minorée, la suite \((u_n)\) est convergente et sa limite est l'unique solution de l'équation \(x=\ln (1+x)\). Soit \(\displaystyle \lim _{n\to +\infty}u_n=0\).
Pour aller plus loin :
video : Suites récurrentes
?Suites réelles - étude d'une suite croissante
Énoncé
Soit \((u_n)\) une suite croissante. On suppose que \(\displaystyle 0\leq u_{n+1}\leq \frac{1}{2}u_n+\frac{1}{2^n}\) pour tout \(n\geq 0\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
On vérifie par récurrence que, pour tout \(n\geq 1\), \(\displaystyle 0\leq u_n\leq \frac{1}{2^n}u_0+1+\frac{1}{2}+\frac{1}{2^2}+\dots +\frac{1}{2^{n-1}}=\frac{1}{2^n}u_0+2-\frac{1}{2^{n-1}}.\) Donc, \((u_n)\) est majorée car \(\displaystyle \frac{1}{2^{n-1}}\underset{+\infty}{\longrightarrow}0\). \'Etant à la fois croissante est majorée, la suite \((u_n)\) converge vers \(\ell \in \mathbf{R}\) et, par passage à la limite, \(\displaystyle 0\leq \ell\leq 2\). Par ailleurs, l'hypothèse faite sur \(u_n\) donne \(0\leq \ell \leq \frac{\ell}{2} \Rightarrow \ell =0\) et comme \((u_n)_{n\geq 1}\) est croissante positive, \(u_n=0\) pour tout \(n\geq 1\).
Pour aller plus loin :
video : Premières définitions
video : Limite
?Suites réelles - étude d'une suite croissante
Énoncé
Soit \((u_n)\) une suite croissante. On suppose que \(\displaystyle u_n+\frac{1}{n+1}\leq u_{n+1}\) pour tout \(n\geq 0\). On remarque que \(u_0+1+\frac{1}{2}+...+\frac{1}{n}.\) Quelles sont les bonnes réponses ?
Correction
Explication Générale
On vérifie par récurrence que, pour tout \(n\geq 1\), \(\displaystyle u_0+1+\frac{1}{2}+\dots +\frac{1}{n}\leq u_n.\) Donc, \((u_n)\) n'est pas majorée car sinon, il en serait de même pour la suite de terme général \(\displaystyle v_n=1+\frac{1}{2}+\dots +\frac{1}{n}\) et on sait que \(\displaystyle \lim _{n\to +\infty}v_n=+\infty\).
Pour aller plus loin :
video : Premières définitions
video : Limite
?Suites réelles - étude d'une suite
Énoncé
On admet que \(\forall x \in [0,1[\), \(\ln (1+x)\leq x\leq -\ln (1-x)\). Soit \(\displaystyle u_n=\sum _{k=1}^n\frac{1}{n+k}\), \(n\geq 1\). Quelles sont les bonnes réponses ?
Correction
Explication Générale
Avec \(\displaystyle x=\frac{1}{n+k}\), on aura : \(\ln(n+k+1)-\ln (n+k)\leq \frac{1}{n+k}\leq \ln(n+k)-\ln (n+k-1).\) On somme sur \(k\) de \(1\) à \(n\), on obtient : \(\ln \left(\frac{2n+1}{n+1}\right)\leq u_n\leq \ln (2n)-\ln (n)=\ln (2).\) Le théorème d'encadrement implique que \((u_n)\) converge et que sa limite est \(\ln (2)\).
Pour aller plus loin :
video : Premières définitions
?Intégrales et primitives
Énoncé
Déterminer \(\int \ln(\sqrt{x})\,dx\).
Correction
Explication Générale
\(\begin{eqnarray*}\int \ln(\sqrt{x})\,dx&=&\int\ln(x^{1/2})\,dx\\&=& \int\frac{1}{2}\ln(x)\,dx\\&=&\frac{1}{2}\int\ln(x)\,dx\end{eqnarray*}\)
Posons \(u(x)=\ln(x)\) et \(v'(x)=1\) alors \(u'(x)=\frac{1}{x}\) et \(v(x)=x\).
En intégrant par parties, on a donc :
\(\begin{eqnarray*}\int\ln(x)\,dx&=&\int u(x) v'(x)\,dx\\&=&[u(x)v(x)]-\int u'(x)v(x)\,dx\\&=&[x\ln(x)]-\int \frac{1}{x}\times x\,dx\\&=&[x\ln(x)]-\int\,dx\\&=&[x\ln(x)]-[x]\\&=&x\ln(x)-x+C\end{eqnarray*}\)
D'où \(\int \ln(\sqrt{x})\,dx=\frac{x\ln(x)}{2}-\frac{x}{2}+C, C\in\mathbb{R}\).
?Intégrales et primitives
Énoncé
Déterminer \(\int (\ln x)^2\,dx\).
Correction
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Une étagère en équilibre, tenue par un fil, subit une force de tension \(\overrightarrow T\) .
Cette étagère est inclinée d'un angle α par rapport à l'horizontale comme le montre la figure ci-dessous.
Quelle est la composante horizontale de \(\overrightarrow T\)?
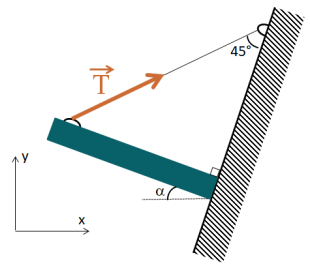
Correction
Explication Générale
Raisonnement : On recherche d'abord la valeur absolue de la grandeur recherchée en raisonnant dans un triangle rectangle bien choisi, puis on détermine le signe ensuite.
Schéma : On commence par dessiner un triangle rectangle dont l'hypoténuse est \(\vec T\) et dont l'un des côtés de l'angle droit est parallèle à l'horizontale : \(T_x\)
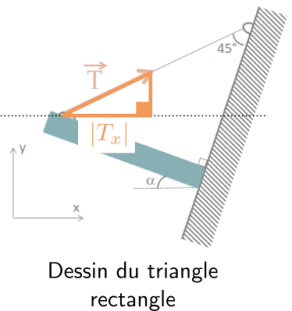
Angles : On ne connaît pas les mesures des angles non droit de ce triangle. On va donc utiliser les angles remarquables de la figure :
On repère deux angles semblables (alterne-interne) :
La droite horizontale qui contient le côté horizontal du triangle que l'on a tracé (et donc qui porte \(\overrightarrow{T_x}\))
La droite horizontale qui définit l'angle \(\alpha\) fait par l'étagère avec l'horizontale.
L'angle entre le fil qui maintient l'étagère et l'étagère est de mesure \(\pi-\pi/2-\pi/4=\pi/4\)
On en déduit que l'angle \(\beta\) entre le fil et l'horizontale est donc de mesure : \(\beta=\frac{\pi}{4}-\alpha\)
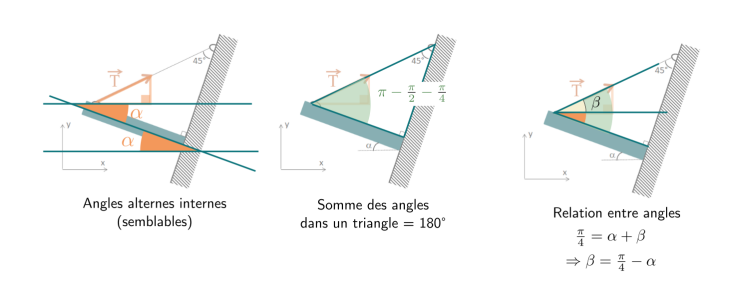
Projection :
Le côté recherché est un côté adjacent à l'angle connu, on utilise donc le cosinus : \(\cos(45°- \alpha)=\frac{|T_x|}{||\vec T||}\)
On isole la grandeur recherchée : \(|T_x|=||\vec T||\cos(45°-\alpha)\)
On détermine le signe : \(\vec T\) est orienté vers la droite, on a donc : \(T_x=+||\vec f||\cos(\alpha-45)\)
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Un objet ponctuel en mouvement circulaire uniforme subit une accélération \(\overrightarrow a\) inclinée d'un angle θ par rapport à l'horizontale à un instant donné.
Quelles sont les composantes du vecteur vitesse \(\overrightarrow V\) qui est orthogonal au vecteur \(\overrightarrow a\)?
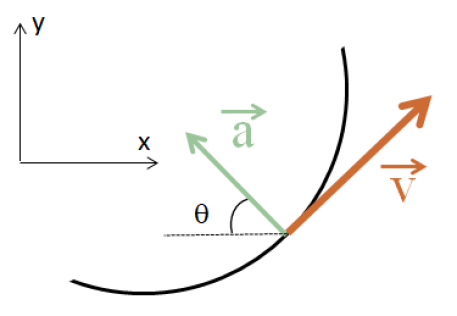
Correction
Explication Générale
Raisonnement : On recherche d'abord la valeur absolue de la grandeur recherchée en raisonnant dans un triangle rectangle bien choisi, puis on détermine le signe ensuite.
Schéma : On commence par dessiner un triangle rectangle dont l'hypoténuse est \(\vec V\)
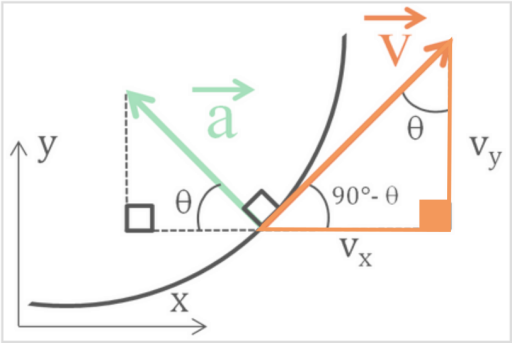
Angles : Les vecteurs accélération et vitesse sont orthogonaux (angle 90°). L'angle du vecteur vitesse par rapport à l'axe horizontal on passe par la somme des angles d'un angle plat \(\pi=\theta + \frac{\pi}{2}- Angle inconnu\) donc \(angle inconnu = 90°-\theta\)
\(V_x\) est le côté opposé à l'angle \(\theta\) du triangle rectangle dessiné ci-dessous.
Donc \(\frac{V_x}{V} = \sin\theta\) soit \(V_x = V \sin \theta\)
\(V_y\) est le côté adjacent à l'angle \(\theta\) du triangle rectangle dessiné ci-dessous.
Donc \(\frac{V_y}{V} = \cos\theta\) soit \(V_y = V \cos \theta\)
Ici \(V_x\) et \(V_y\) sont tous les deux dans le même sens que l'axe horizontale et verticale, ils sont donc positif.
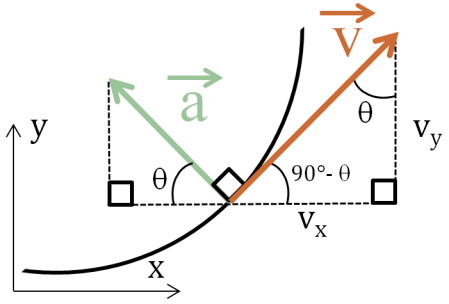
?Exprimer une grandeur à partir d'une relation vectorielle
Énoncé
Un objet ponctuel en mouvement circulaire uniforme subit une accélération \(\overrightarrow a\) inclinée d'un angle θ par rapport à l'horizontale à un instant donné.
Quelles sont les composantes du vecteur vitesse \(\overrightarrow V\) qui est orthogonal au vecteur \(\overrightarrow a\)?
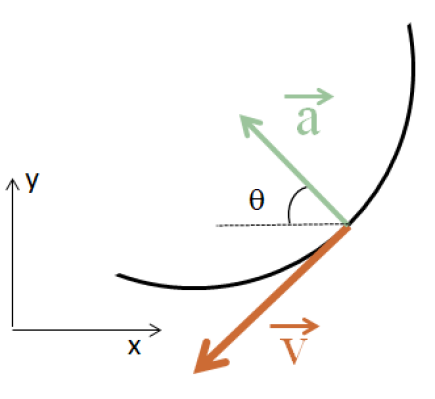
Correction
Explication Générale
Raisonnement : On recherche d'abord la valeur absolue de la grandeur recherchée en raisonnant dans un triangle rectangle bien choisi, puis on détermine le signe ensuite.
Schéma : On commence par dessiner un triangle rectangle dont l'hypoténuse est \(\vec V\)
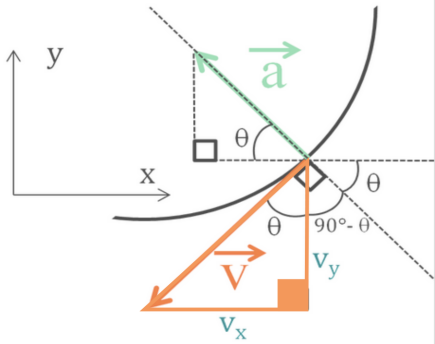
Angles : Les vecteurs accélération et vitesse sont orthogonaux (angle 90°) donc l'angle du vecteur vitesse par rapport à l'axe horizontal est \(90° -\theta\).
\(V_x\) est le côté opposé à l'angle \(\theta\) du triangle rectangle dessiné ci-dessous.
Donc \(\frac{V_x}{V} = \sin\theta\) soit \(V_x = V \sin \theta\)
\(V_y\) est le côté adjacent à l'angle \(\theta\) du triangle rectangle dessiné ci-dessous.
Donc \(\frac{V_y}{V} = \cos\theta\) soit \(V_y = V \cos \theta\)
Ici \(V_x\) est dans le sens opposé de l'axe horizontale, il est donc négatif.
Donc \(V_x = - V \sin \theta\)
ici \(V_y\) est dans le sens opposé de l'axe verticale, il est donc négatig.
Donc \(V_y = - v \cos \theta\)